Envolvente e Involutas
Dada una familia de curvas (o de rectas) de características comunes, se denomina envolvente a aquella curva que es tangente a todas las curvas de la familia en puntos distintos. En relación con ella, cada una de las curvas (o rectas) originales se denominan involutas de la curva envolvente.
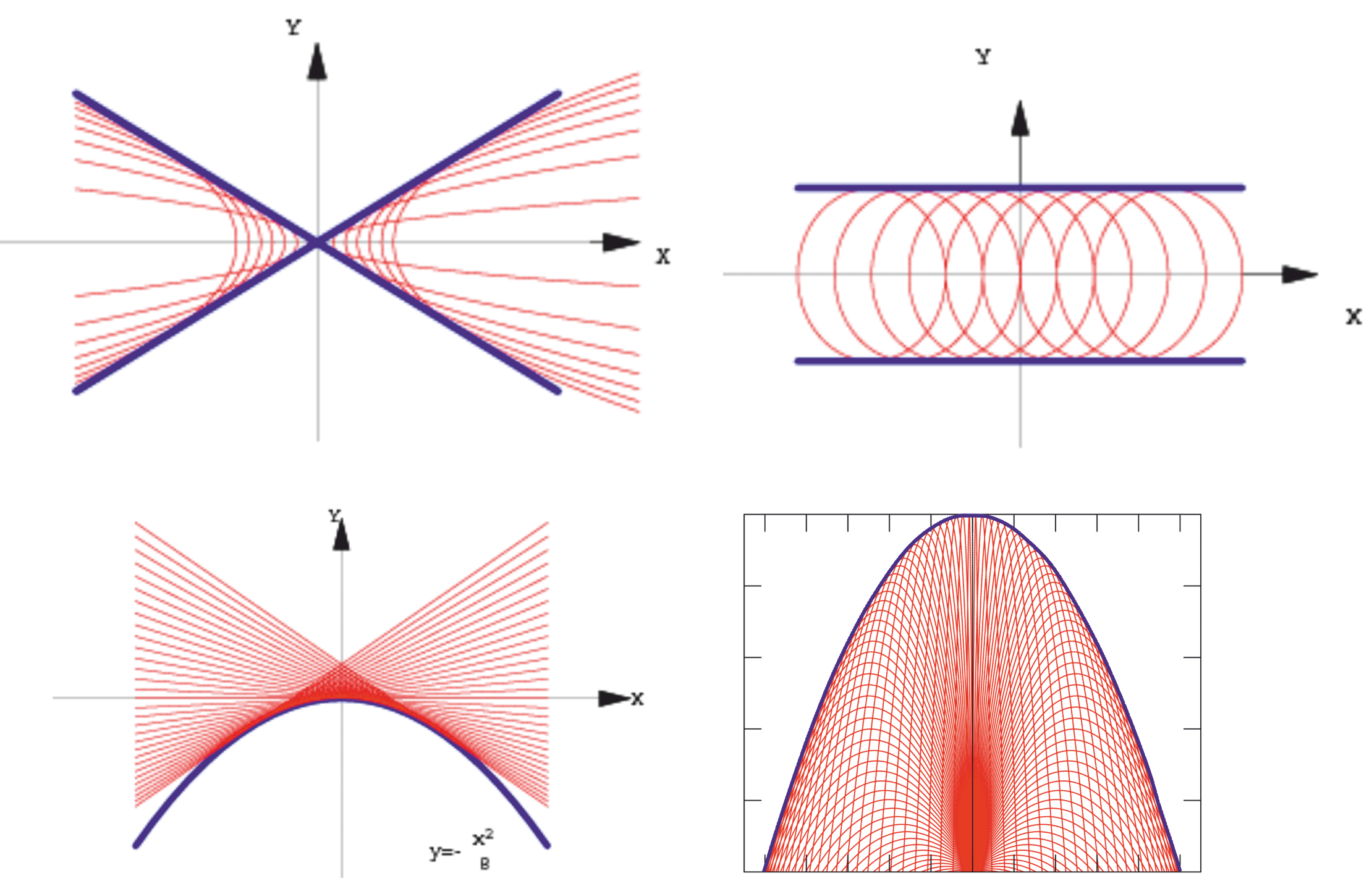
Abajo, Curva envolvente a rectas y curva envolvente a curvas.
Evolvente y Evoluta
Si tenemos una curva c y trazamos en cada uno de sus puntos sus tangentes, hay una curva con respecto a la cual esas rectas son perpendiculares o normales. Esta curva se llama evolvente de la curva c. En relación a ella, la curva original c se denomina evoluta de éstas.
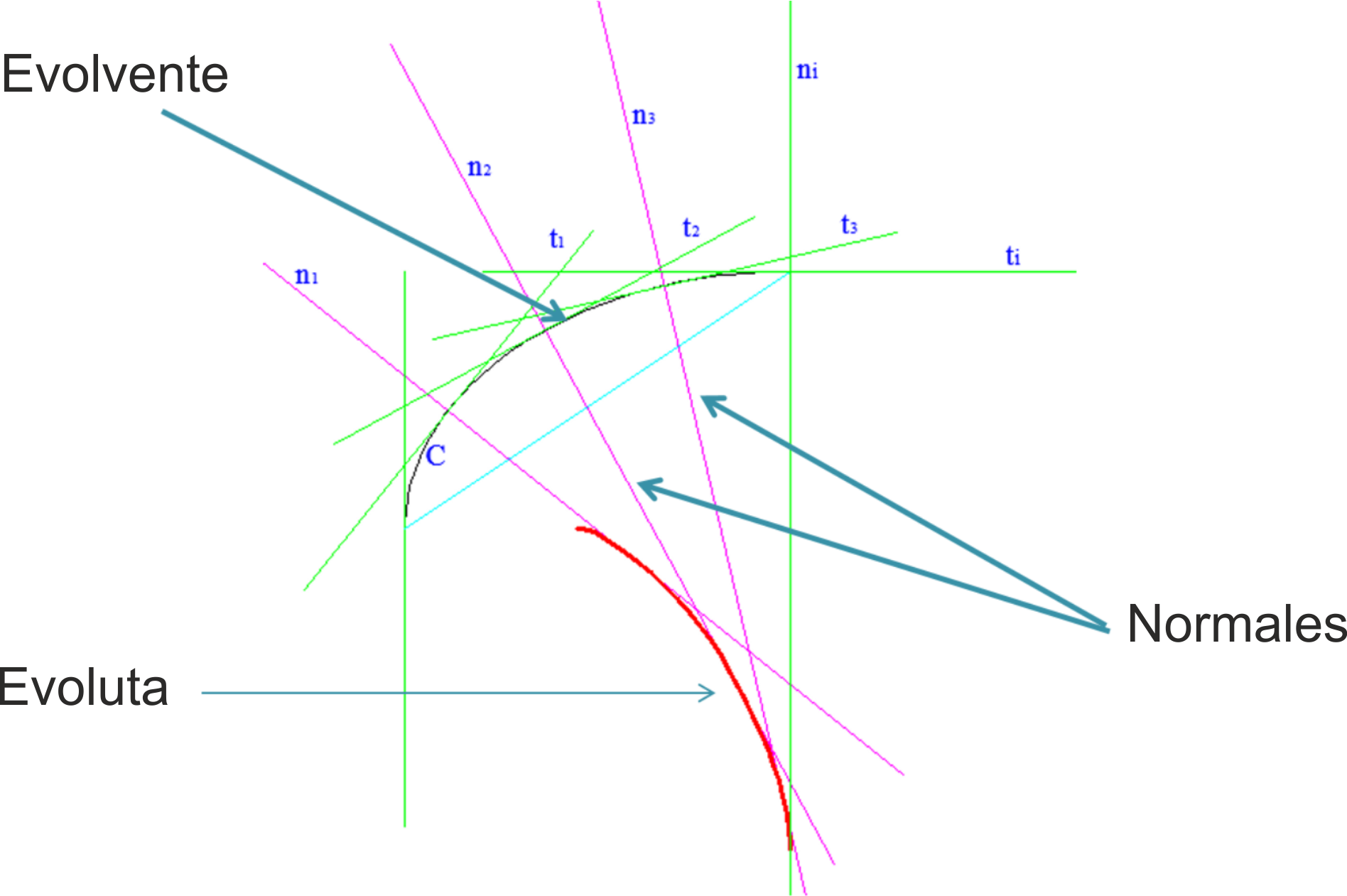
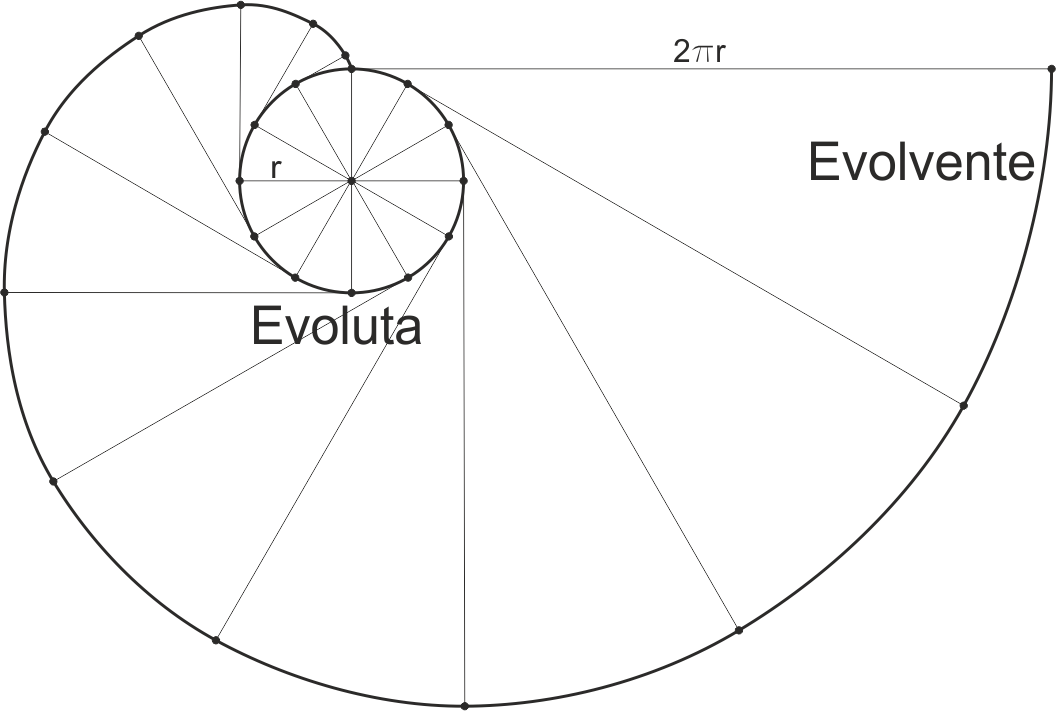
En el caso de una circunferencia, la evolvente es una curva cuyas normales son las tangentes a la circunferencia.
Esta evolvente tiene ciertas propiedades; entre ellas, que si hacemos rodar una línea recta sin deslizamiento sobre una circunferencia, un punto de ella describe una evolvente.
Para trazar la evolvente, podemos aproximarla como la unión de varios arcos, con centros en los puntos de tangencia de la evoluta (cuantas más divisiones hagamos, más exacta es la aproximación).
Hélice cilíndrica
Una hélice es una curva espacial que describe una trayectoria giratoria y que va cambiando de altura. Si la pendiente es constante la curva recorre la superficie de un cilindro, la hélice se denomina cilíndrica.
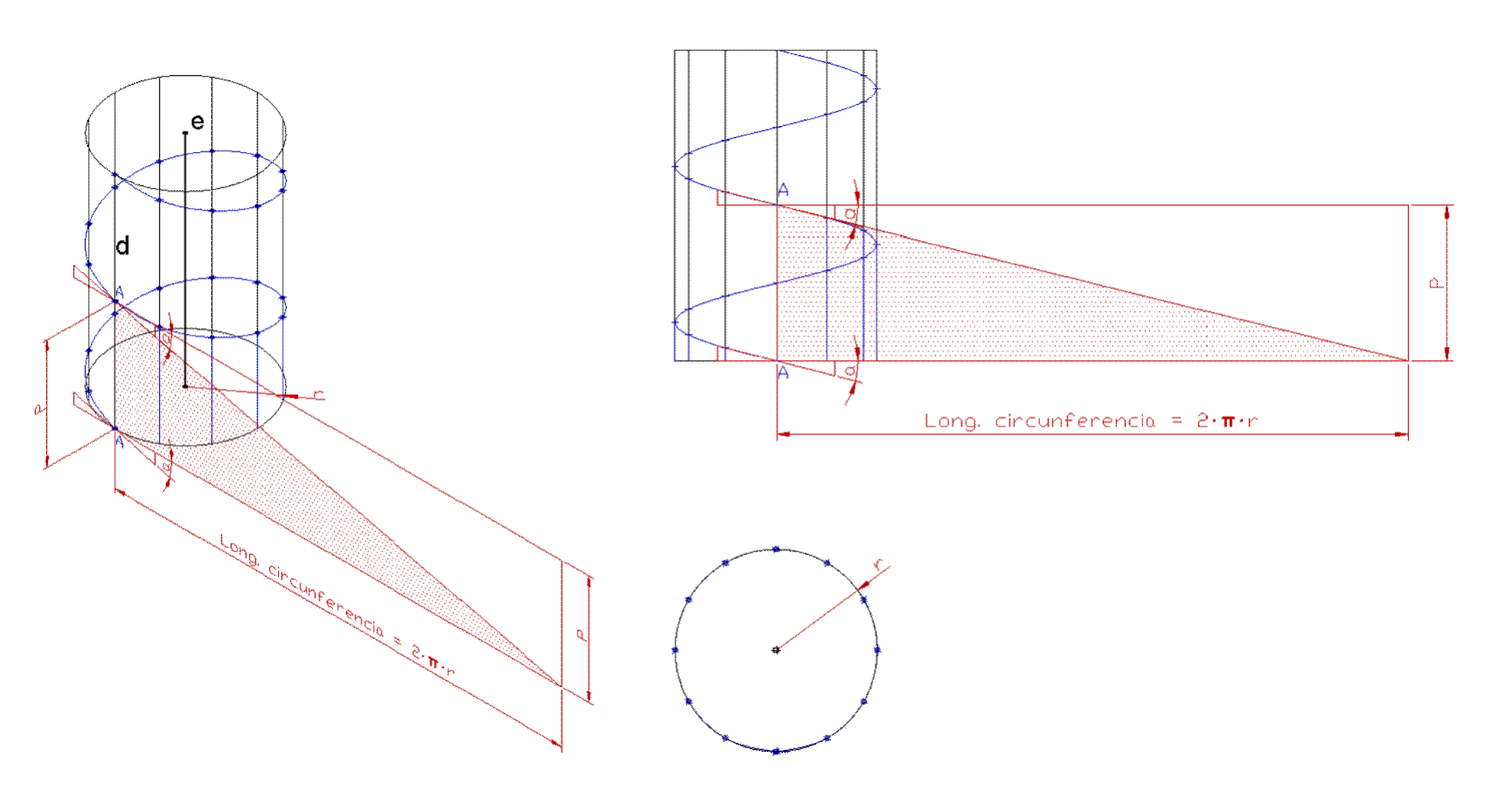
La proyección de una hélice cilíndrica es, como puede verse, un círculo. Si trazamos las rectas tangentes espaciales a la hélice cilíndrica, las proyecciones de estas tangentes son tangentes a su vez al círculo proyectado, y las trazas de estas tangentes forman la evolvente del círculo. En la figura anterior, se ha trazado la tangente a la hélice justo al final de la primera vuelta. Si desarrollamos la curva en esa vuelta, su longitud es la misma que la de la circunferencia proyección.
Helicoide desarrollable
La curva espacial formada por todas las tangentes a una hélice se denomina helicoide. En el caso de la hélice cilíndrica de pendiente constante, el helicoide es desarrollable. Su traza es precisamente la evolvente del círculo que corresponde a la proyección del cilindro (ver capítulo anterior).
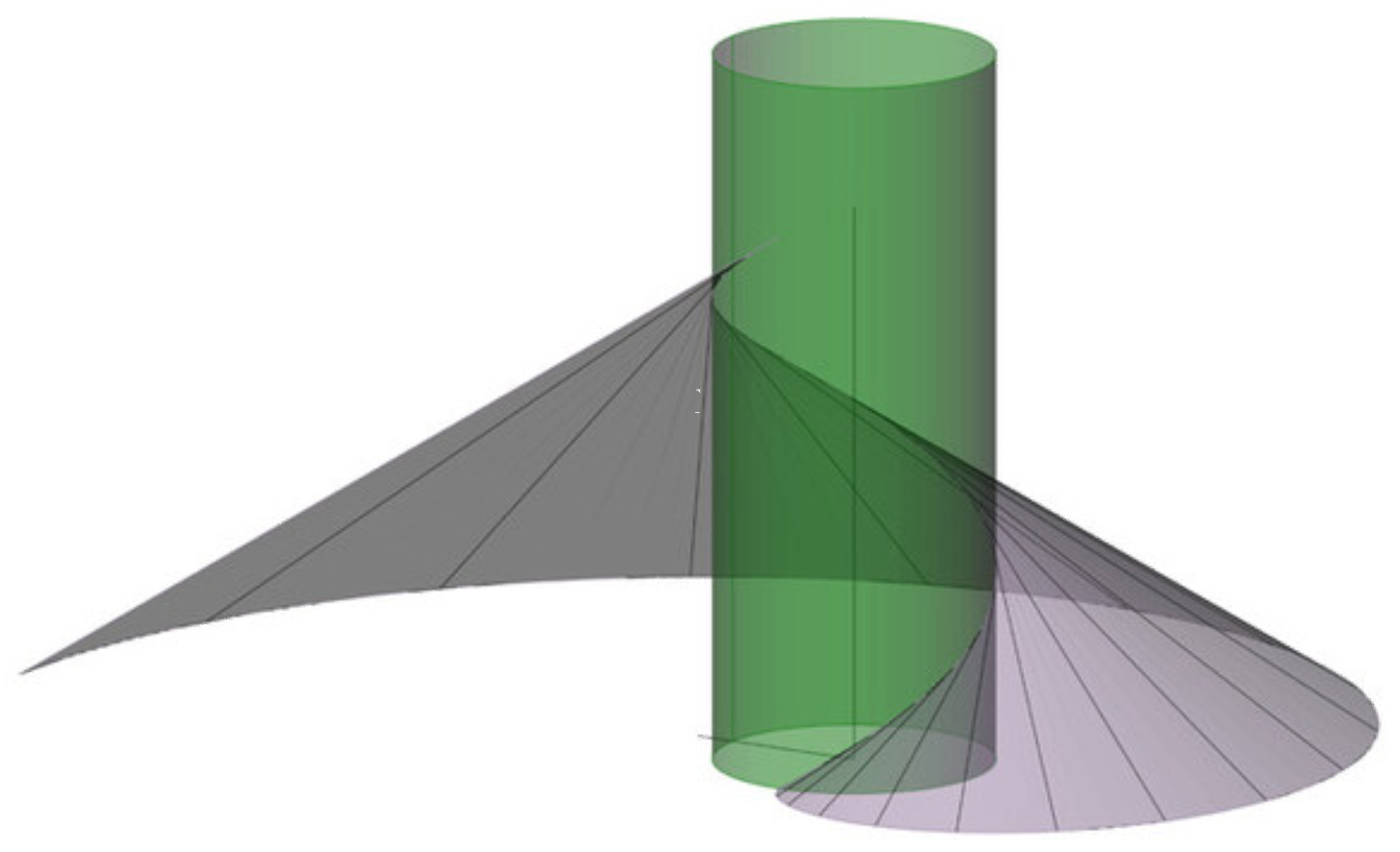
En todas las superficies desarrollables, las generatrices son tangentes a una curva llamada arista de retroceso. En el caso del helicoide la arista de retroceso es la hélice.
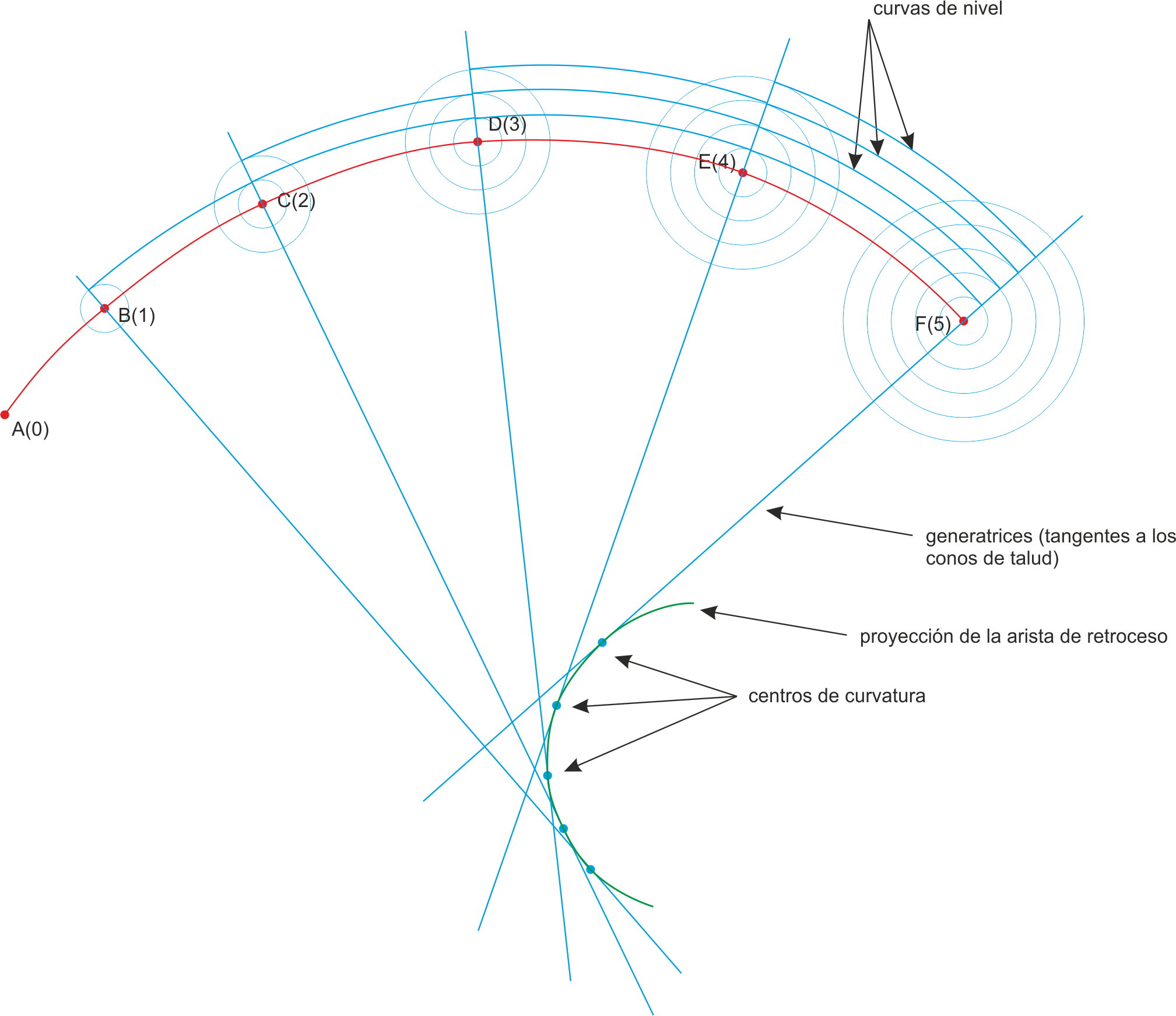
La pendiente de la arista de retroceso (en el espacio) es la misma que presentan las generatrices de la superficie. La proyección de la arista de retroceso es una curva que contiene todos los centros de curvatura de las líneas de nivel. Como conclusión, una superficie desarrollable (distinta a un cono o un cilindro) es una superficie en la cual todos los puntos tienen igual pendiente, y sus generatrices son tangentes a una curva espacial denominada arista de retroceso de la superficie.
La proyección de la arista de retroceso es la evoluta de las curvas de nivel, y esa propiedad la aprovecharemos para su trazado, como se explica más adelante.
Como resumen:
- Las generatrices son normales a las líneas de nivel y tangentes a la arista de retroceso.
- La arista de retroceso es envolvente de las generatrices (y estas son involutas de la a.r.).
- Las líneas de nivel son envolventes de la arista de retroceso (y esta es evoluta de aquellas)
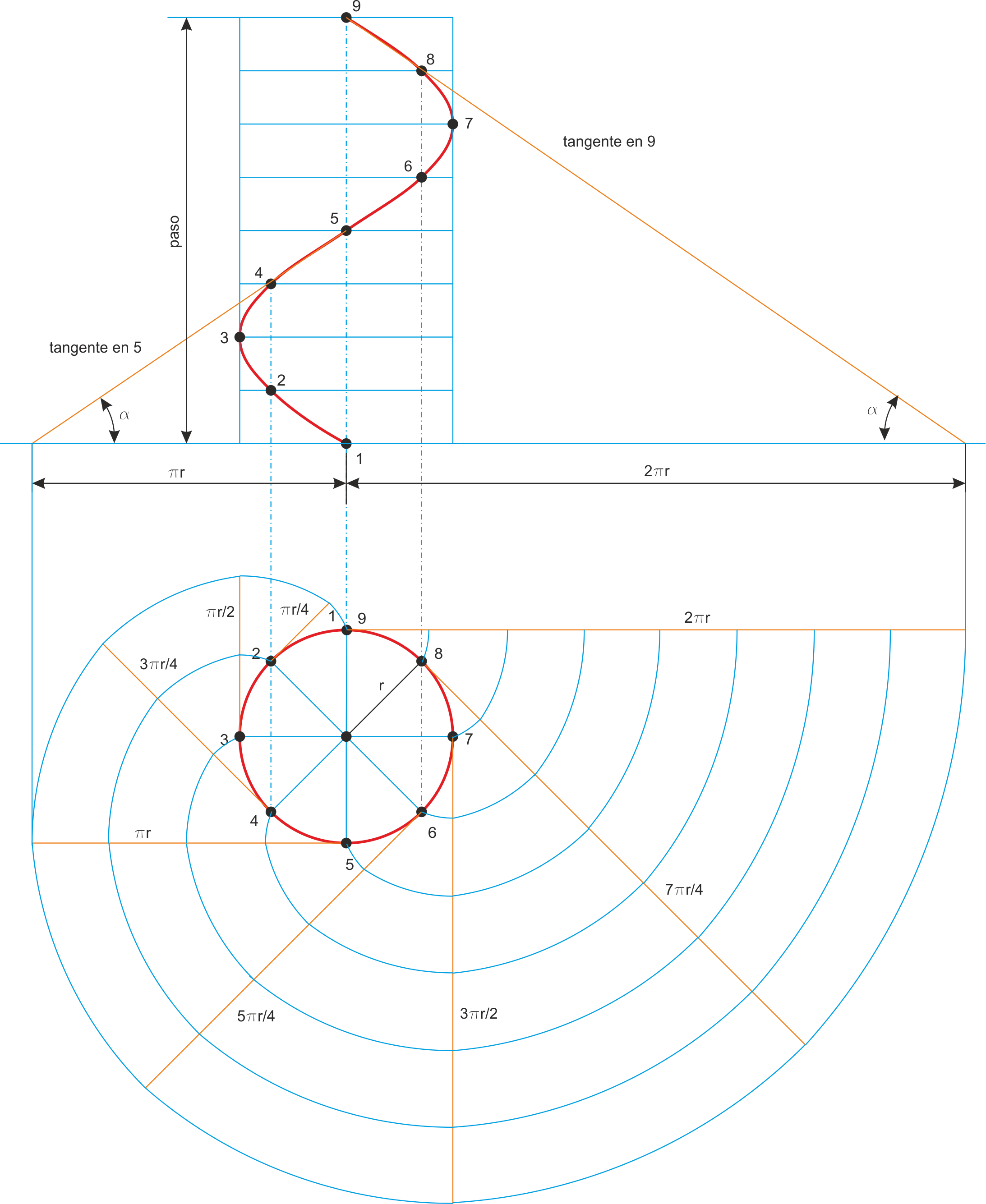
En la figura siguiente se muestra una hélice cilíndrica en alzado y planta. Se ha representado un hilo (un paso) de la hélice, y en la planta se muestran las líneas de nivel del helicoide desarrollable que parte de ella. La pendiente (el ángulo a) depende del paso (altura de una vuelta de la hélice) y del radio del cilindro. Estas líneas de nivel son envolventes del círculo proyección del cilindro, y se han trazado por el método simplificado de tomar como centros los diferentes puntos (1…9) y dibujar arcos de circunferencia tangentes entre sí (podemos calcular las longitudes de las tangentes, cuyos valores se indican en la figura).
Consideremos ahora un cilindro recto coaxial al anterior, de mayor radio (r2), y veamos su intersección con el helicoide anterior. Esta intersección también es una hélice cilíndrica.
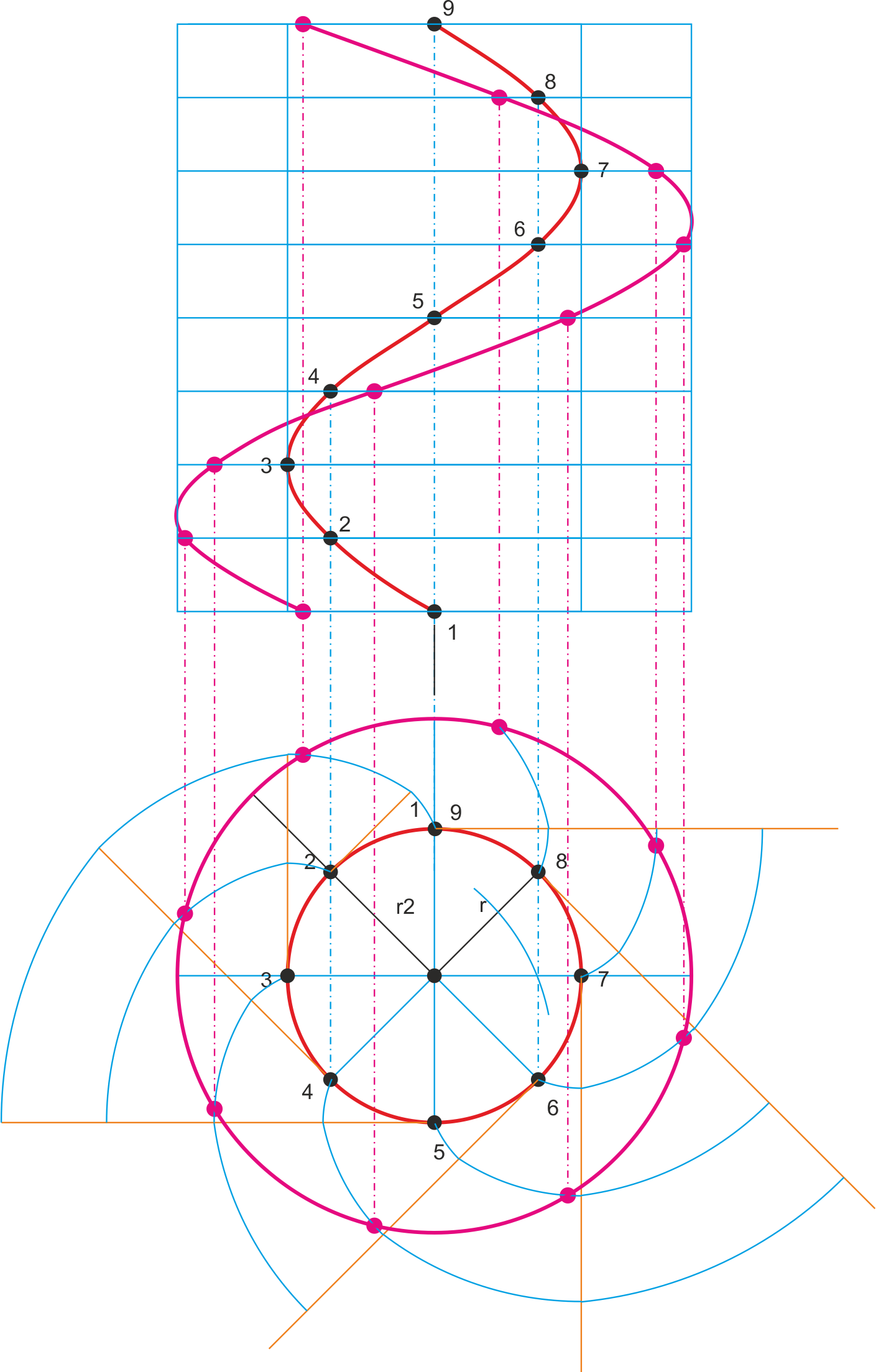
Para la primera hélice se cumple:
Pendiente P1 = DH / L = H / 2pr (pendiente de cualquiera de las tangentes por uno de sus puntos)
Para la segunda hélice:
Pendiente P2= DH2 / L2 = H / 2pr2
Si igualamos despejando H y eliminando 2p, tenemos:
P * r = P2 * r2
Esto nos hace deducir que, si tenemos un talud de contorno circular de radio y pendientes conocidos, podemos calcular cual es la hélice (denominada hélice del núcleo) que, actuando como evoluta (arista de retroceso) puede generar unas evolventes que corresponden a las líneas de nivel del talud.
Ejemplo
Sea una carretera de contorno circular de radio 20 m que asciende desde un punto A(10) hasta un punto E(14), en el extremo de un arco de 120º en el sentido contrario a las agujas del reloj. Se desea una pendiente de talud del 50% (0,5).
Primero, encontramos la pendiente de la hélice del contorno de la carretera:
P = DH / L = 4 /(2p20120/360) = 0,0954 (9,54%)
Ahora encontramos el radio de la hélice del núcleo (proyección de la arista de retroceso):
R2 = RP1/P2 = 20 *0,0954 / 0,5 = 3,816 m
El intervalo de los taludes es i = 1 / 0,5 = 2 m
Por los puntos extremos e intermedios del contorno trazamos las tangentes al círculo del núcleo. Estas tangentes son las líneas de pendiente del talud, así que sobre ellas podemos llevarnos arcos con radio igual al intervalo del talud para marcar los puntos de tangencia de las líneas de nivel (no es necesario).
Para trazar las curvas de nivel (evolventes del círculo del núcleo), hemos hecho una aproximación aprovechando el mecanismo para trazar la evoluta de la circunferencia, pero para minimizar el error hemos tomado como centros de los arcos los puntos intermedios a los centros de curvatura marcados en la arista de retroceso.
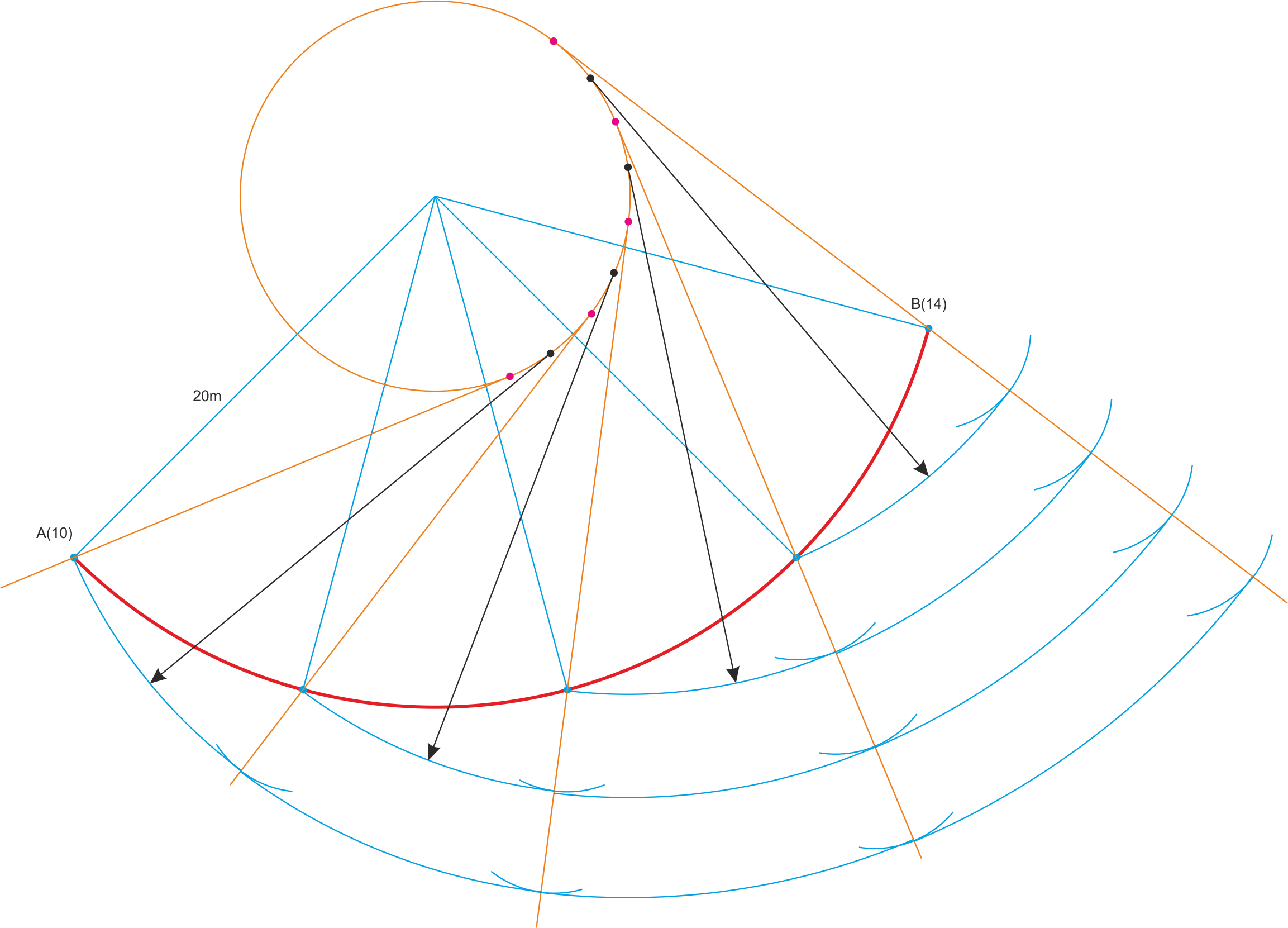
Taludes de planta circular y pendiente constante. La helicoide desarrollable como superficie de talud.
En los tramos circulares (arcos) que no son horizontales, pero que tienen pendiente constante ascendente o descendente, encontramos que la trayectoria que siguen los vértices de los conos de talud es una curva espacial, concretamente una hélice cilíndrica (ver apartados anteriores de este capítulo).
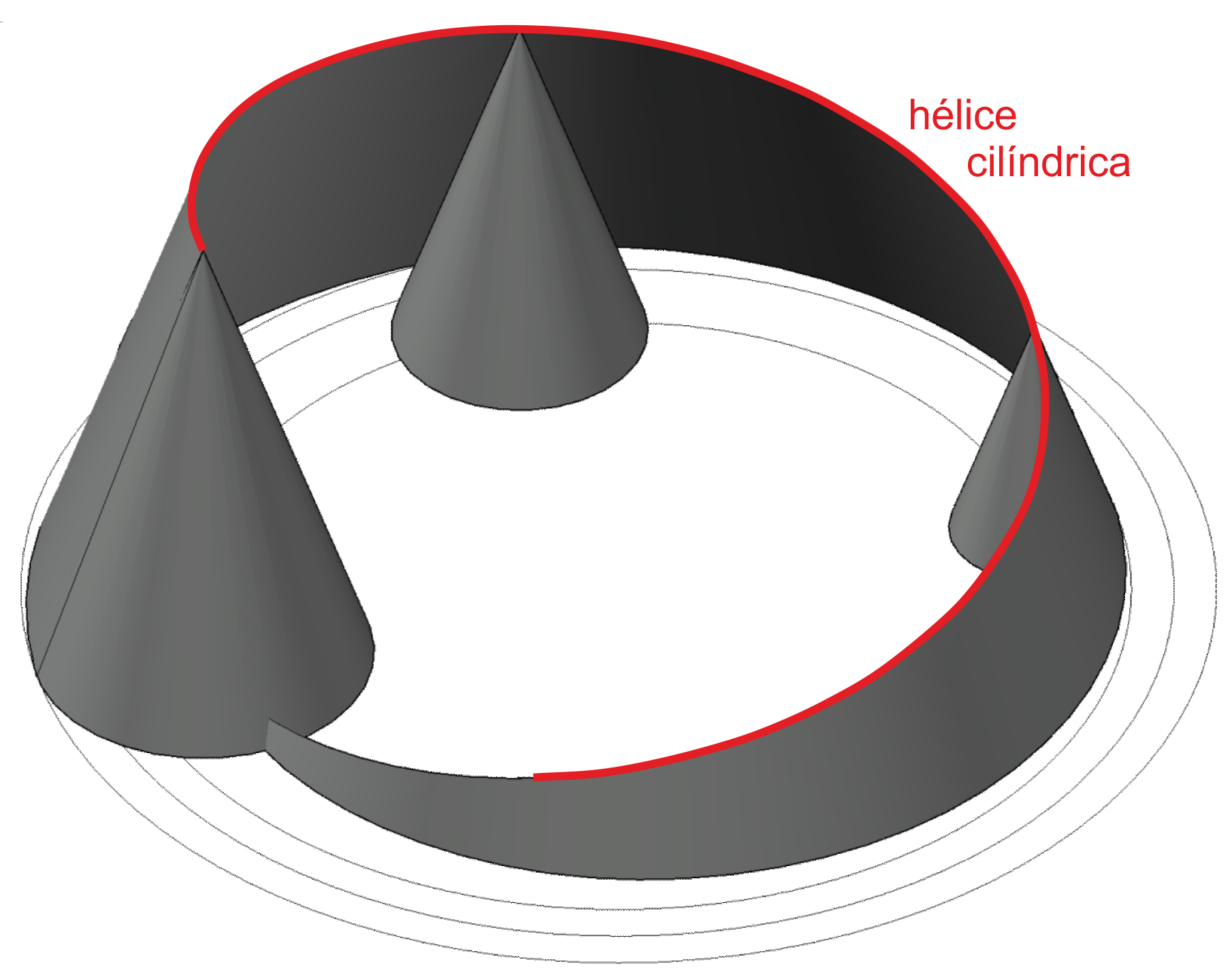
La superficie curva tangente a los conos de talud es una envolvente denominada helicoide desarrollable. En la vista en planta, las líneas de nivel de esta superficie son curvas planas horizontales envolventes a los círculos de igual cota de los conos de talud.
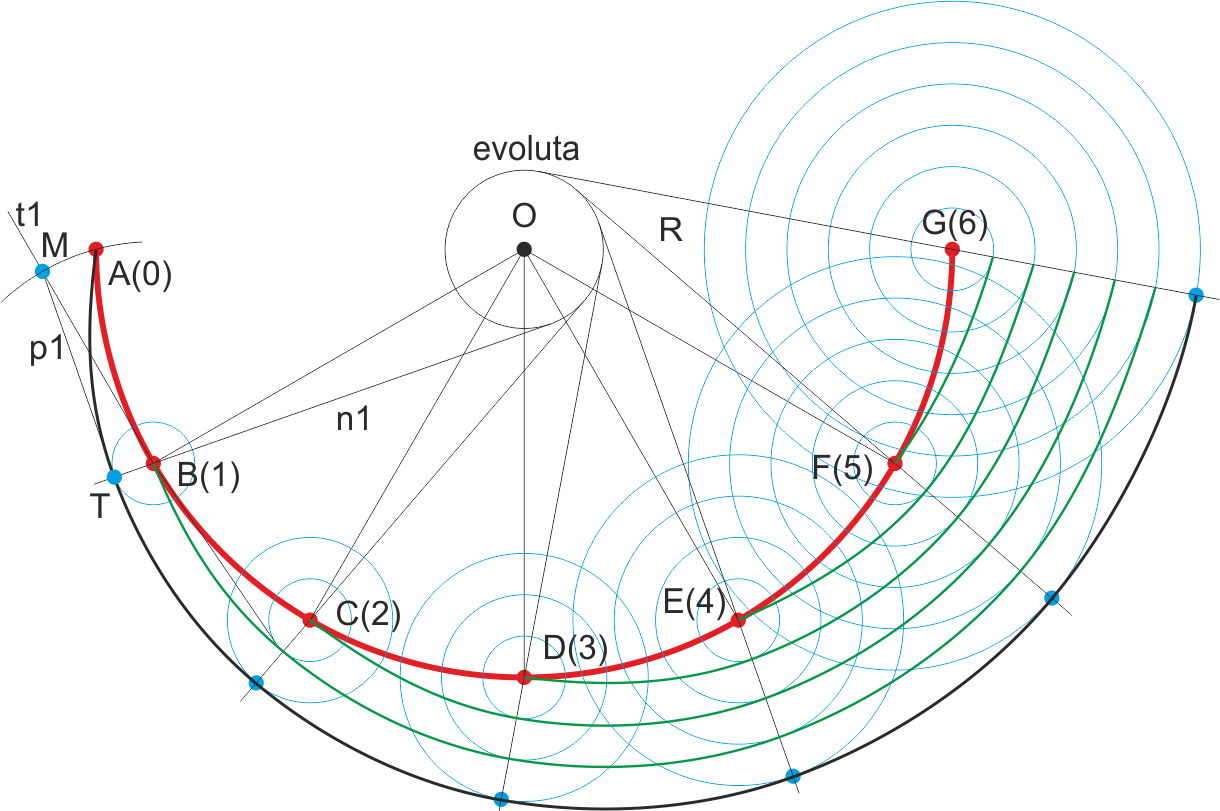
En la figura anterior, el arco AG es el contorno semicircular de un camino que tiene una pendiente constante ascendente desde A(0) hasta G(6). La trayectoria AG (en el espacio) es una hélice cilíndrica cuyo eje se proyecta en el punto O.
El talud que origina es un helicoide desarrollable, que ya hemos visto que tiene pendiente constante en todos sus puntos. Para trazarlo convenientemente, seguimos este procedimiento:
Dividimos el arco AG para encontrar los puntos intermedios (en este caso, por comodidad, los de cota entera). Si por cada uno de ellos trazamos círculos de radio 1m hasta 6 m (m es el módulo o intervalo de la superficie de talud), estos círculos representan los conos de talud. La curva tangente exterior (envolvente) es la línea de nivel de cota 0 del talud (hay dos soluciones, una interior y otra exterior, en la figura solo hemos calculado una). En la figura, es la línea negra más gruesa.
Las curvas tangentes (envolventes) a los círculos de cotas iguales son las diferentes líneas de nivel de la su-perficie del talud (en la figura, las líneas verdes). Estas envolventes son a su vez evolventes de una circunferencia (evoluta), lo que nos ayudará a su trazado. Vamos a encontrarla.
Trazamos la tangente a la curva por el punto B (t1). Sobre ella buscamos el punto M, rectificando la curva AB. Como es una distancia pequeña (cuanto más pequeños sean los arcos, más precisión), aproximamos esa rectificación directamente trazando un arco con centro en B y radio BA.
Por el punto M trazamos una tangente (p1) a la circunferencia base del cono de talud del punto B, obteniendo el punto de tangencia T. Como sabemos que la curva que vamos a obtener es una evolvente, existirá un círculo (evoluta) tal que todas sus tangentes definirán la curva. Por T trazamos una recta n1 perpendicular a p1 (esta es una normal a la evolvente que estamos buscando). Esta recta será tangente a la circunferencia evoluta (con centro en O), así que podemos encontrarla y trazarla.
Una vez tengamos la circunferencia evoluta (que es la proyección de una hélice cilíndrica), bastará con trazar tangentes sucesivas por los puntos C, D, E, F y G para encontrar los puntos de tangencia en las líneas de nivel de todos los conos de talud. Con esos puntos se trazan todas las líneas de nivel del talud (como arcos).
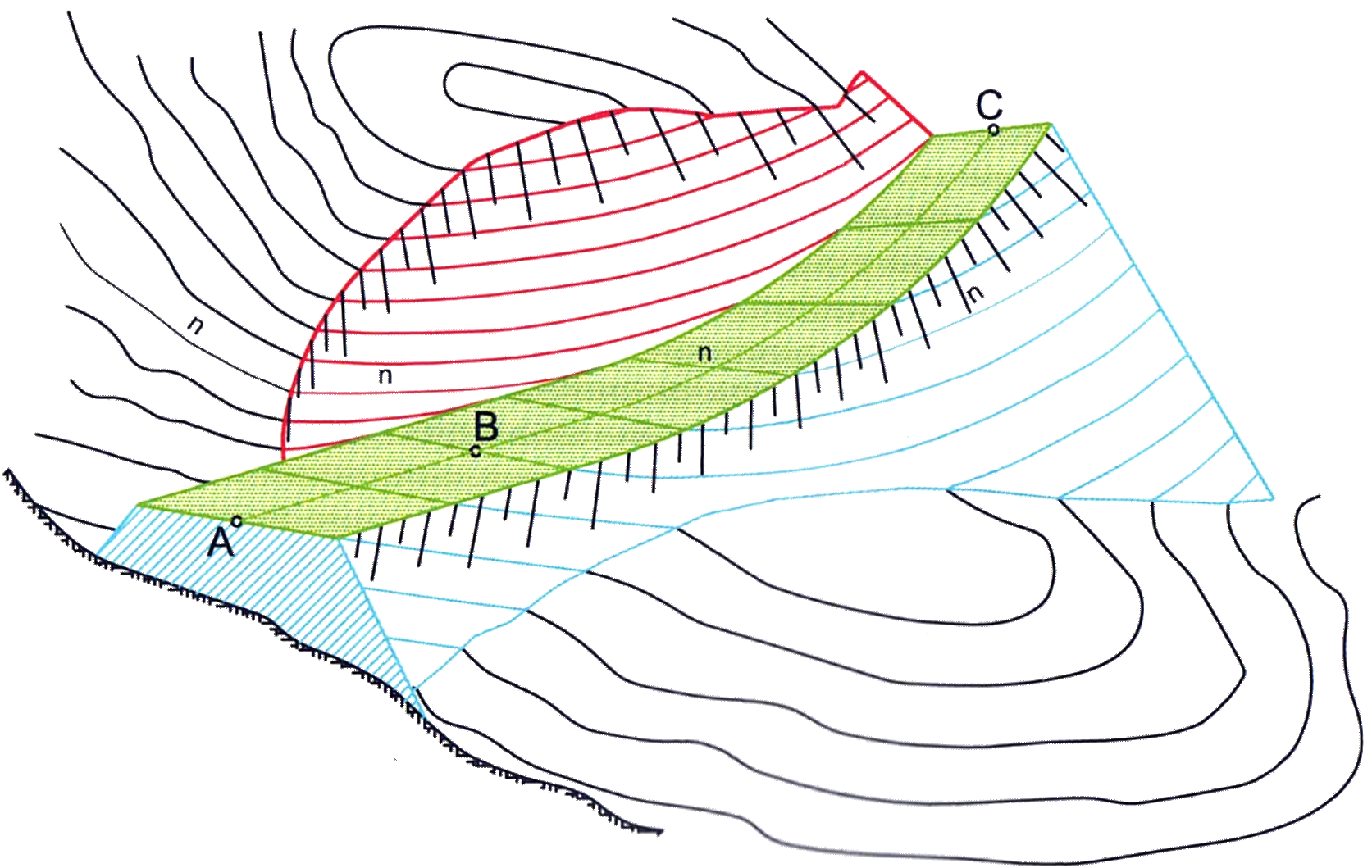
Talud en plataforma de contorno elíptico
Si el contorno de la plataforma es elíptico, hay que tener en cuenta que las líneas de nivel no son elipses.
La arista de retroceso es la evoluta de la elipse.
Recordemos que en una elipse la normal es la bisectriz de los radiovectores, y la tangente es su perpendicular:
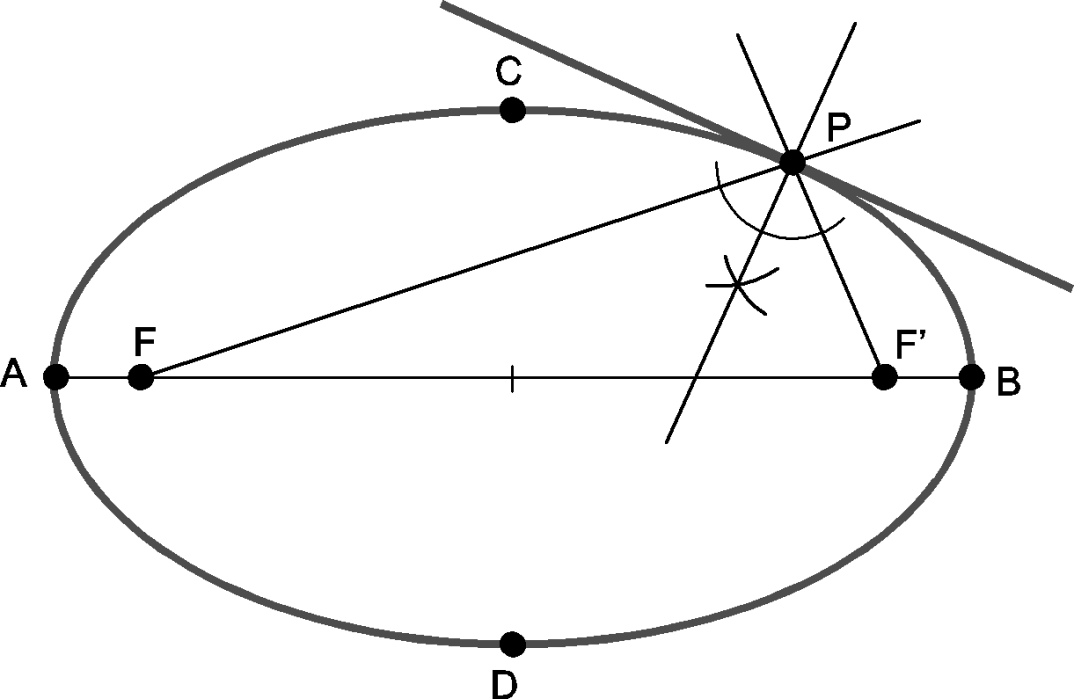
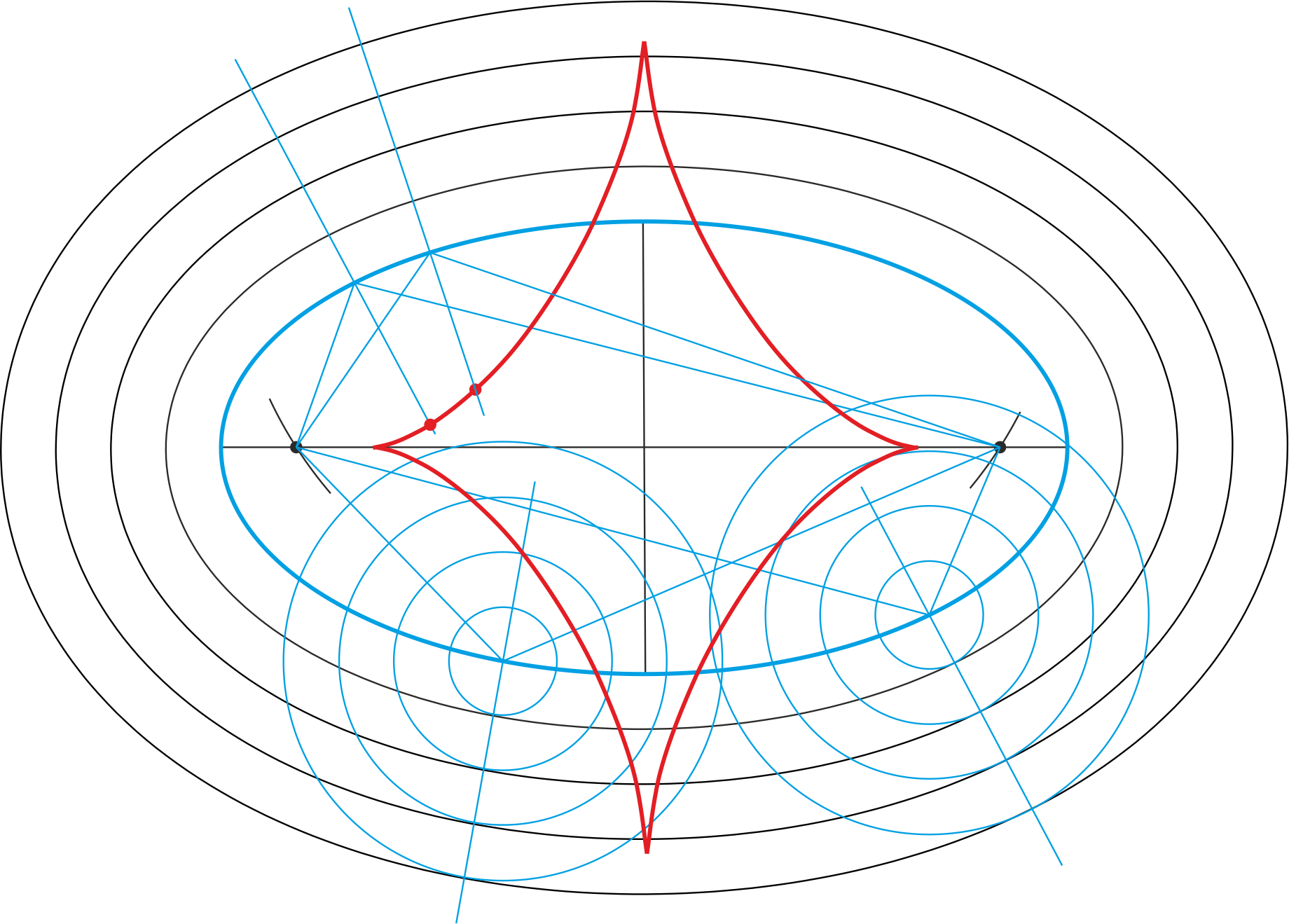
La evoluta de la elipse es una curva en cuatro segmentos denominada astroide tricúspide. Para trazarla, en el cuadrante AB hemos tomado 4 puntos y hemos encontrado las normales. Para los extremos de la curva, hemos trazado la perpendicular por C al segmento AB. Se ha repetido por simetría a los otros tres cuadrantes.

La evoluta es la arista de retroceso tanto de la elipse como de las curvas de nivel equidistantes.
Recordatorio
Al resolver cualquier ejercicio en el que estén implicados desmontes y terraplenes, sea cual sea el tipo de plataforma, es indispensable calcular de forma previa las líneas de paso, ya que sus extremos en el contorno de la plataforma definen donde empiezan y terminan los desmontes y los terraplenes.
Hay que analizar cada una de las partes en que queda dividido el contorno por una línea de paso, decidir si se aplica un terraplén o un desmonte, y calcularlo aplicando las pendientes que se hayan definido en cada caso.
Si las pendientes de desmonte y terraplén son diferentes, en los casos que sea necesario habrá que calcular y trazar dos aristas de retroceso diferentes.
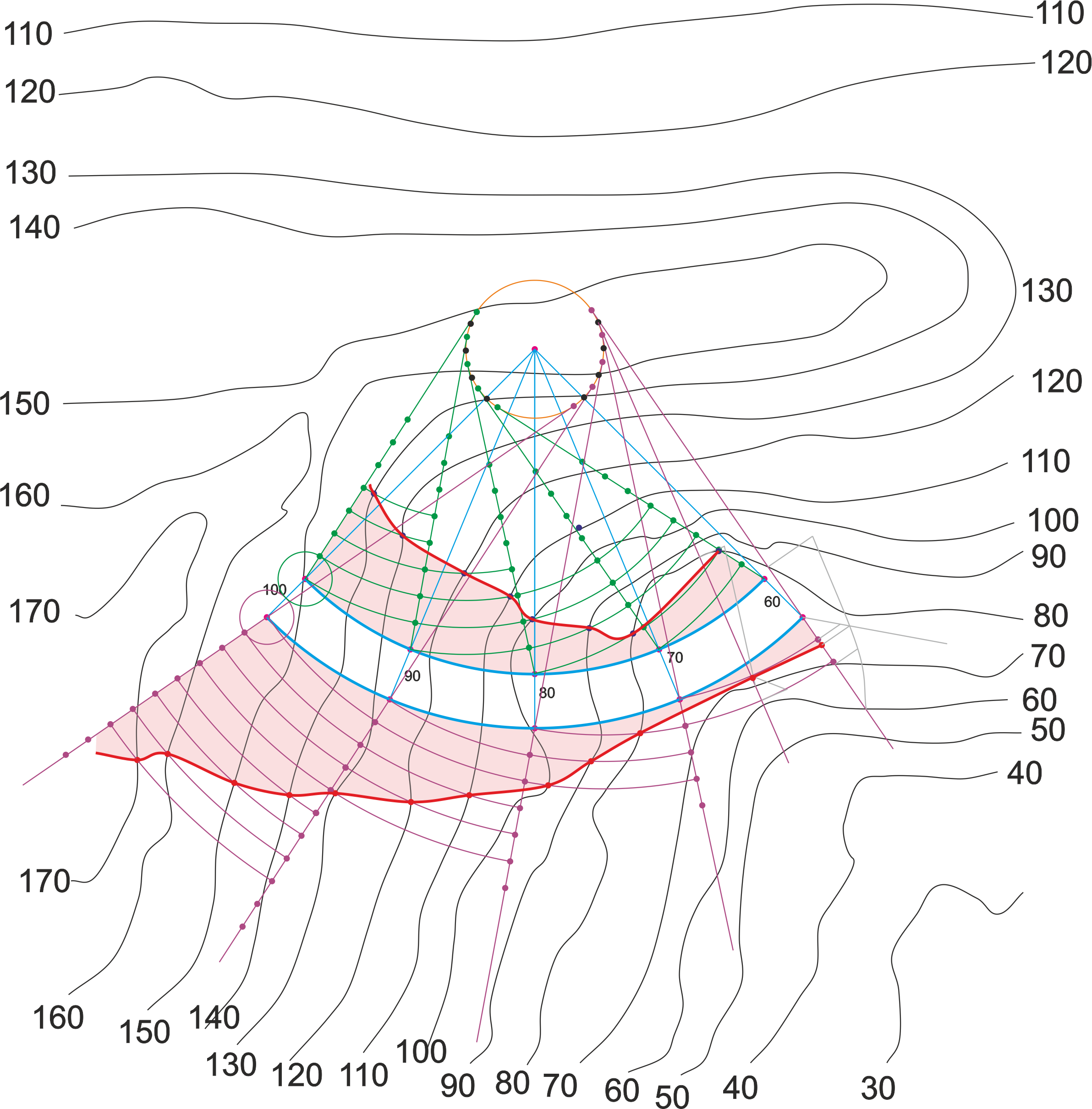
Caso práctico
Curva de proyección circular y pendiente constante, sin línea de paso. La curva describe 90º. Pendientes de desmonte y terraplén al 100%. Escala 1:2000. Arco exterior radio 140 m, arco interior radio 120 m (ancho 20 m).
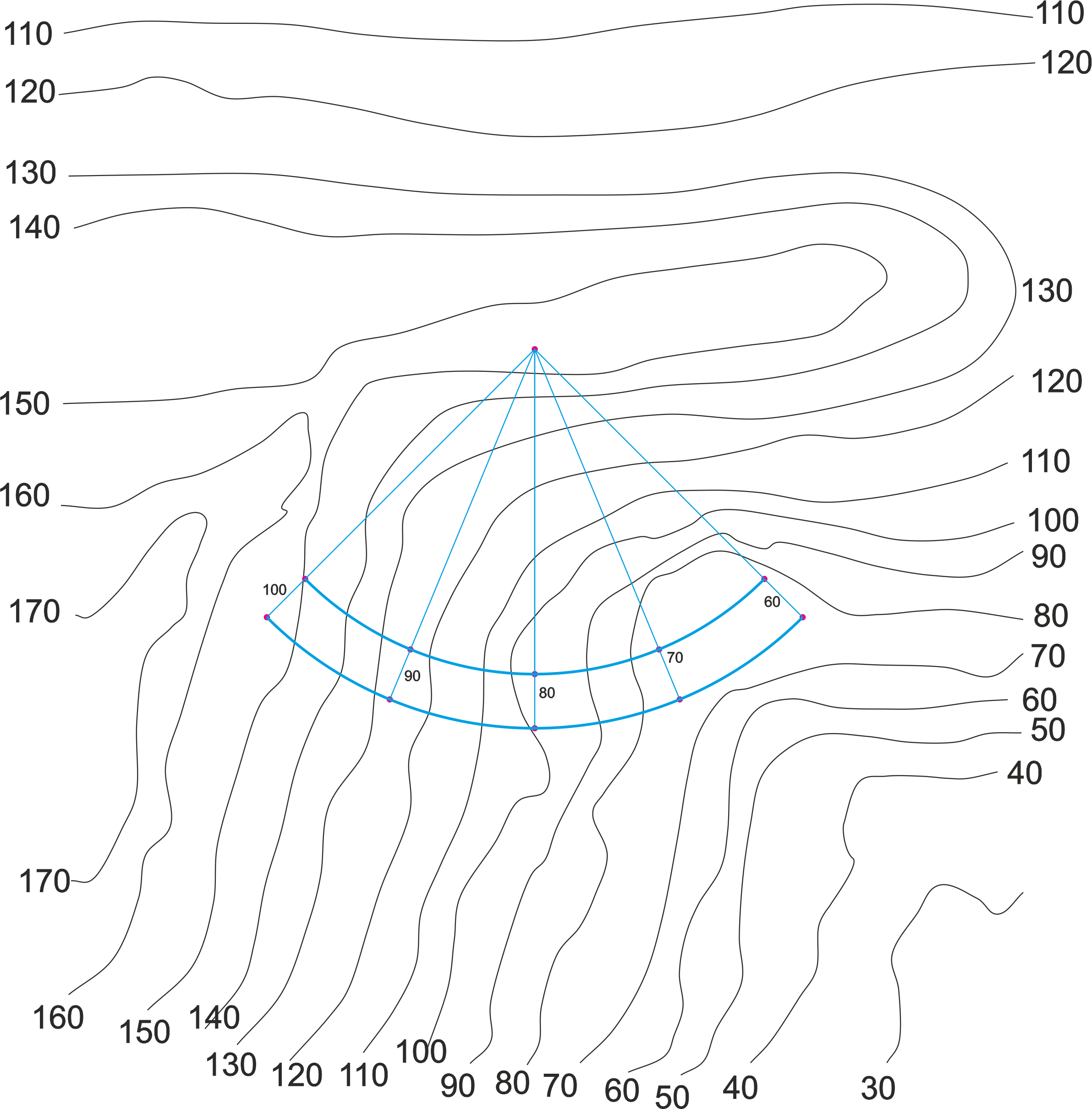
Analizando los contornos, podemos comprobar que solo habrá desmonte, a ambos lados del camino.
Como se trata de un tramo curvo de pendiente constante, vamos a resolverlo por el método del helicoide desarrollable. Calcularemos dos aristas de retroceso, una para cada borde del camino. En este caso, como las pendientes de desmonte son iguales, deberíamos obtener la misma arista de retroceso en ambos casos.
Empezamos a resolver la ladera inferior. La pendiente del contorno es:
Pc1= DH / (2 * Prc1 * ¼) = 40 / (2 * 3,1416 * 140 * ¼) = 0,18189 (18,19%)
Sabemos que
Rar1 = Pc1 * RC1 / Par.
La pendiente de la arista de retroceso es 1, que es la pendiente que va a tener el talud.
Como sabemos que ParRar = PcRc, calculamos Rar1 (radio de la arista de retroceso 1), que da 25,46 m.
Hagamos el mismo cálculo para el contorno superior:
Pc2 = DH / (2* Prc2 * ¼) = 40 / (2 * 3,1416 * 120 * ¼) = 0,2122 (21,22%)
Calculamos Rar2 = Pc2 * RC2 / Par, lo que da también 25,46 m. Es evidente que el valor del radio de la arista de retroceso es independiente del radio de la curva, y que solo va a depender del ángulo y del paso. Hemos obtenido la misma arista de retroceso para ambos lados del camino.
Ya podemos trazar las líneas de pendiente en ambos lados (tangentes a la arista de retroceso). Debemos tener cuidado en discernir hacia qué lado debemos lanzar las tangentes para que las líneas de nivel tengan coherencia con el desmonte o terraplén.
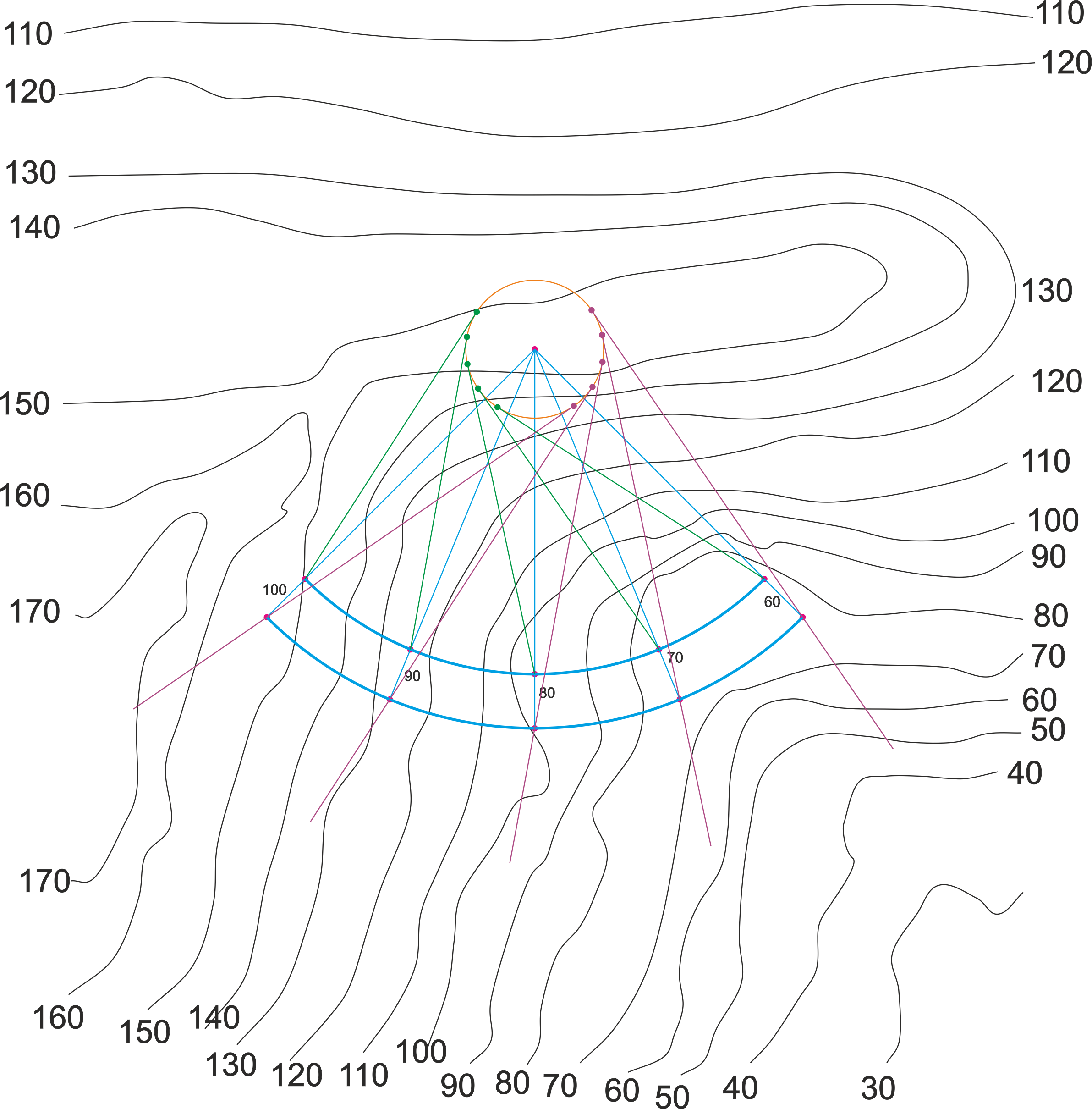
Ahora trazamos las líneas de nivel, usando como centros de arcos los puntos intermedios de los puntos de tangencia en la arista de retroceso y teniendo en cuenta que el intervalo es 1m y la equidistancia 10m.
Si empezamos por el contorno inferior, por la parte de la izquierda, en el primer tramo podemos ver que discurren las líneas de nivel del terreno de cota entre 130 y 170, así que solo dibujaremos esas líneas de nivel en el talud.
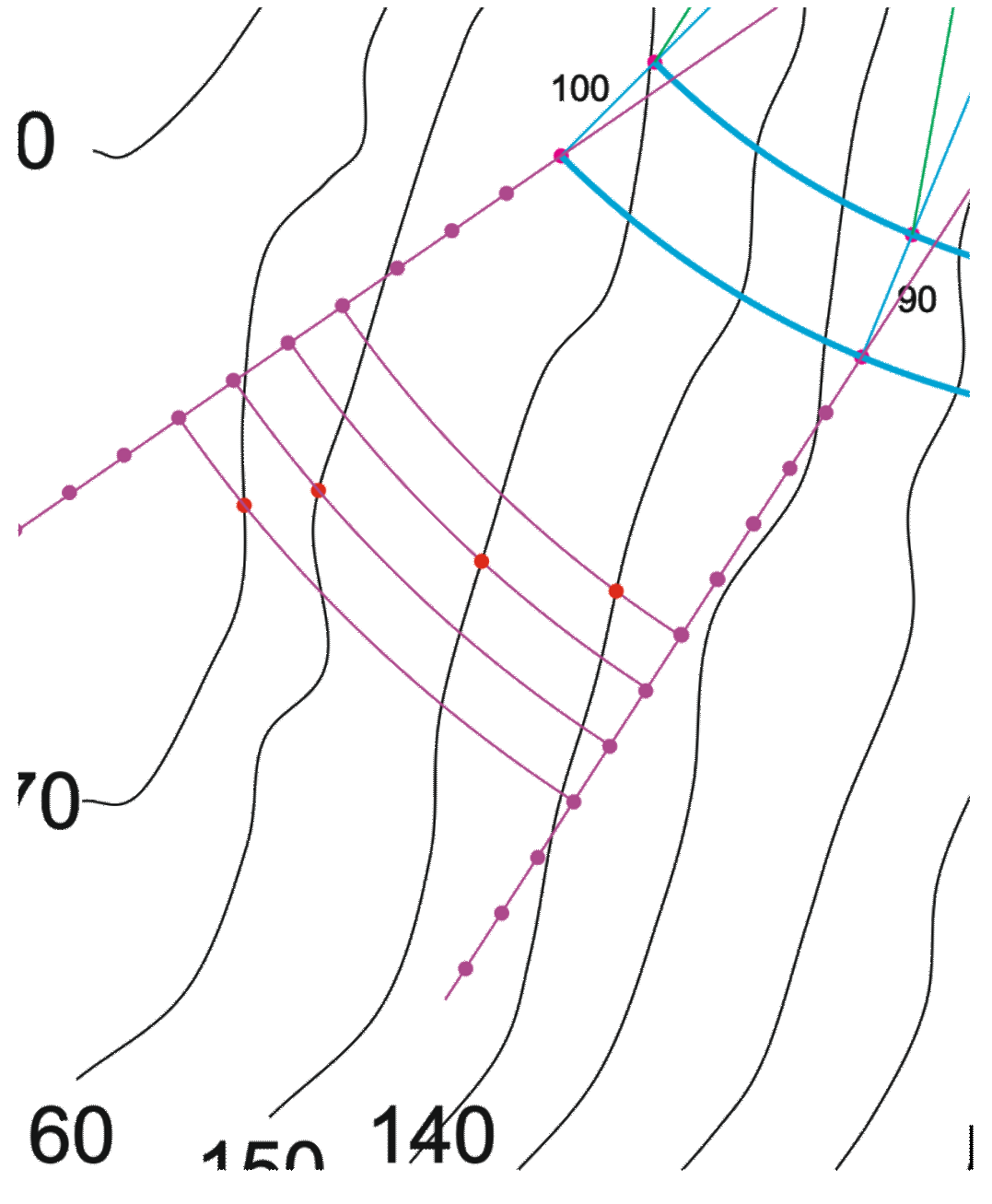
En el último tramo, con las líneas de nivel dadas no tenemos ningún punto común, así que hemos trazado una nueva línea de pendiente desde la arista de retroceso, y la hemos abatido, abatiendo además la sección de la línea de nivel del terreno. Hemos repetido la operación en el extremo derecho de la curva, pero solo a título ilustrativo.
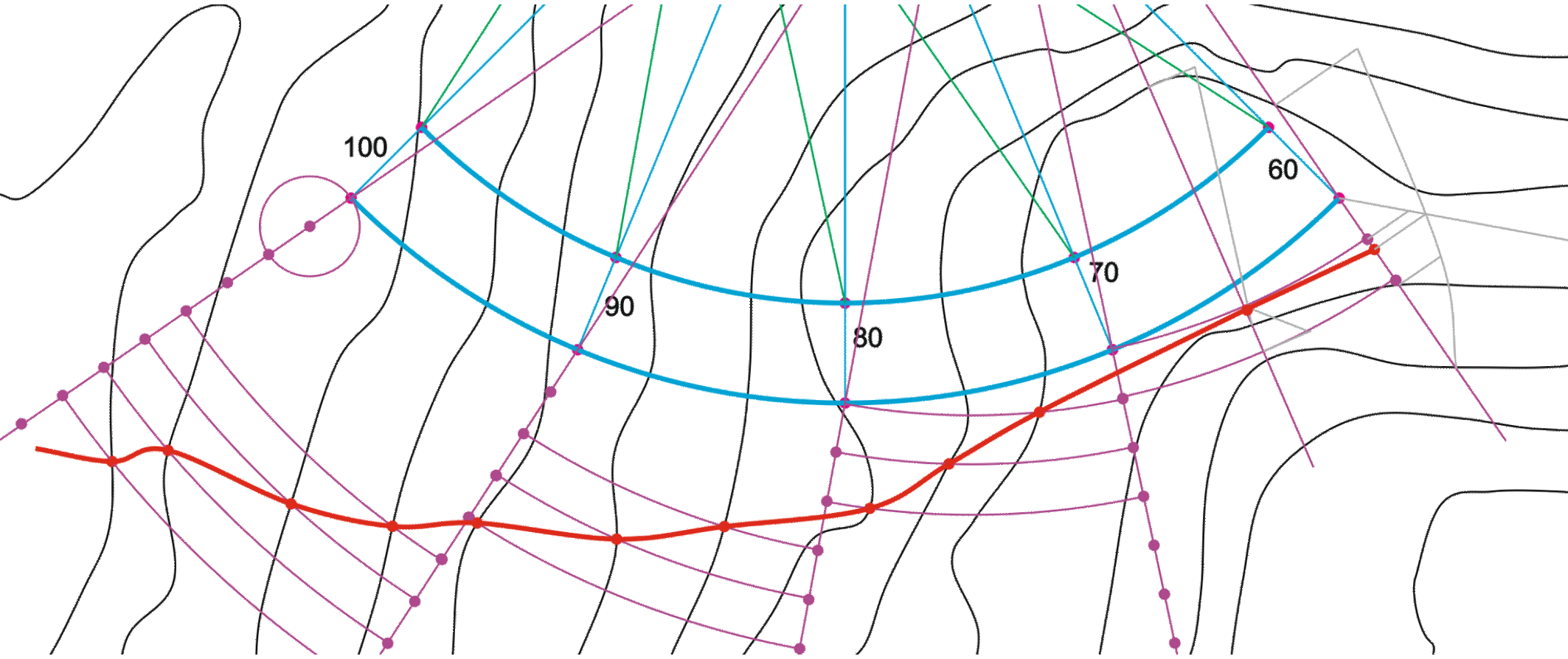
El otro lado también se ha resuelto con normalidad. Aquí está el ejercicio completo: