Introducción

Los primeros trazados de carreteras y vías férreas encadenaban tramos rectos con tramos trazados con arcos de circunferencia. A velocidades relativamente bajas, estos trazados pueden ser correctos, pero a velocidades altas, los vehículos sufren una sacudida peligrosa en la transición de curva a recta o de recta a curva.

La causa es una variación instantánea de la fuerza centrífuga (que depende del cuadrado de la velocidad lineal y es inversamente proporcional al radio de curvatura), ya que se pasa sin transición de un radio de curvatura infinito (recta) a un radio limitado (curva) o viceversa. Naturalmente, cuanto más cerrada sea la curva, mayor es la transición de la fuerza centrífuga.

Para evitar este grave problema, en los trazados de viales en los que se prevé que la velocidad será alta y los radios son relativamente bajos (menores de 2500 m), se añade una curva de transición entre el tramo recto y el tramo curvo, de forma que esta fuerza centrífuga varíe de manera suave desde la salida de un tramo hasta la entrada en el otro.

También se tiene en cuenta que en los tramos curvos se debe realizar una inclinación del firme (peralte) que compense también esta fuerza centrífuga una vez en la curva.

También deben realizarse transiciones en los trazados verticales. Así, para enlazar un tramo ascendente o descendente con uno horizontal o en general con uno con pendiente diferente, debe diseñarse una transición, con el fin de evitar aceleraciones verticales bruscas.

Transiciones entre tramos horizontales

Para enlazar dos tramos rectos, puede usarse:

• Una transición simple mediante un arco de circunferencia
• Una transición mediante un arco y dos curvas de transición intermedias (clotoides)
• Una transición mediante dos clotoides (clotoide de vértice)

Suele ser frecuente en la práctica la utilización de los grados centesimales (gonios), para el tratamiento de los ángulos. La equivalencia entre radianes, grados sexagesimales y gonios se muestra en la siguiente tabla:

Transición simple entre dos tramos rectos mediante un arco

La curva transición es un arco tangente a los dos tramos rectos, y su radio viene dado en función de los parámetros de la vía (a mayor velocidad, mayor radio). El centro del arco se encuentra en la bisectriz del ángulo formado por las dos rectas.

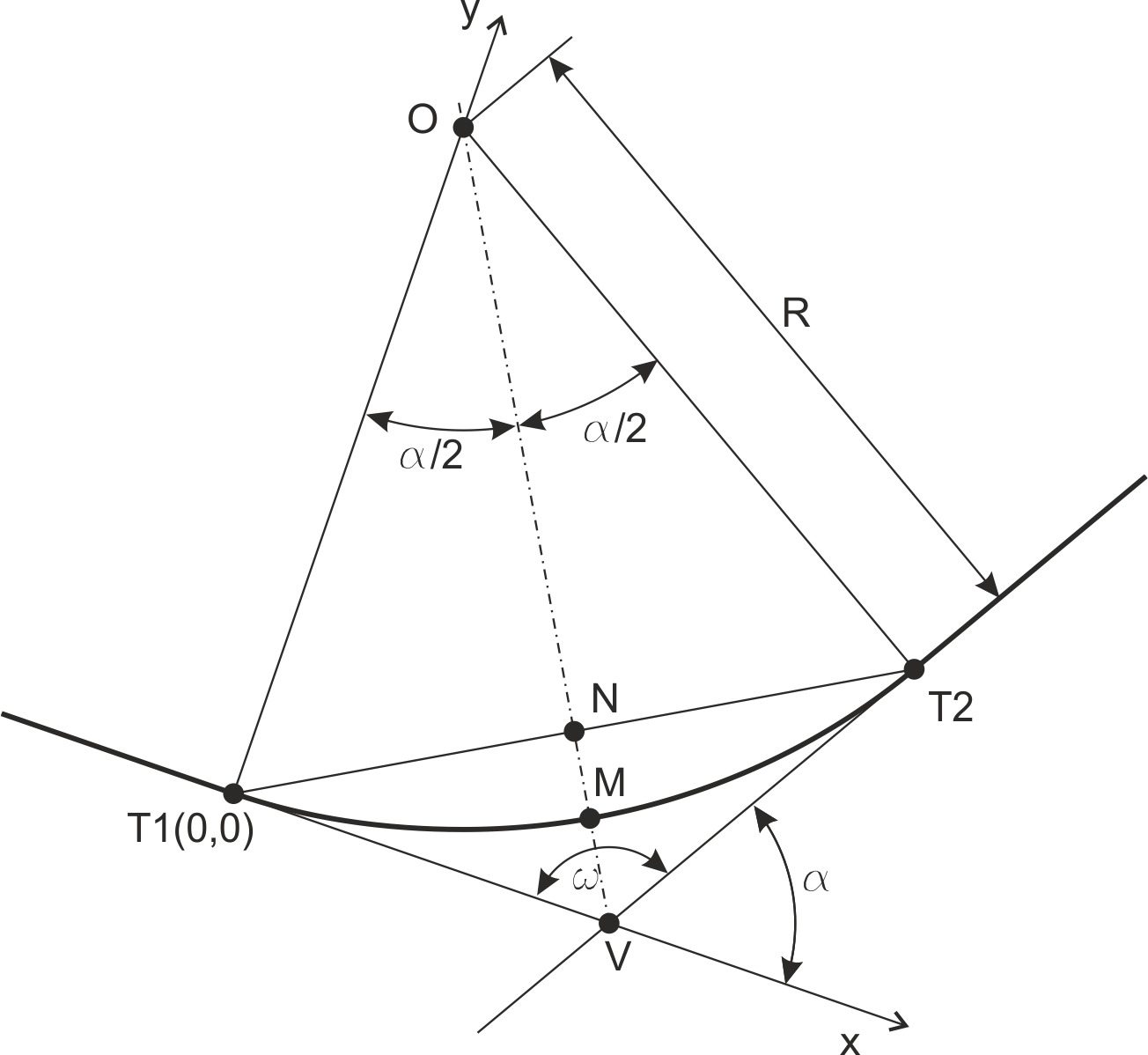
En la figura, los distintos elementos y parámetros son:

• R: Radio de la curva
• O: Centro de la curva
• Segmentos T1-V y T2-V: Semitangentes (miden lo mismo) – TH
• Arco T1-T2: Segmento de enlace (arco) – Longitud LC
• Segmento T1-T2: Cuerda larga – CL
• α: ángulo de la curva, también llamado ángulo en el centro
• ω: ángulo en el vértice de alineaciones (α y ω son complementarios)
• Segmento V-M: Bisectriz externa
• Segmento O-M: Bisectriz interna
• Segmento M-N: Ordenada media – m

Podemos ver que, a efectos de posible cálculo numérico y/o de coordenadas, hemos supuesto el origen de coordenadas en el punto de inicio del tramo de transición T1, considerando el eje X en la dirección de entrada.

Las relaciones entre esos elementos son:

Clotoide

Existe una curva en la cual el radio de curvatura varía de forma continua, denominada clotoide (también denominada radioide de arcos o espiral de Cornú).

Esta curva se adapta perfectamente a las necesidades de estos tramos de transición en el trazado de viales, ya que permitirá una transición suave de la fuerza centrífuga entre los puntos inicial y final del recorrido.

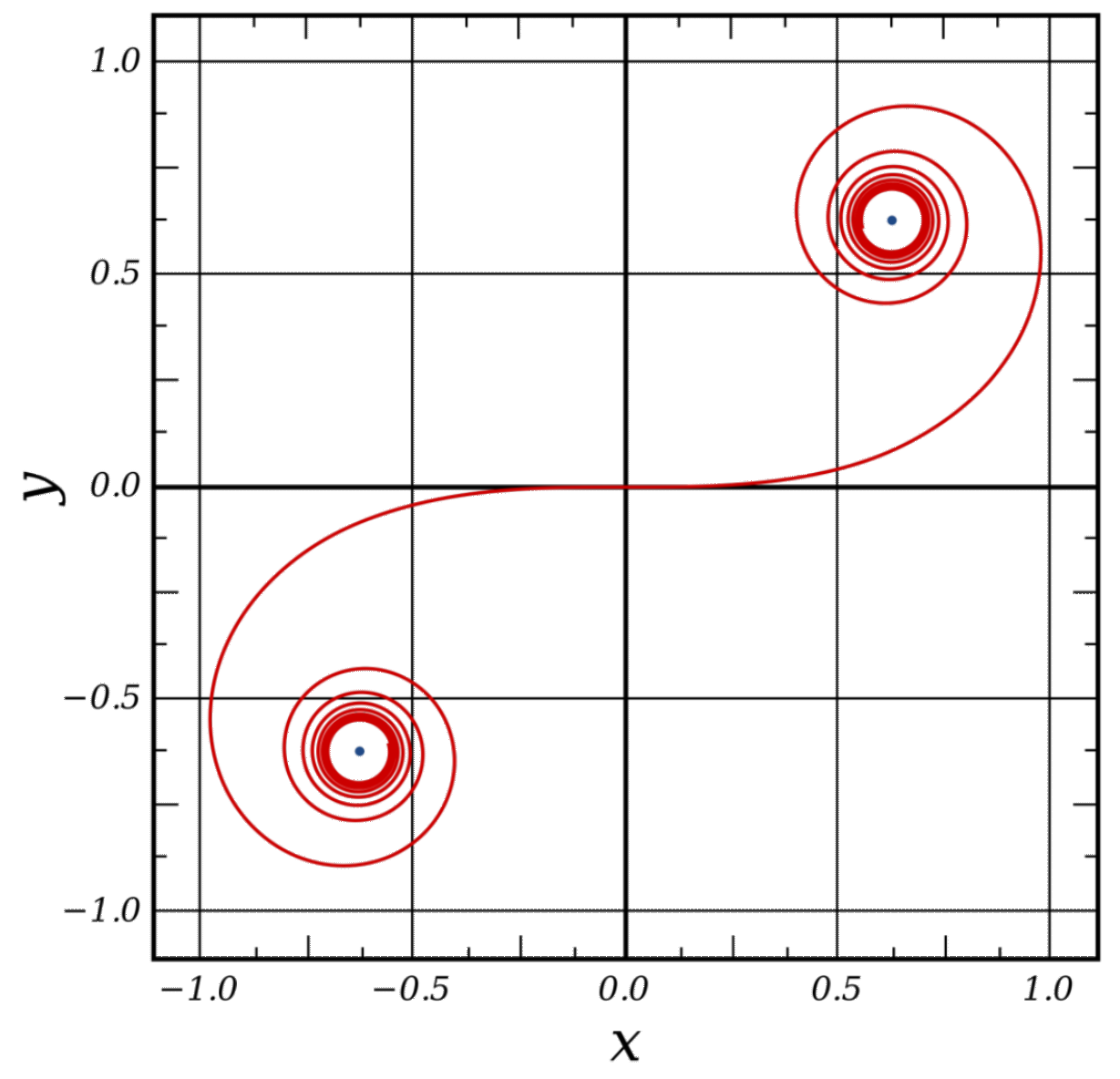
La ecuación de la clotoide es:

p * s = A²

donde p es el radio de curvatura en uno de sus puntos (para el punto inicial, el radio es infinito), s es el desarrollo o longitud desde el punto de origen a ese punto, y A es la constante (parámetro) de la curva.

La principal propiedad de la clotoide es que la curvatura en cualquiera de sus puntos es proporcional a la distancia recorrida desde el origen. Así, en un enlace entre recta y curva, partiendo de una velocidad angular nula llegamos a la velocidad angular de la curva mediante una aceleración angular constante.

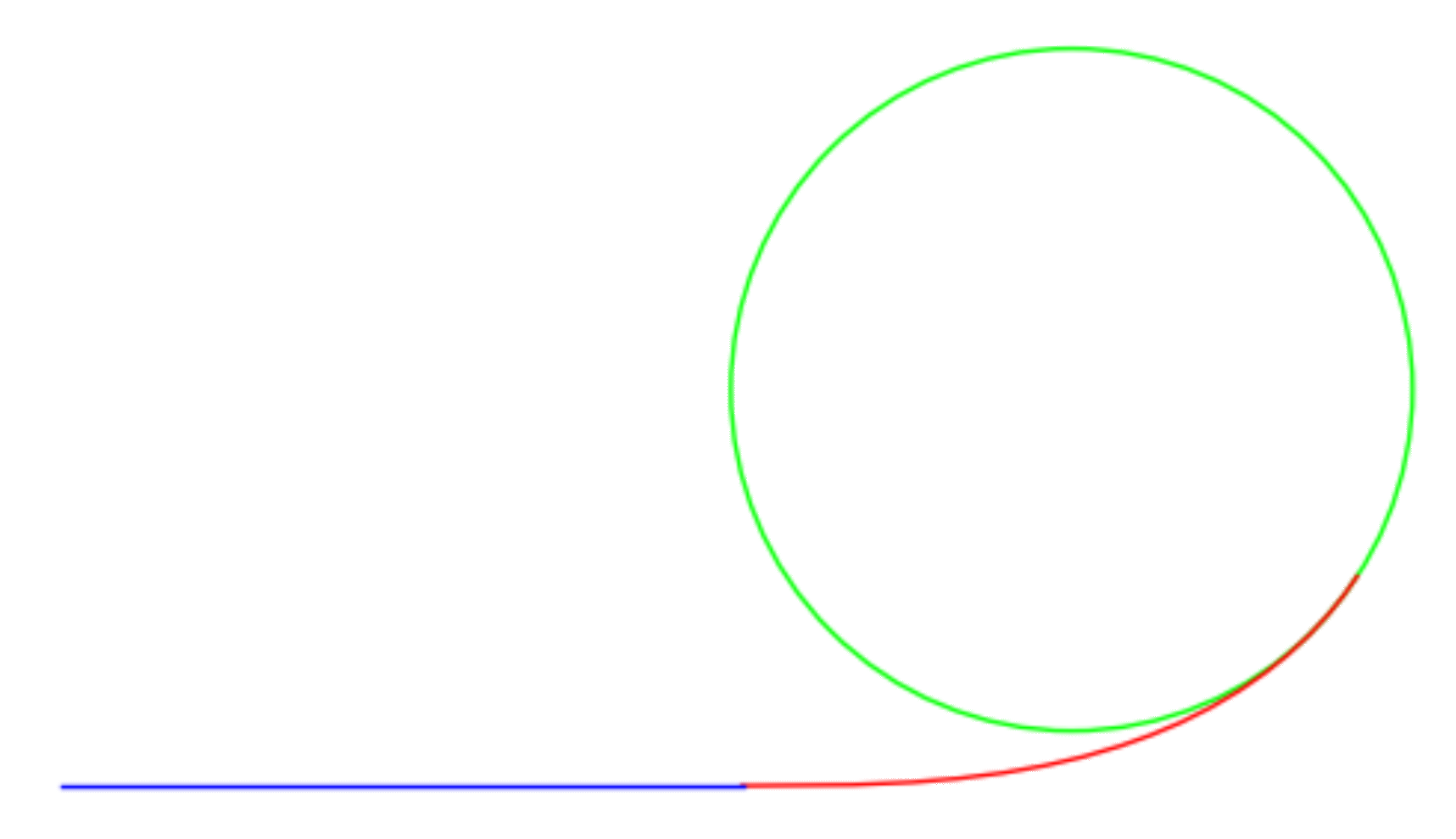
Transición entre dos rectas mediante arco y dos clotoides intermedias

En la figura siguiente, la unión entre dos tramos rectos, originalmente enlazados mediante un arco de centro O y radio R, va a completarse con dos clotoides de enlace entre los tramos rectos y un arco central.

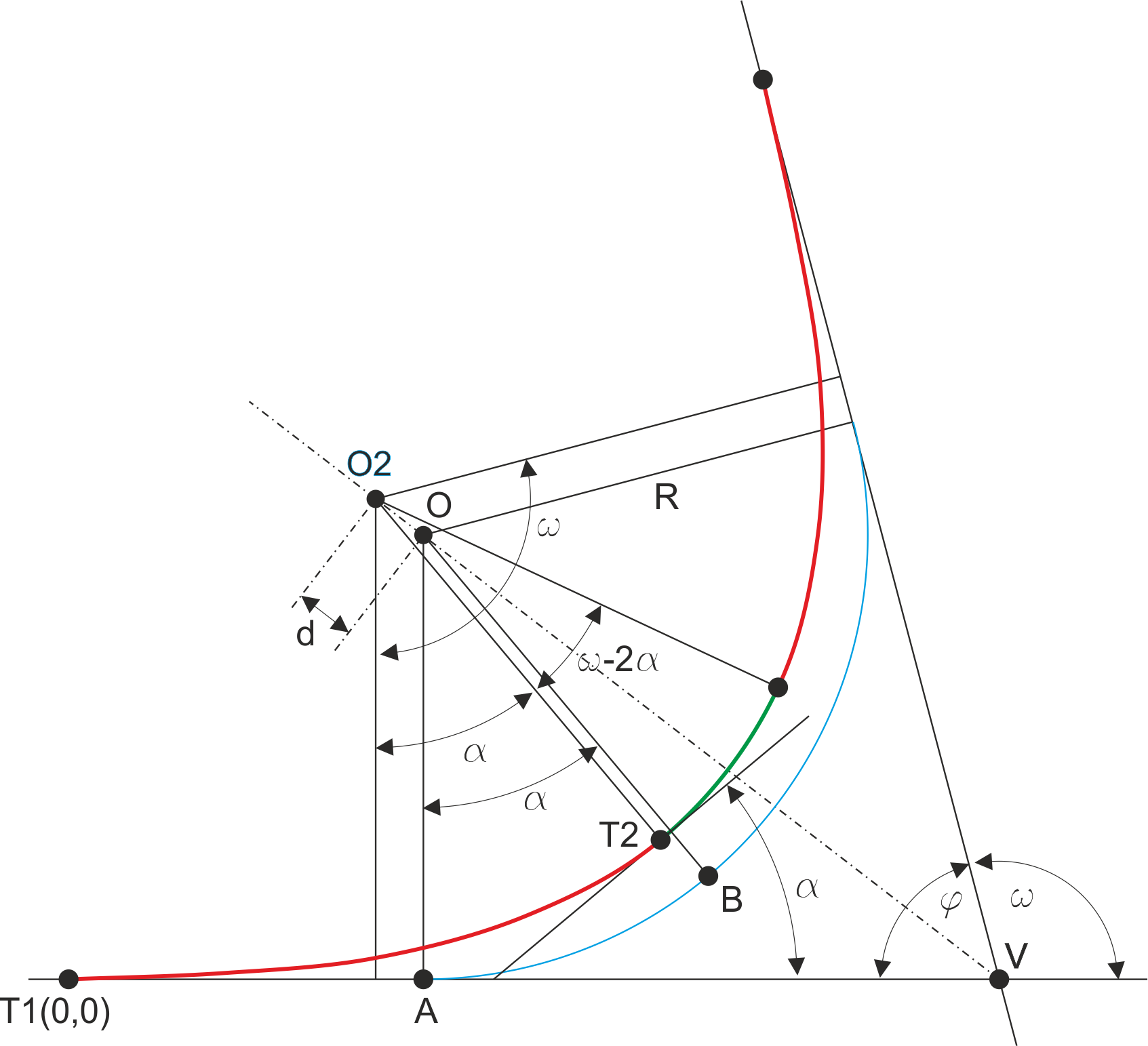
En lo que respecta a la clotoide (trazada en rojo), se considera el origen de coordenadas e inicio del trazado al punto T1, y el final del trazado al punto T2, que es donde va a comenzar el arco (en verde, en la figura). La segunda clotoide es simétrica de la primera con respecto a la bisectriz del ángulo que forman los dos tramos rectos. Por lo tanto, el radio inicial de la clotoide es infinito (en T1), y el radio final es R (en T2).

Si uno de los parámetros de diseño es el radio R del arco de enlace, en la figura puede verse que el tramo de arco final (en verde) sufre un desplazamiento con respecto al arco original (en azul), siendo el nuevo centro el punto O2. Esto se traduce en un retranqueo del radio (d). Este retranqueo, en el eje Y, también es denominado ΔR0.

El ángulo φ es el ángulo en el vértice de las alineaciones rectas, y ω es el ángulo central, el que forman las perpendiculares por el centro de curvatura hasta los trazados rectos (φ y ω son suplementarios).

El ángulo de desviación α es el que determina la tangente a la clotoide en su punto final T2, punto donde también es tangente al tramo de arco.

Para el trazado, partimos de un supuesto en el que, dados los trazados rectos a unir, conocemos el radio de enlace R, y el parámetro A que define la clotoide.

Llamamos L a la longitud de la clotoide, o sea, la longitud de la curva T1-T2.

Llamamos L_C a la longitud del arco de circunferencia final o arco residual (tramo verde). La longitud LC es

L_C = R * (ω – 2 α)

Como buena solución, se puede tomar que la longitud de la rama de clotoide L sea al menos el doble de la longitud del arco original abarcado por el mismo ángulo a, esto es, el arco AB (aunque también es posible que nos definan una longitud del arco residual diferente).

Así que en este caso si AB = α * R, entonces L = 2 AB = 2 * α * R.

Como sabemos por la ecuación de la clotoide, en el punto T2:

p * s = A²

O lo que es lo mismo

R * L = A²

De donde podemos obtener L.

Podemos encontrarnos con tres casos:

• Si ω > 2α, o lo que es lo mismo, EXISTE una parte del arco original, se trata de una clotoide normal. En este caso el problema debería proporcionar el radio R de enlace original y el parámetro A de la clotoide.
• Si ω = 2α, la curva original (arco residual) desaparece y solo quedan los dos tramos de clotoide. Se trata de una clotoide de vértice.
• S ω < 2α, se daría un caso imposible, ya que el arco sería negativo y las clotoides se solaparían. Estos casos se corrigen variando el parámetro A de la clotoide.

A efectos de cálculo, llamaremos α_L al ángulo que forma la tangente a la clotoide en cualquier punto de su recorrido. Su valor irá variando desde 0 (en el punto T1) hasta a (en el punto T2). Su valor es, según el criterio de que la longitud de la clotoide es el doble del arco original:

α_L = L / 2 R

O lo que es lo mismo

α_L = L / 2 (A²* L) = (L/A)²/2

Para representar la curva, podemos calcular las coordenadas de puntos intermedios entre T1 y T2, tomando longitudes intermedias entre 0 y L.

Sin entrar en detalle matemático, estas coordenadas las calculamos por unas integrales de Fresnel y el desarrollo en serie de funciones circulares:

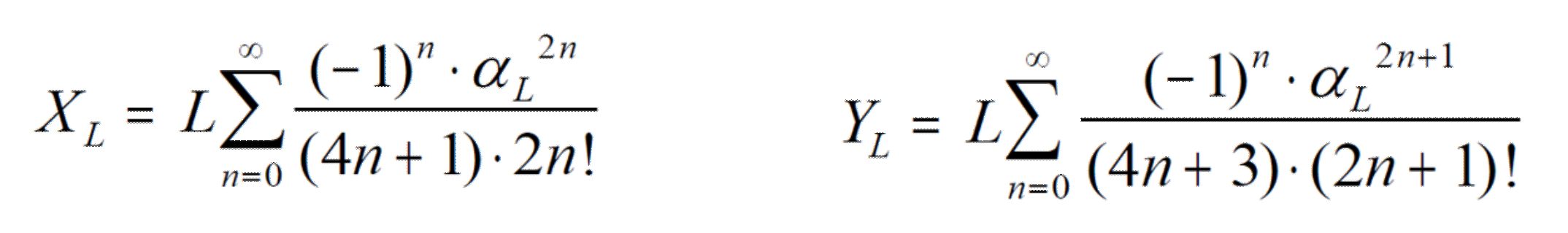
Desarrollando los primeros términos:

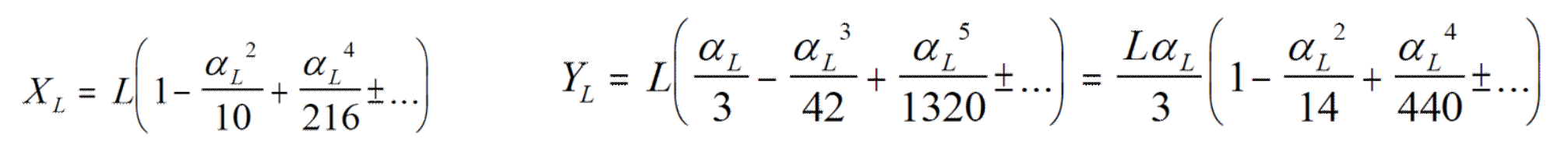
O lo que es lo mismo, sustituyendo α_L en las ecuaciones:

En la práctica podemos hacer un buen cálculo tomando únicamente el primer término.

Una vez calculados los puntos de la clotoide, podemos calcular el retranqueo del radio en el eje Y:

∆R0 = Y₀ – R₀ (1 – cos⁡(α_L0))

Y la distancia d entre O y O2

d= ∆R0 / cos⁡(ω/2)

En una hoja de cálculo (descargable más abajo) se muestra un ejemplo del cálculo de una clotoide, siendo el archivo una plantilla válida, con mínimas modificaciones, para calcular cualquier clotoide.

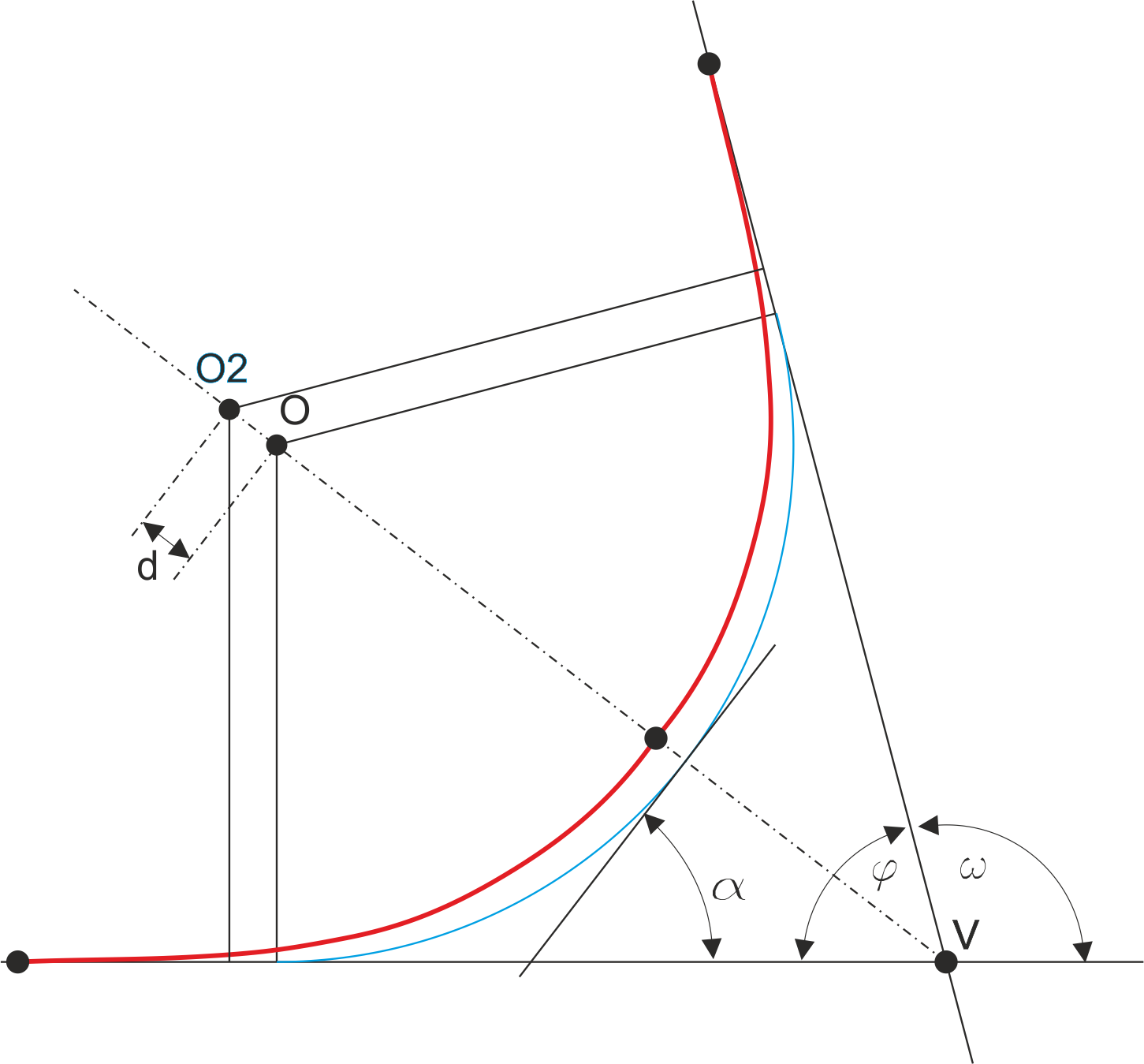
Transición entre dos rectas mediante dos clotoides

La clotoide puede enlazar tramos rectos con tramos circulares, pero también puede enlazar dos tramos rectos mediante dos tramos simétricos de clotoide (clotoide de vértice), o dos tramos circulares de diferente radio.

Se calcula de forma idéntica a la anterior, salvo que se fuerza el problema (ajustando el parámetro A de la curva) a que el arco residual sea nulo.

Otras consideraciones

Para el diseño de la clotoide se tendrán en cuenta varios factores además del radio de las curvas implicadas.

Estos factores pueden ser el peralte diseñado, que también puede compensar la fuerza centrífuga, la visibilidad (el conductor debe percibir con suficiente antelación la proximidad de la curva, para lo cual se tendrán en cuenta las pendientes permitidas), las velocidades nominales de los tramos, las longitudes máximas de tramos curvos y rectos (la legislación actual limita las longitudes máximas de tramos rectos y curvos de los trazados), etc…

Acuerdos verticales

Para suavizar los cambios de pendiente que se producen cuando un tramo horizontal pasa a un tramo con pendiente, o viceversa, de forma que los vehículos no sufran una aceleración vertical brusca, y también para facilitar la visibilidad en puntos más allá de los cambios de rasante, se utilizan curvas de acuerdo vertical basadas en parábolas.

Estas parábolas vienen definidas por el parámetro K_V, que es el radio de la circunferencia osculatriz en el vértice de las mismas. La ecuación de la curva es esta:

y = x² / (2 * K_V)

Fijado el origen en el punto de tangencia con la alineación inicial, cada valor de y se obtiene para el x, siendo ésta el segmento vertical de distancia entre la alineación recta y el correspondiente de la curva.

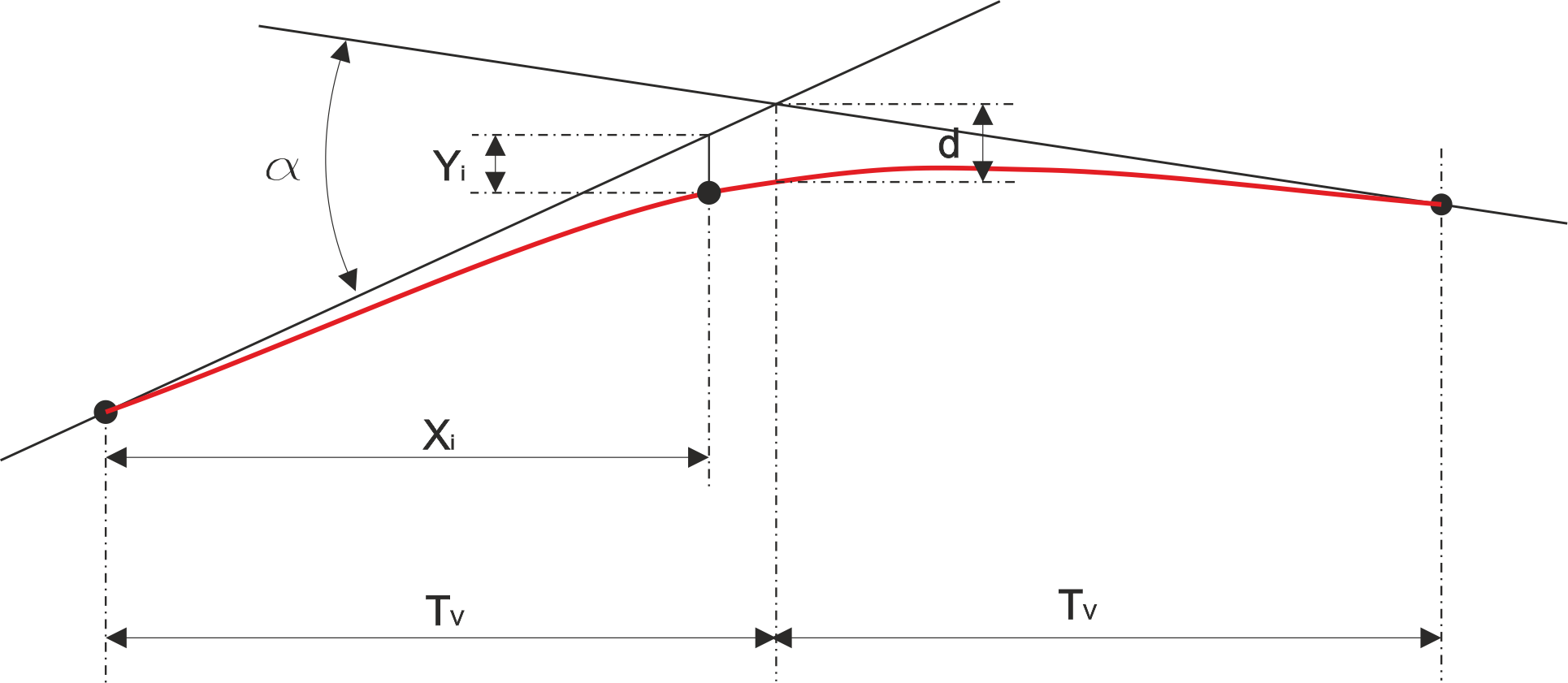
En la figura, α es el ángulo entre las alineaciones originales (diferencia algebraica de alineaciones en tanto por uno).

T_V es la longitud horizontal de cada tramo de tangente hasta la intersección de alineaciones.

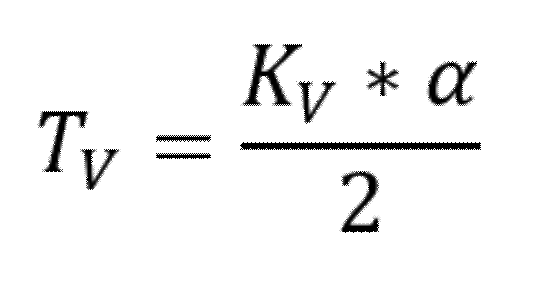
d es la longitud vertical entre el vértice de alineaciones y la curva, o sea, el valor de y cuando x = T_V

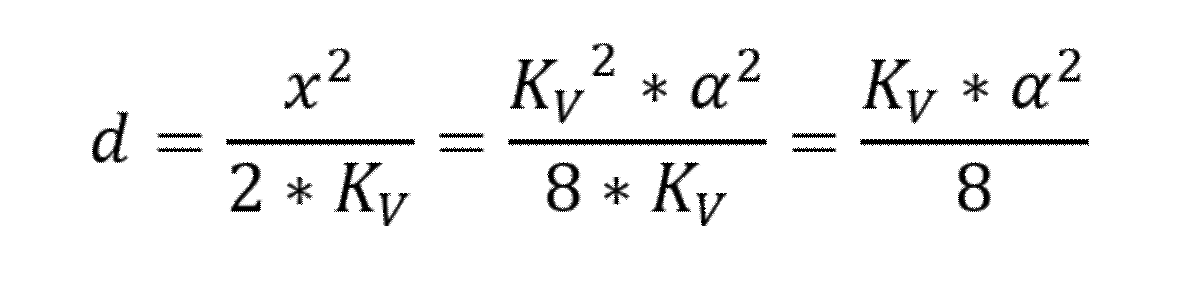
ANEXO: PLANTILLA EXCEL PARA EL CÁLCULO DE CLOTOIDES (PULSAR PARA DESCARGAR)