Conceptos

En las obras, cuando dos planos convergen, en lugar de determinar la intersección mediante una arista viva (la intersección de dos planos es una recta), se suele utilizar una superficie de transición o acuerdo.

Esas superficies, que se diseñan para evitar cambios bruscos, deben ser tangentes a ambos planos, por lo que son superficies regladas desarrollables: conos y cilindros.

Acuerdos cónicos

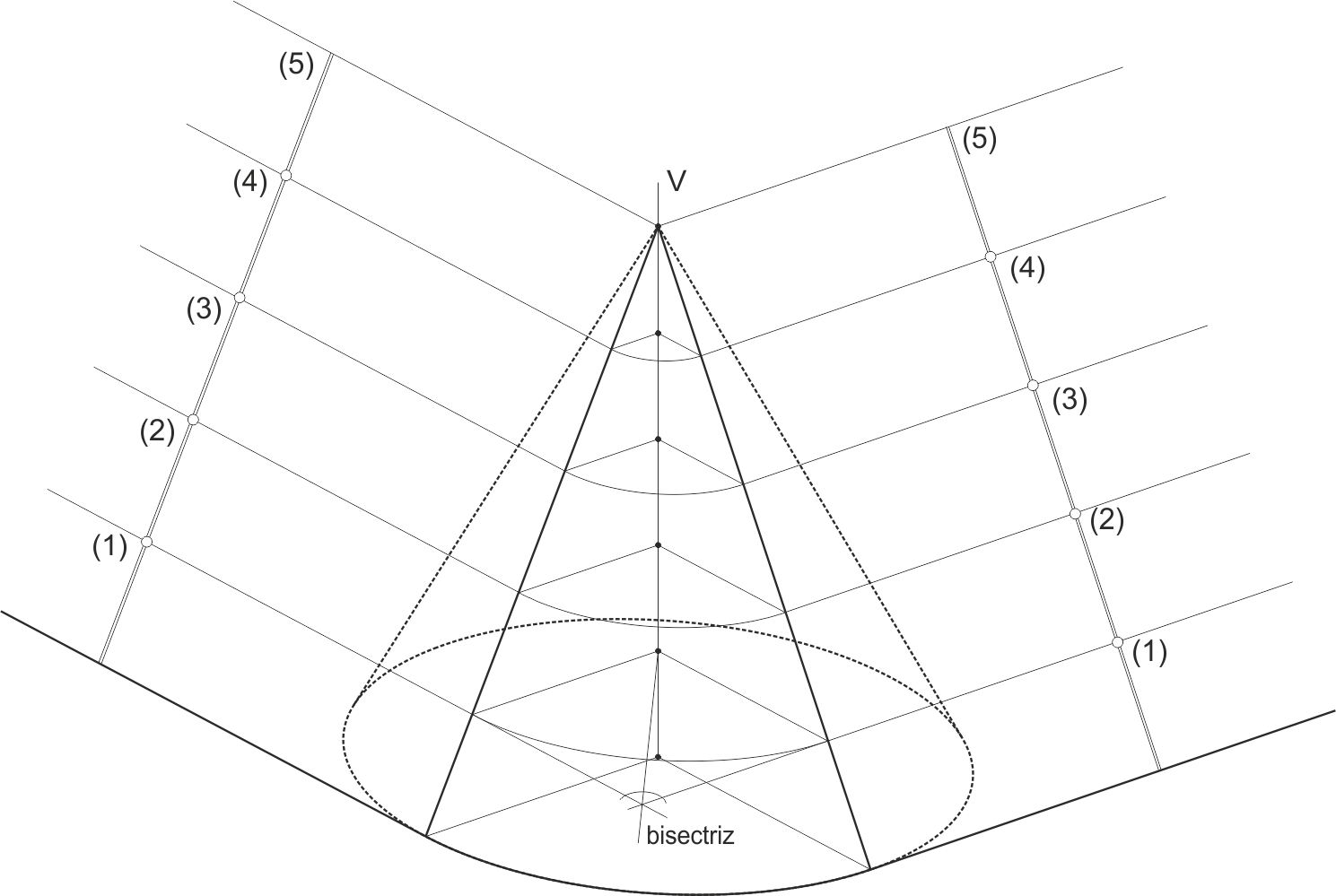
Si la transición entre dos planos se realiza mediante un cono (o un tronco de cono), necesariamente el vértice del mismo se encuentra en la recta intersección de ambos planos (y, por tanto, es la intersección de las horizontales del plano de cota igual a la de dicho vértice).

Las horizontales de igual cota en ambos planos serán tangentes a las circunferencias directrices horizontales del cono de la misma cota (estas circunferencias son las líneas de nivel del cono). Y los centros de estas circunferencias (incluido el centro de la base) además se encontrarán en las bisectrices de las líneas de nivel (horizontales) de los planos.

En estos ejemplos se muestra la intersección de dos planos del mismo talud (pendiente), mediante un cono que, por esta misma circunstancia, será recto. Uno de los parámetros que deben definirse es el radio de una de las directrices circulares del cono, o bien la cota del vértice del cono. En este caso, se ha fijado el vértice en la cota 5.

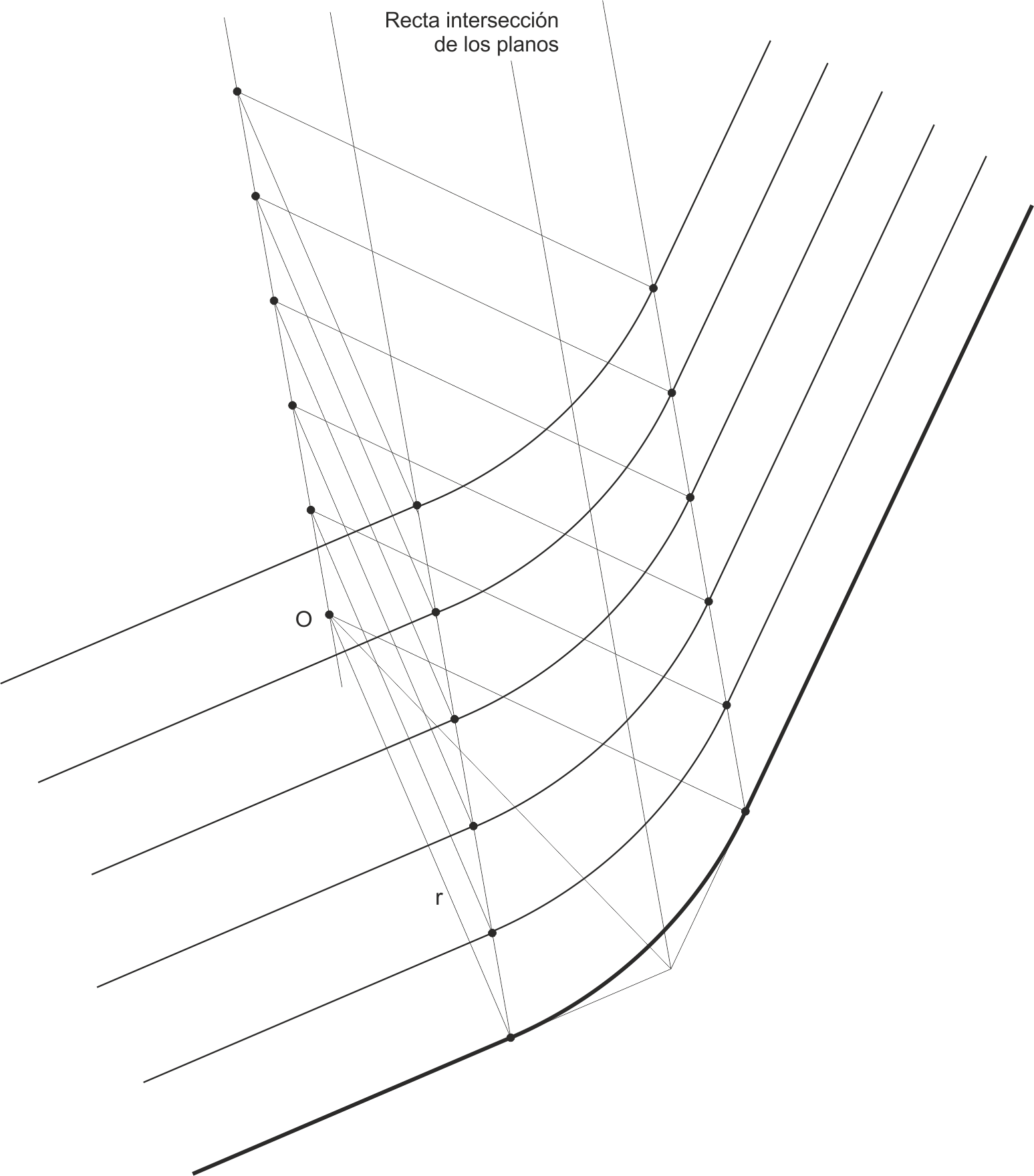
Cuando los planos que van a enlazarse no tienen el mismo talud, el cono de enlace no es recto, ya que las circunferencias directrices, tangentes a las líneas de nivel de los planos, no van a tener su centro en la misma proyección. Las proyecciones de estos centros, sin embargo, estarán todos alineados con la proyección del vértice del cono. También podremos comprobar que para todas las líneas de nivel los puntos de tangencia están alineados, formando las líneas de tangencia del cono con los planos. Así, el cono es de eje oblicuo (no es de revolución), aunque sus secciones horizontales sean circunferencias.

En el siguiente ejemplo, se ha fijado como dato del problema la cota del vértice V del cono (5) y el radio del enlace en la cota (2), de valor r. Empezamos dibujando la circunferencia de enlace en la cota 2 (de radio r conocido), de centro O(2), que nos da los puntos de tangencia S y T en las horizontales de los planos de esta cota. Uniendo S y T con V obtenemos las líneas de tangencia, que contendrán todos los puntos de tangencia mencionados. A partir de esos puntos de tangencia podemos obtener los centros de todas las circunferencias de enlace, que estarán alineados con O y V.

Acuerdos cilíndricos

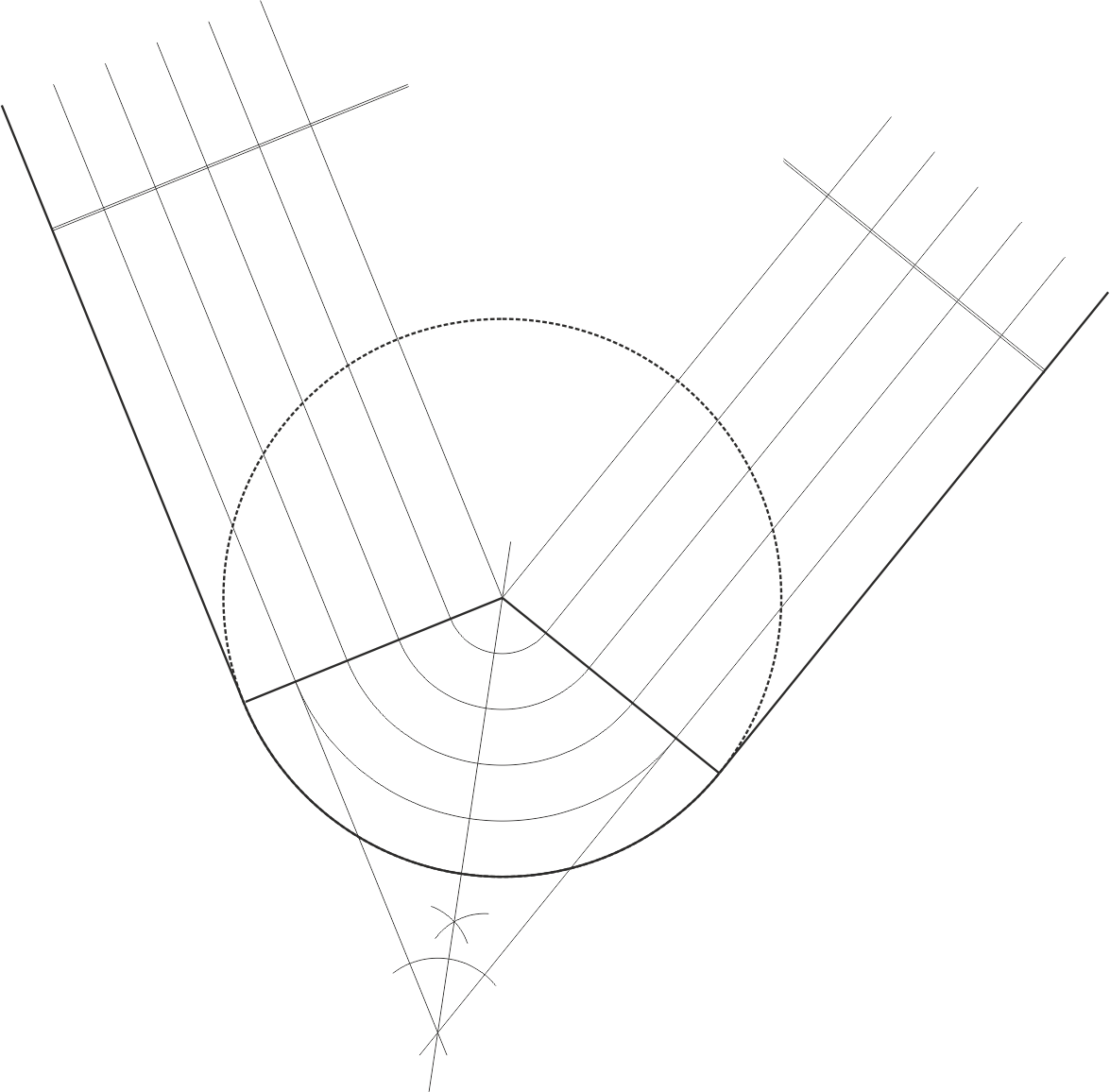
El acuerdo cilíndrico es una variante del acuerdo cónico en la cual el vértice del cono es impropio, con lo cual los radios de todas las circunferencias de enlace son iguales. Las rectas que unen los puntos de tangencia y la que une los centros de las circunferencias de enlace son todas paralelas a la recta de intersección de los planos.
El dato de diseño es el radio r de enlace deseado.

Empezamos dibujando la recta intersección de los planos. Con el radio r encontramos el arco de enlace de dos horizontales cualesquiera de igual cota (en el ejemplo por comodidad hemos cogido las trazas), que nos dan los puntos de tangencia S y T. Las paralelas por S y T a la recta intersección de los planos proporcionan todos los puntos de tangencia, a partir de los cuales podemos encontrar los centros de todas las circunferencias de enlace (que siguen también la misma dirección). Todos los arcos de enlace son idénticos.

En el caso del acuerdo cilíndrico, aunque los planos sean del mismo talud, la solución siempre es un cilindro de eje oblicuo.