Introducción

En una sección plana a un cono, si el ángulo β que forman el eje y el plano que corta a la superficie cónica es menor que el semi ángulo cónico α, la curva intersección es una curva abierta de dos ramas, denominada hipérbola.

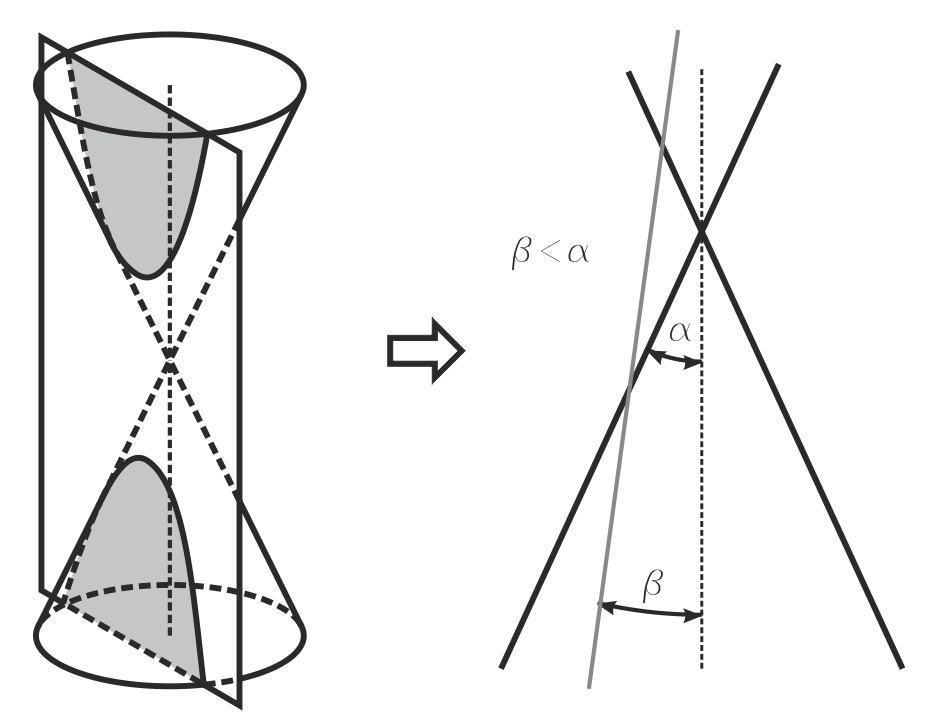
Si el plano secante pasa por el vértice, la curva se degenera en dos rectas, que coinciden con dos generatrices de la superficie cónica, y que se cortan, naturalmente, en el vértice.

Elementos de la Hipérbola

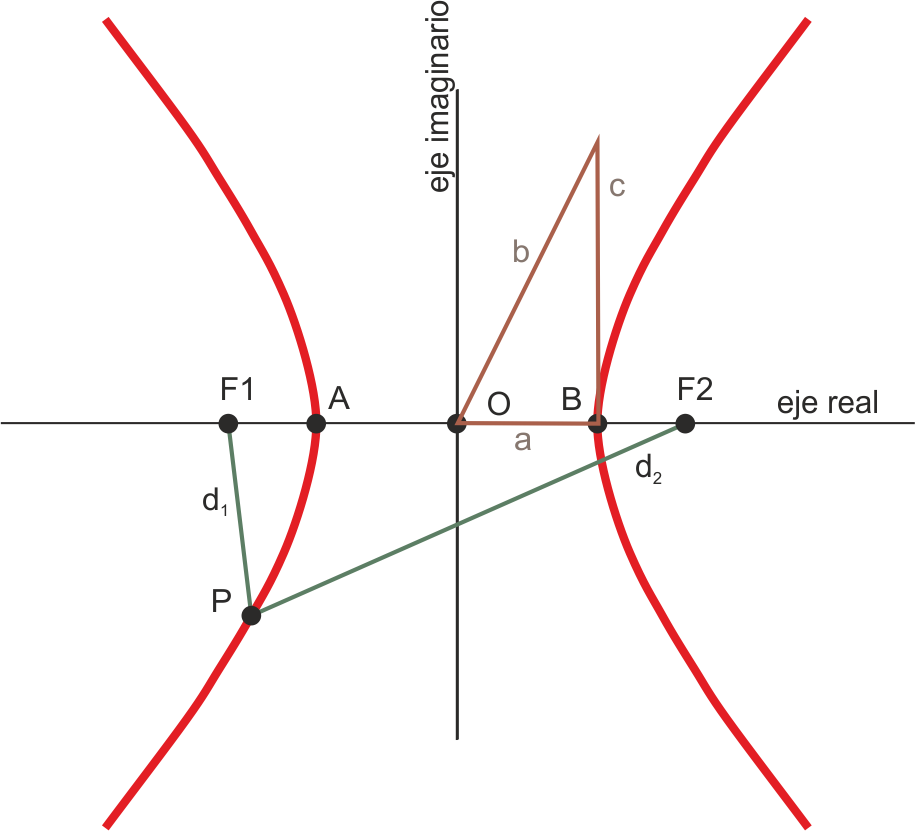
En la figura de arriba, los elementos de la hipérbola son:

• A, B = Vértices
• O = Centro
• F1 y F2 = Focos
• Eje real (pasa por los vértices)
• Eje imaginario (perpendicular al real por el centro O)
• Las distancias notables en la hipérbola son:
• AB = 2a (en el eje real)
• F1-F2 = 2c = Distancia focal
• d1 y d2 = Radiovectores de P (segmentos que lo unen a los focos)

Se cumplen las siguientes propiedades:

• |d1 – d2| = 2a (constante para todos los puntos)
• b2 = a2 + c2 (Pitágoras)

La hipérbola puede considerarse como una elipse cuya parte central es impropia. Veremos que las propiedades de ambas curvas son muy similares.

Excentricidad

En el caso de la hipérbola, la excentricidad equivale al cociente entre el eje mayor (2a) y la distancia focal (2c) y siempre es mayor que la unidad. Cuanto mayor sea la excentricidad, más afinada será la cónica.

La Hipérbola como Lugar Geométrico

Los puntos de la hipérbola tienen una propiedad que permite definirla como el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos (focos) es constante (ver figura inicial de la hipérbola).

Esa constante es igual a 2a, la distancia entre los dos vértices de la hipérbola.

La hipérbola también puede definirse como el lugar geométrico de los centros de las circunferencias tangentes a otra dada que pasan por un punto fijo exterior a ésta (figura de la derecha). Y también es el lugar geométrico de los puntos que equidistan de una circunferencia y de un punto exterior a ésta (esta propiedad es derivada de la anterior).

Ecuación matemática de la Hipérbola

Considerando el centro de la hipérbola como el origen de coordenadas (0,0), y siendo las coordenadas de un punto P(X,Y), según la figura de la página anterior, se cumple:

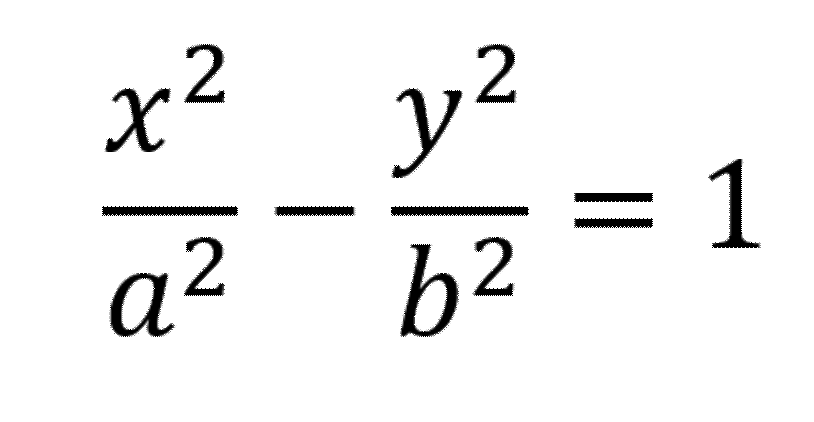
Más elementos de la Hipérbola

Las circunferencias focales de la hipérbola tienen como centro los focos y como radio 2a (en la figura, AB=|d1-d2|=2a).

La circunferencia principal de la hipérbola tiene como centro el de la curva y como diámetro 2a.

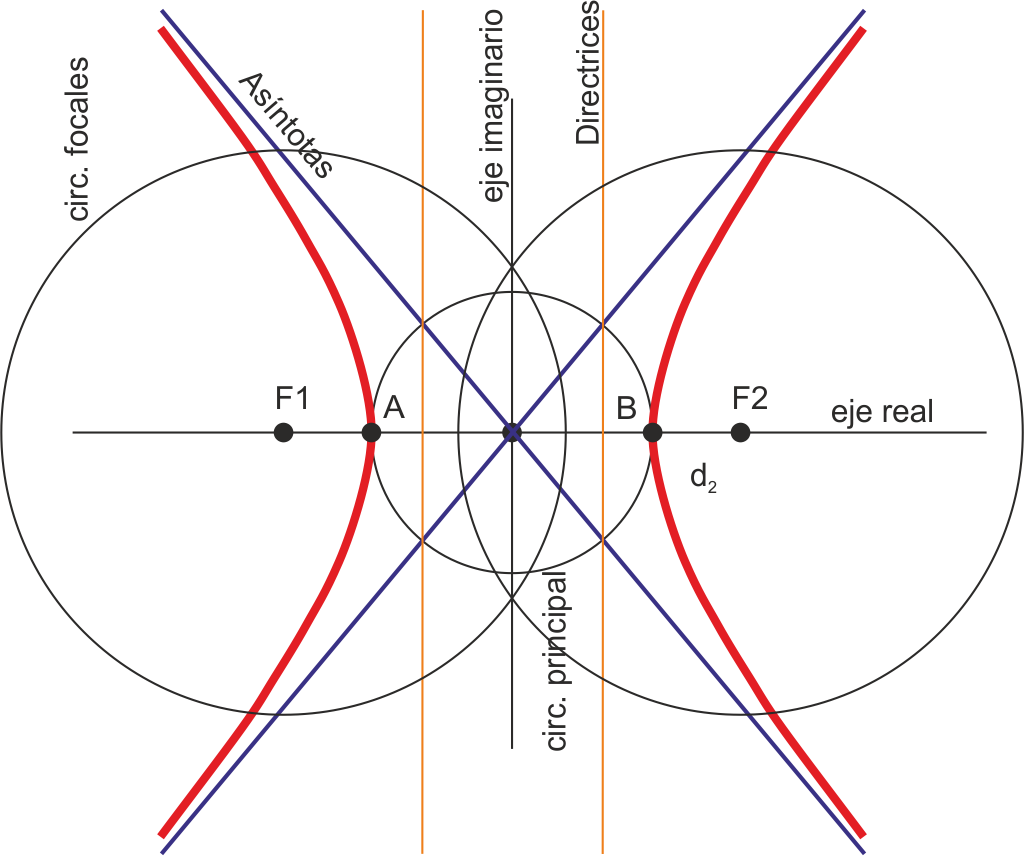
Asíntotas

Las asíntotas de la hipérbola son las tangentes a la curva en el infinito. Los ejes son bisectrices de las asíntotas.
Las asíntotas pueden trazarse con ayuda de la circunferencia principal y la de diámetro OF (O es el centro de la cónica).

Dos hipérbolas son conjugadas cuando comparten las asíntotas, pero sus ejes están intercambiados.
Una hipérbola es equilátera si sus asíntotas forman 45º grados con los ejes.

Directrices

Las directrices de la hipérbola son las rectas polares de los focos respecto de la curva, y pueden obtenerse a partir de la circunferencia principal y de las asíntotas.

Diámetros en la Hipérbola

Se denomina diámetro real de la hipérbola a cualquier recta que pase por el centro y corte a la curva. Se denomina diámetro imaginario a cualquier recta que pase por el centro y no toque a la curva. El sector correspondiente a los diámetros imaginarios está determinado por las asíntotas.

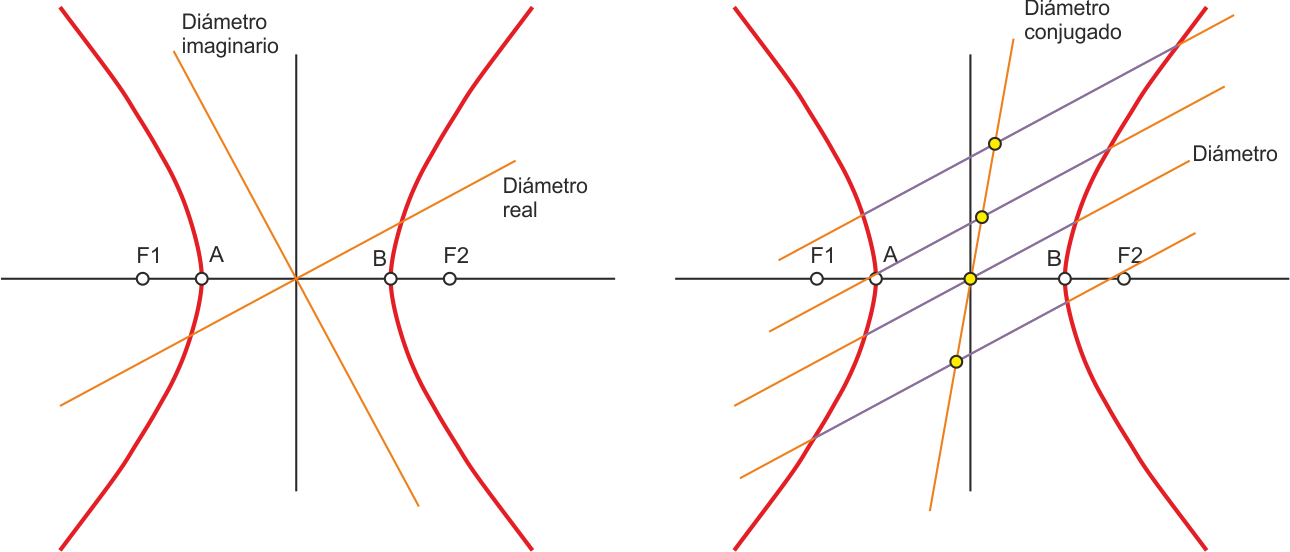
El diámetro conjugado de uno dado es el lugar geométrico de los puntos medios de las cuerdas paralelas a él. Si un diámetro es real, su conjugado es imaginario, y viceversa.

Las tangentes a la hipérbola en los extremos de un diámetro real son paralelas al diámetro conjugado imaginario.

Propiedades especiales de la Hipérbola

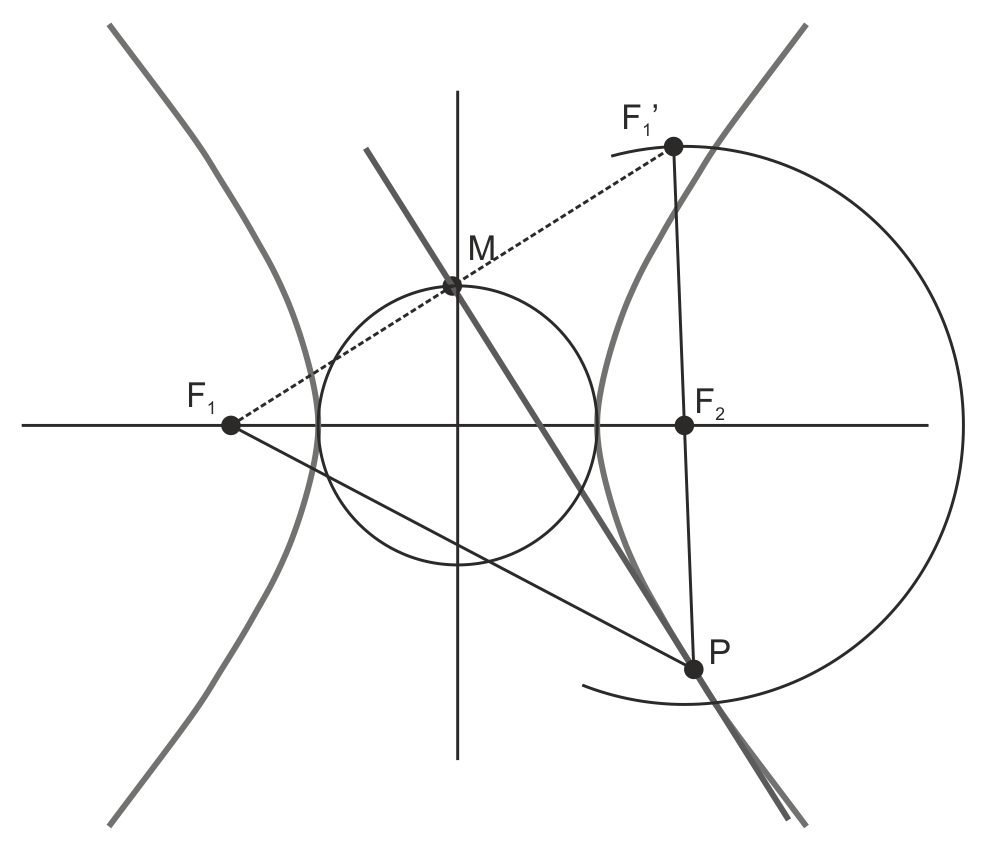
La circunferencia focal de un foco es el lugar geométrico de los puntos simétricos del otro foco con respecto a cualquier tangente a la hipérbola.

La circunferencia principal es el lugar geométrico de los puntos (M) que, estando en las tangentes, son los intermedios entre un foco y su simétrico con respecto a cualquier tangente a la hipérbola, o sea, de los pies de las perpendiculares a las tangentes desde los focos.

El punto P, punto de contacto de una tangente con una hipérbola, está alineado con un foco y el simétrico del otro con respecto a esa tangente. La tangente es bisectriz del ángulo formado por P, F1 y F1’.

Teorema de Dandelin en la Hipérbola

Dada una superficie cónica y un plano que la secciona formando una cónica, siempre se pueden dibujar una o dos esferas (una en el caso de la parábola) tangentes interiores a la superficie cónica y a su vez tangentes al plano de corte.

El Teorema de Dandelin para la hipérbola enuncia que los puntos de tangencia F1 y F2 de las esferas con el plano de corte son los focos de la hipérbola, y los planos que contienen a las circunferencias de contacto de las esferas con la superficie cónica intersecan al plano de corte en dos rectas que son las directrices de la cónica.

En la figura de abajo se representa la interpretación plana del Teorema de Dandelin en la Hipérbola, mediante una vista en la que el plano de corte queda perpendicular al papel, y se representa por una recta. El plano secante corta a las generatrices aparentes (las más exteriores) en los puntos A y B, que serán los vértices de la hipérbola.

En esta interpretación las esferas tangentes aparecen como circunferencias tangentes a la recta que representa al plano secante y a las generatrices aparentes, de forma que se obtienen dos circunferencias de contacto de dichas esferas con la superficie cónica (que aparecen aquí como las rectas T1-T2 y T3-T4).

Los puntos de tangencia de las esferas con el plano de corte son los puntos F1 y F2, focos de la hipérbola.

Los puntos de tangencia con la superficie cónica representan a las circunferencias de la solución tridimensional (hemos visto que T1-T2 y T3-T4 son dos circunferencias). Los planos en que se encuentran definen las directrices de la hipérbola.

En la figura también puede verse la cónica resultante abatida sobre el papel.

Trazado, Tangencias y Cortes en la Hipérbola

Al igual que ocurría con la elipse y la parábola, existen varios métodos para trazar una hipérbola a partir de sus elementos (ejes, focos, vértices, asíntotas…), así como para encontrar sus tangentes y puntos de corte con una recta.

A continuación se muestran algunos de ellos, a título ilustrativo. En todas las construcciones se ha incluido la figura de la hipérbola con el fin de identificar correctamente los elementos de la solución.

Trazado de la Hipérbola por puntos

Se eligen varios puntos sobre el eje real (en el ejemplo, 1, 2, 3 y 4).

Para el punto 1, trazamos un arco con centro en F1 y radio A-1, y otro arco con centro en F2 y radio B-1. Ambos arcos se cortan en 2 puntos de la curva (A1-B1=AB).

Repitiendo para 2, 3 y 4 obtenemos más puntos.

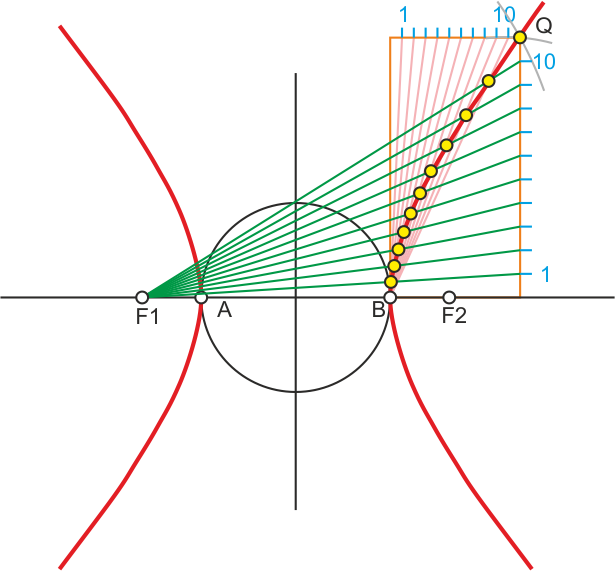
Trazado de la Hipérbola por rectas (haces proyectivos)

Por el método de los puntos (ver construcción anterior) encontramos un punto Q de la curva. Dividimos el rectángulo cuyas esquinas son B y Q en igual número de partes horizontal y verticalmente (11 partes en la figura). Se une el foco contrario con las particiones verticales, y el vértice B con las horizontales. Los puntos de corte de ambos haces de rectas son puntos de la curva.

Los puntos al otro lado de la rema y en la otra pueden obtenerse por simetría

Trazado de la Hipérbola por tangentes envolventes

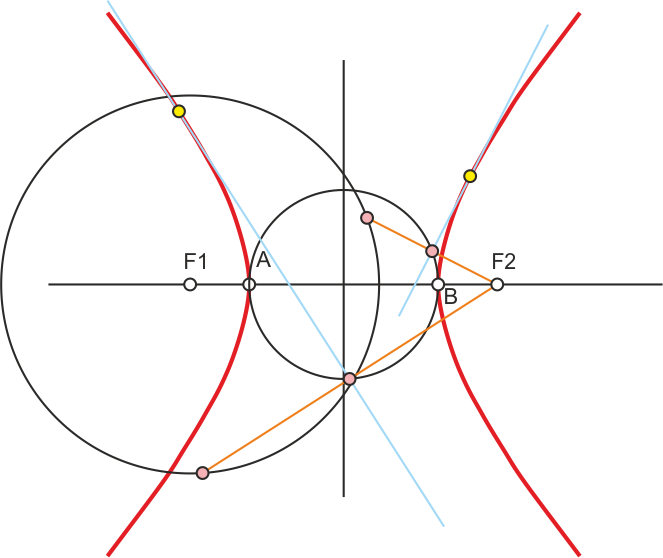
La mediatriz de una recta que une un foco con un punto de la circunferencia focal del otro foco es tangente de la curva. Además, los puntos medios de estas rectas están en la circunferencia principal.

De esta forma pueden trazarse varias tangentes para dibujar la curva por envolventes (en la figura solo se han trazado dos tangentes).

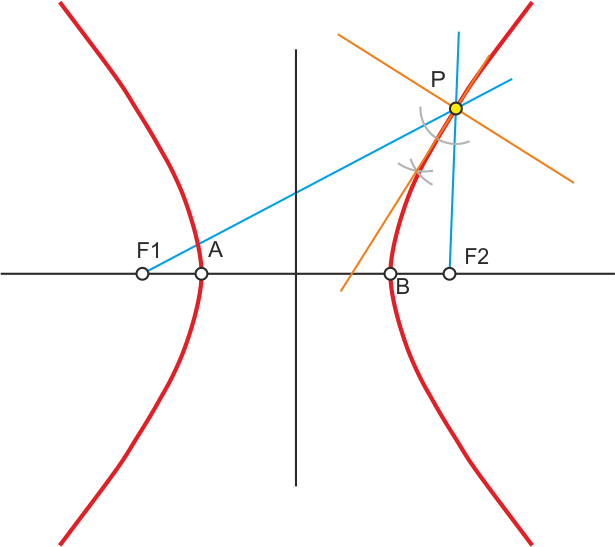
Tangente y normal a la Hipérbola por uno de sus puntos

Para encontrar la tangente por un punto P de la curva, trazamos sus radio vectores. La bisectriz interior del ángulo que forman es la tangente a la curva, y la bisectriz exterior es la normal.

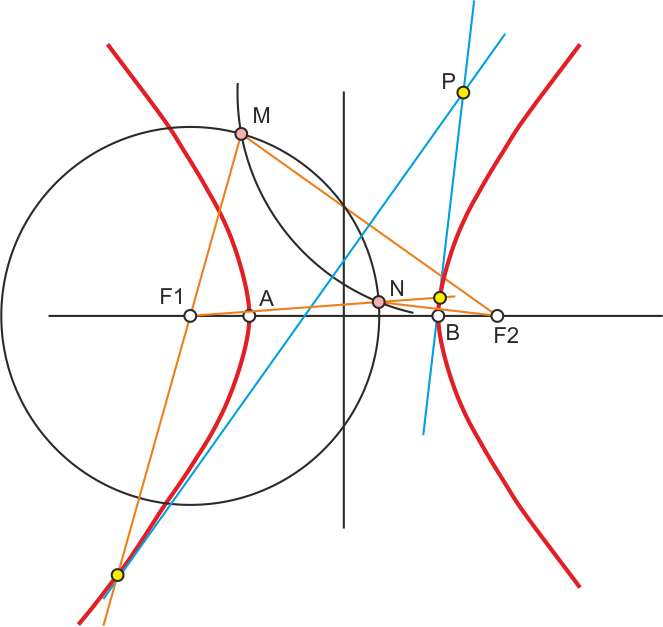
Tangentes a la Hipérbola por un punto exterior P

Trazamos la focal de F1. Con centro en P, trazamos un arco de radio PF2, que corta en M y N a la focal trazada
Las mediatrices de MF2 y NF2 son las tangentes buscadas.

Los puntos de tangencia X e Y los obtenemos al prolongar MF1 y NF1 hasta tocar a las tangentes.

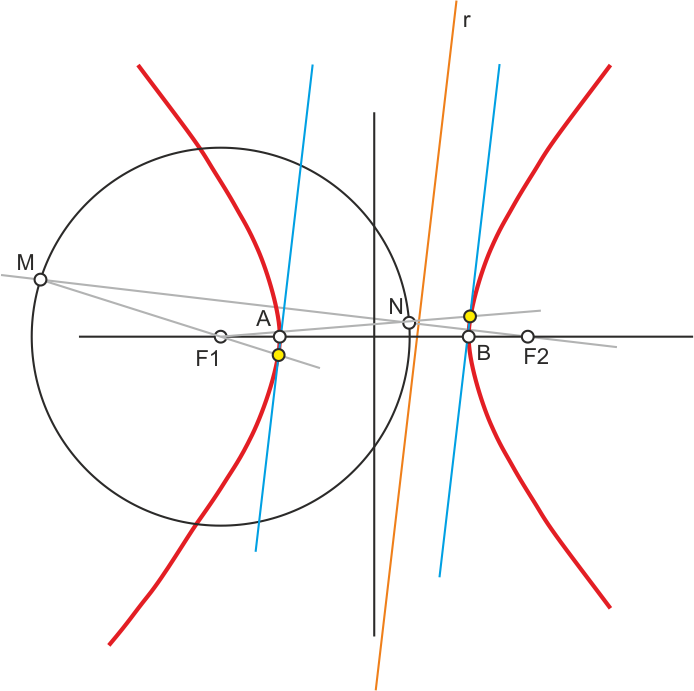
Tangentes a la Hipérbola paralelas a una dirección dada por la recta r

Trazamos la focal de F1. Desde el foco F2 trazamos una perpendicular a r, que corta a la focal anterior en los puntos M y N. Las mediatrices de MF2 y NF2 son las tangentes buscadas. Los puntos de tangencia X e Y se obtienen al unir F1 con M y N.

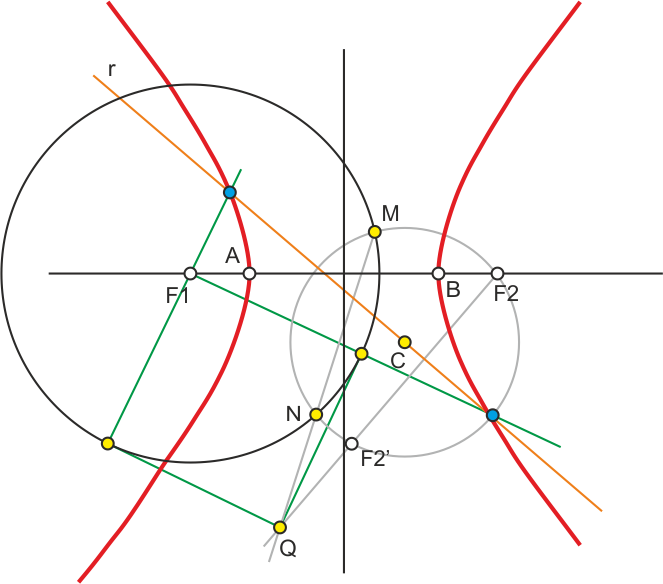
Intersección entre Hipérbola y recta secante r

Trazamos la focal del foco F1. Encontramos F2’, el simétrico de F2 respecto de la recta r. Sobre r, tomamos un punto cualquiera C y con centro en él trazamos una circunferencia de radio CF2, que cortará a la focal de F1 en los puntos M y N. Prolongamos MN y F2F2’ hasta que se corten en Q. Trazamos las tangentes desde Q hasta la focal de F1. Uniendo F1 con los puntos de tangencia obtenemos las soluciones X e Y sobre la recta r.