Relaciones métricas

El tetraedro tiene 3 magnitudes fundamentales, que son:

• La arista (a). Es la longitud de todos los lados de todos los triángulos que forman su superficie.
• La altura de la cara (hc). Es la longitud de cualquier altura de cualquier cara de la figura.
• La altura de la figura (h). Es la distancia desde un vértice hasta la cara contraria.

A partir de cualquiera de las tres magnitudes anteriores podemos encontrar las otras dos. Si es necesario puede realizarse una homotecia a una figura de cualquier tamaño para encontrar las dimensiones buscadas mediante una homotecia.

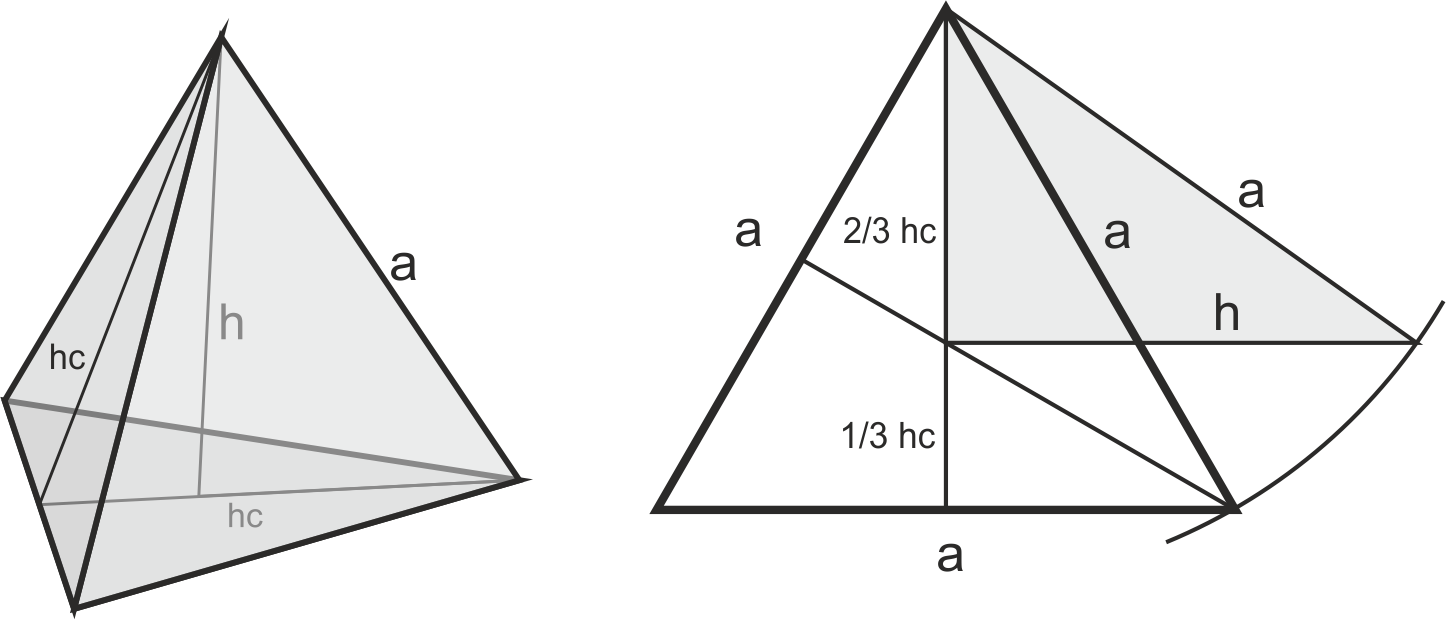
Las caras del tetraedro

Las caras del tetraedro son triángulos equiláteros, por lo que en ellas las tres alturas coinciden con las tres medianas y con las tres mediatrices. Si se representa una cara con un lado horizontal, su centro geométrico (a la vez incentro, circuncentro, ortocentro y baricentro) está a 1/3 de la altura perpendicular a ese lado (ver figura anterior).

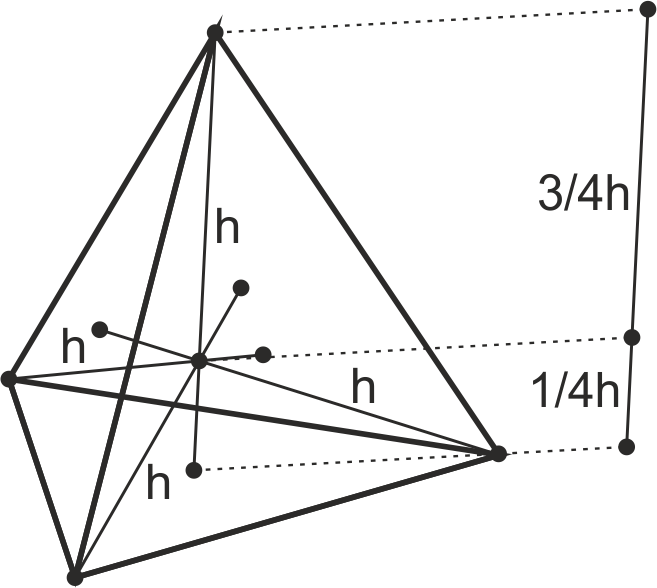
Alturas del tetraedro. Centro geométrico

La altura h de un tetraedro es la distancia entre un vértice y la cara opuesta o, lo que es lo mismo, entre un vértice y el pie de la perpendicular trazada por él a la cara opuesta. Este pie es el centro de dicha cara opuesta.

En la figura, las cuatro alturas h son iguales y se cortan en el centro geométrico espacial del tetraedro, que también es su centro de gravedad. Si se coloca el tetraedro apoyado en una cara, puede comprobarse que este centro geométrico está a 1/4 de la altura h perpendicular a esa cara.

Sección Principal

La sección principal de un tetraedro es la que se obtiene al cortarlo por un plano que pasa por una arista y por el punto medio de la arista contraria. Esta sección es un triángulo isósceles cuyo lado desigual es la arista del poliedro y cuyos lados iguales son hc. Hay tantas secciones principales como aristas, esto es, 6.

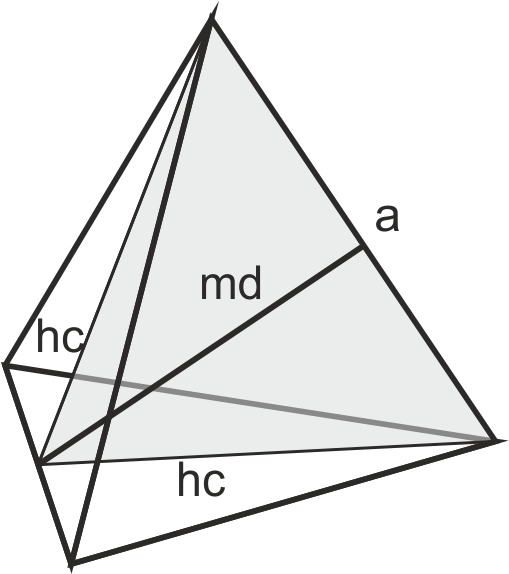
Mínima distancia entre aristas

Las aristas del tetraedro se cruzan dos a dos perpendicularmente. Si se toman los puntos medios de las aristas y se unen dos a dos se obtienen dos segmentos que constituyen las mínimas distancias entre esas aristas que se cruzan. Esta mínima distancia (md en la figura anterior) es la altura de la sección principal del tetraedro.

Ejemplos de representación de tetraedros

Tetraedro apoyado en uno de los planos de proyección

Esta posición del tetraedro es la más sencilla. Basta con representar la cara apoyada (que aparecerá en verdadera magnitud en la proyección horizontal) y elevar sobre el plano de apoyo (H en este caso) la altura h del poliedro, colocando el cuarto vértice en la vertical sobre el centro de la cara apoyada. Este caso es extensible a tetraedros apoyados en planos horizontales y frontales cualesquiera.

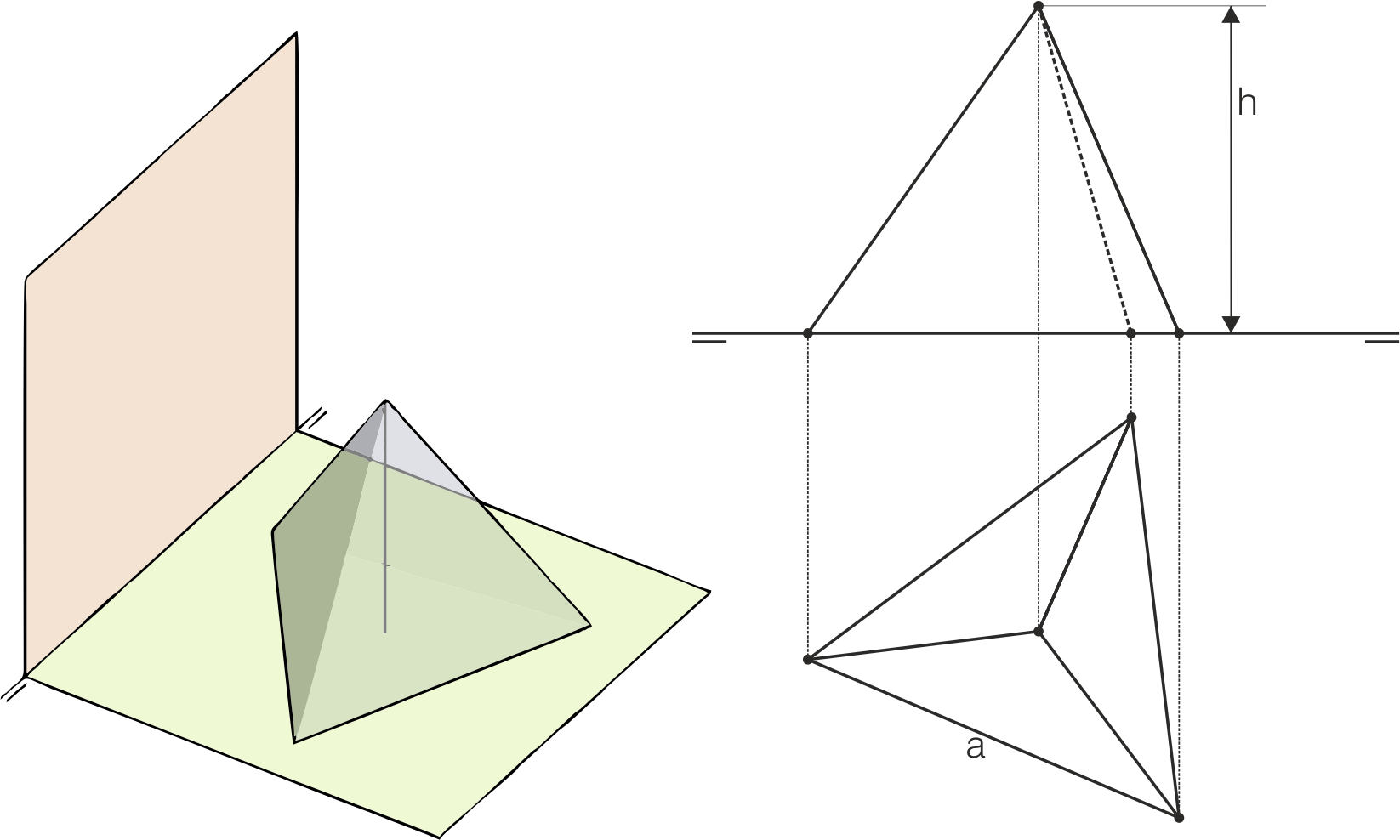
Tetraedro con dos aristas horizontales

Cuando el tetraedro tiene dos aristas horizontales (en la figura, además, una pertenece a H), el contorno de la proyección horizontal del poliedro es un cuadrado, del cual sabemos que la diagonal es igual a la artista del poliedro. La altura de la proyección vertical viene dada por la mínima distancia (md) entre dos aristas paralelas.

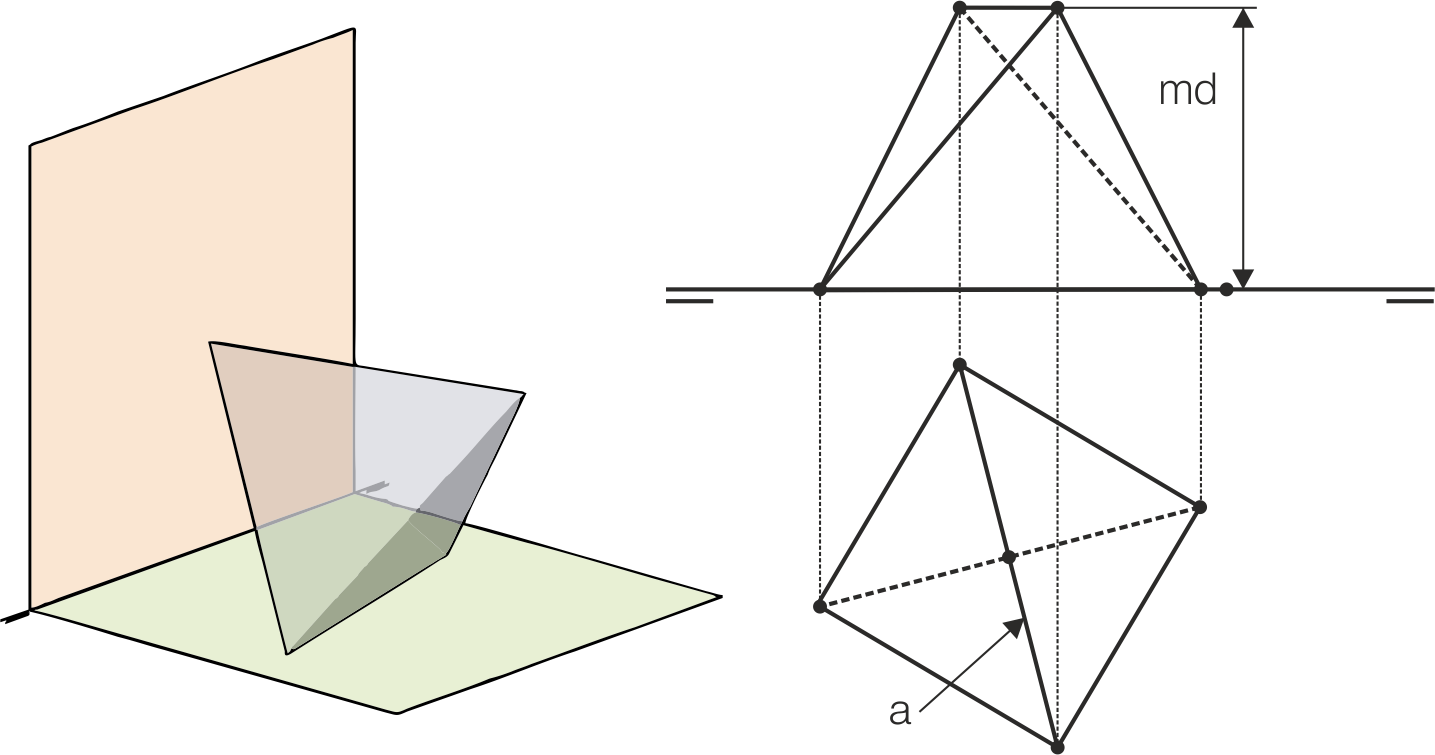
Tetraedro apoyado en un plano proyectante

En general, para dibujar un tetraedro apoyado en un plano, se debe dibujar sobre el plano la cara contenida en él (abatiendo el plano si es necesario) y, mediante una perpendicular por su centro, se encuentra el cuarto vértice con la altura h adecuada. En este caso, como el plano de apoyo es proyectante, vemos esta altura en verdadera magnitud.

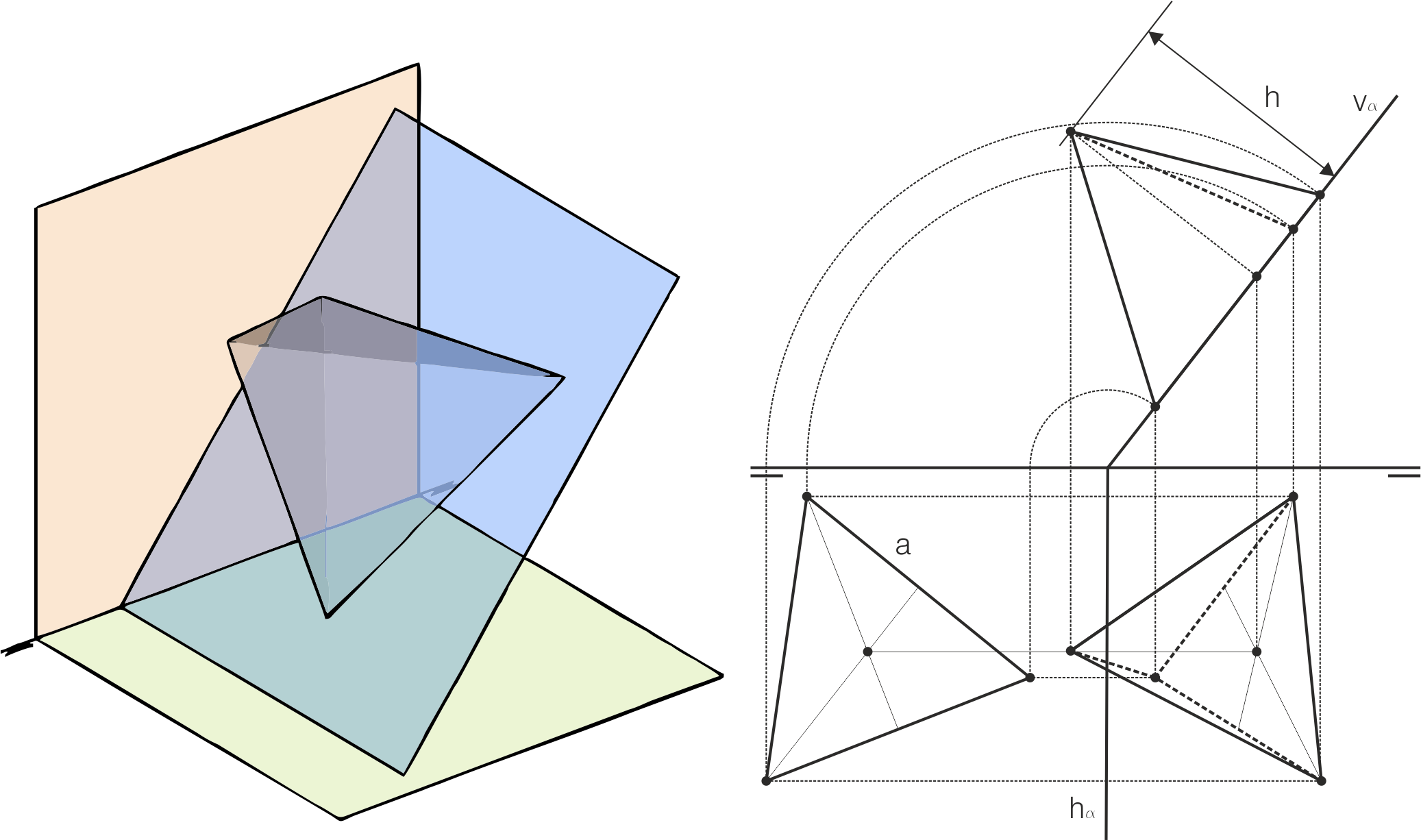
Tetraedro apoyado en un plano oblicuo

Como solución general para cualquier plano, debemos llevar sobre la perpendicular por el centro geométrico de la cara apoyada en él la distancia, en sus dos proyecciones, que corresponda a la altura del tetraedro.

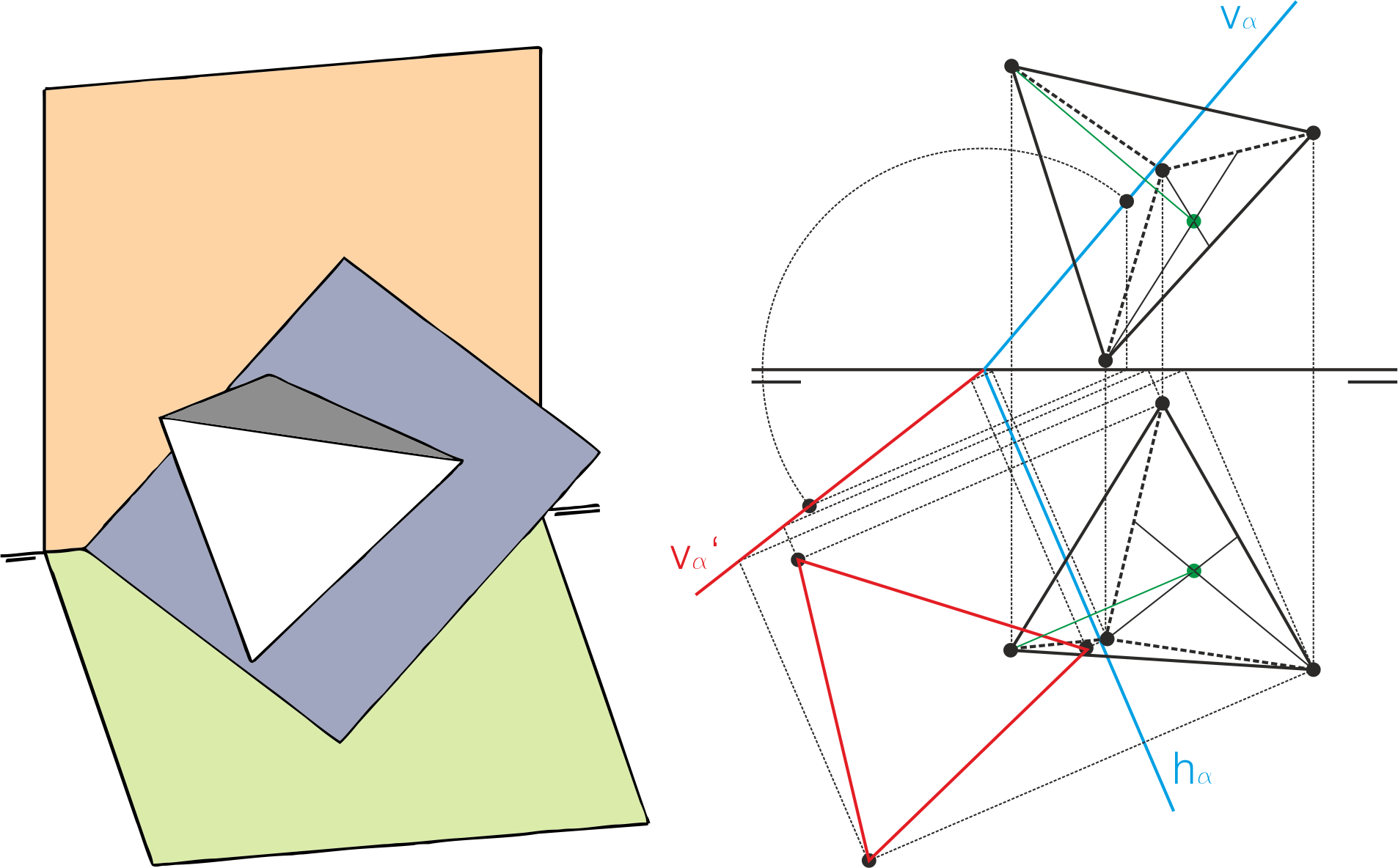
Tetraedro a partir de la sección principal

Si lo que tenemos que localizar en un plano es la sección principal del tetraedro, que contiene a dos de los vértices del mismo, podemos encontrar los otros dos vértices llevando sobre la perpendicular al plano por el tercer punto de la sección principal (el punto medio de la arista perpendicular) distancias de a/2 a ambos lados del plano.

Secciones planas del tetraedro

Como norma general, para hallar la sección que un plano produce en un poliedro, se debe cortar ese plano con todas las aristas del mismo. Los puntos de corte, unidos, formarán un polígono contenido en el plano de corte.

En un tetraedro, un plano secante puede cortar 3 ó 4 aristas. En el primer caso, el polígono obtenido es un triángulo y en el segundo, un cuadrilátero.

En los siguientes ejemplos se ilustran diferentes secciones planas. Se han obviado los trazados auxiliares (cortes de recta y plano, horizontales del plano para trasladar puntos, etc…) para dar más claridad a las soluciones.

Sección por un plano horizontal

Tenemos un tetraedro apoyado en H y cortado por un plano horizontal. La sección es un triángulo equilátero que vemos en verdadera magnitud en la proyección horizontal. El caso análogo es el plano apoyado en V y cortado por un plano frontal.

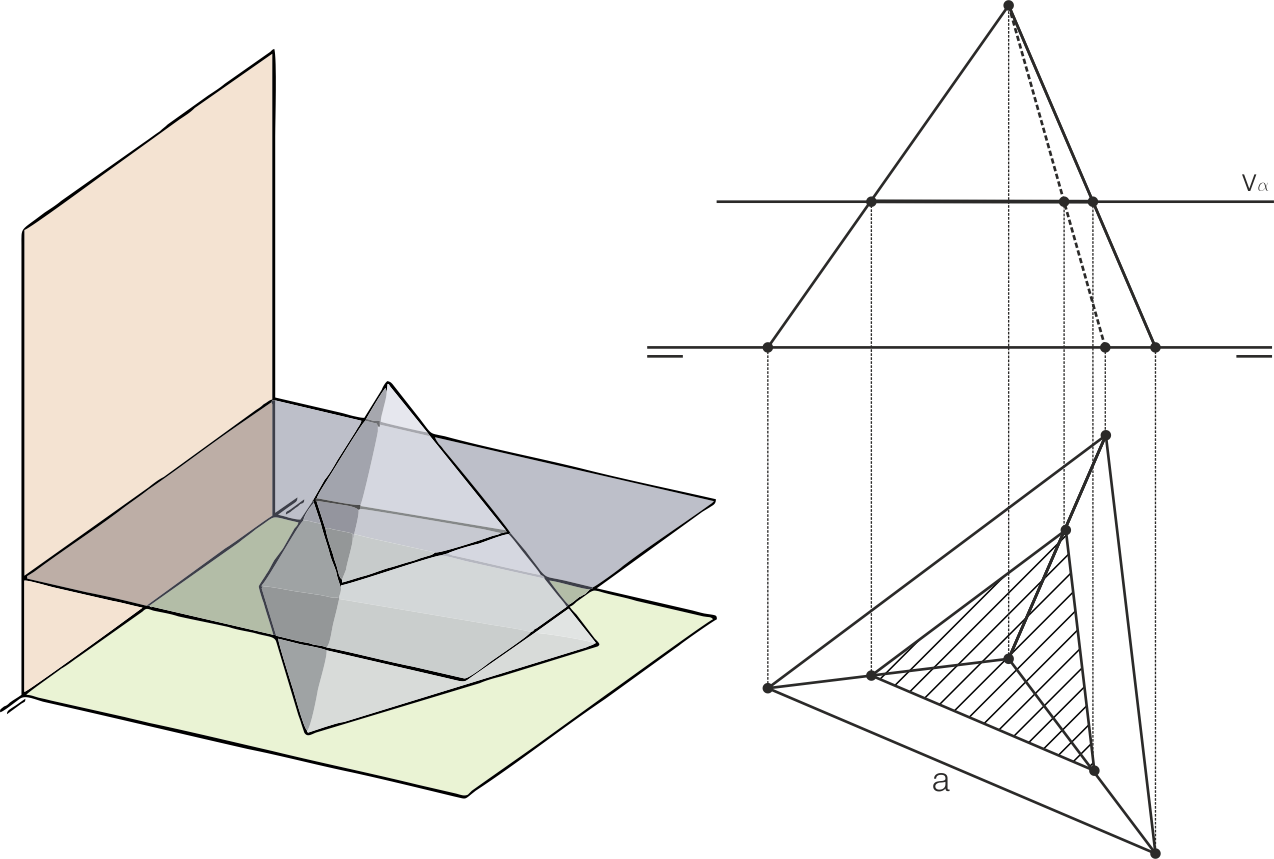
Sección por un plano proyectante

En este caso, el tetraedro está apoyado en H y es cortado por plano proyectante vertical. Si la traza horizontal del plano corta a la base, la sección es un cuadrilátero, y en caso contrario (como en el ejemplo), la sección es un triángulo. Su trazado también es sencillo, ya que en podemos encontrar de forma inmediata la proyección vertical de la sección. Sin embargo, necesitaremos abatir el plano de corte para ver dicha sección en verdaderas dimensiones (este abatimiento no se ha incluido).

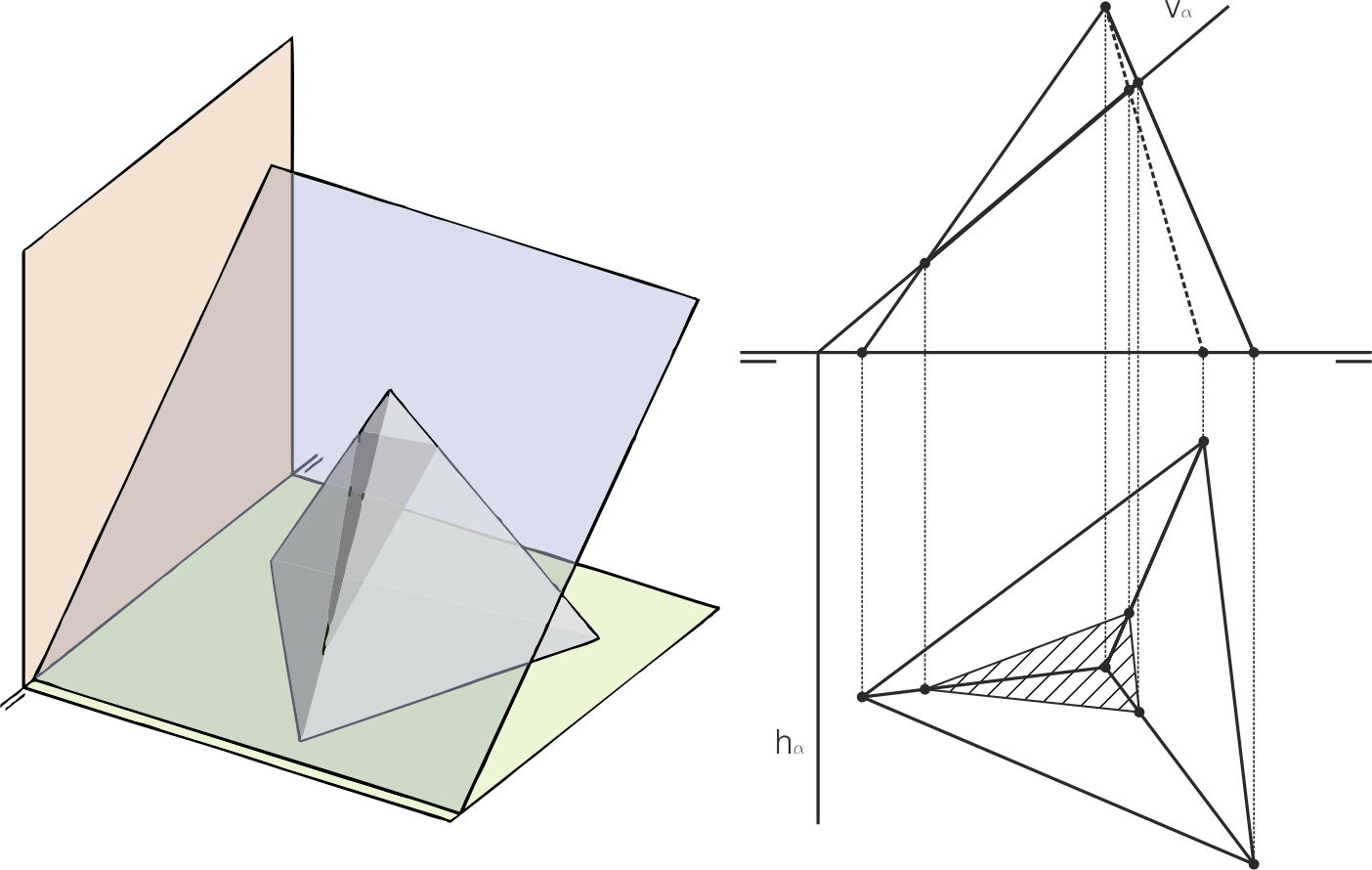
Sección por un plano oblicuo

Igual que en caso anterior, si la traza horizontal del plano corta a la base, la sección es un cuadrilátero, y en caso contrario es un triángulo. En el ejemplo, como la traza horizontal del plano de corte no toca la cara de apoyo, solo hemos cortado las tres aristas levantadas para encontrar la sección. Para ver la sección en ver-dadera magnitud hay que abatir el plano (no se ha incluido esta construcción).

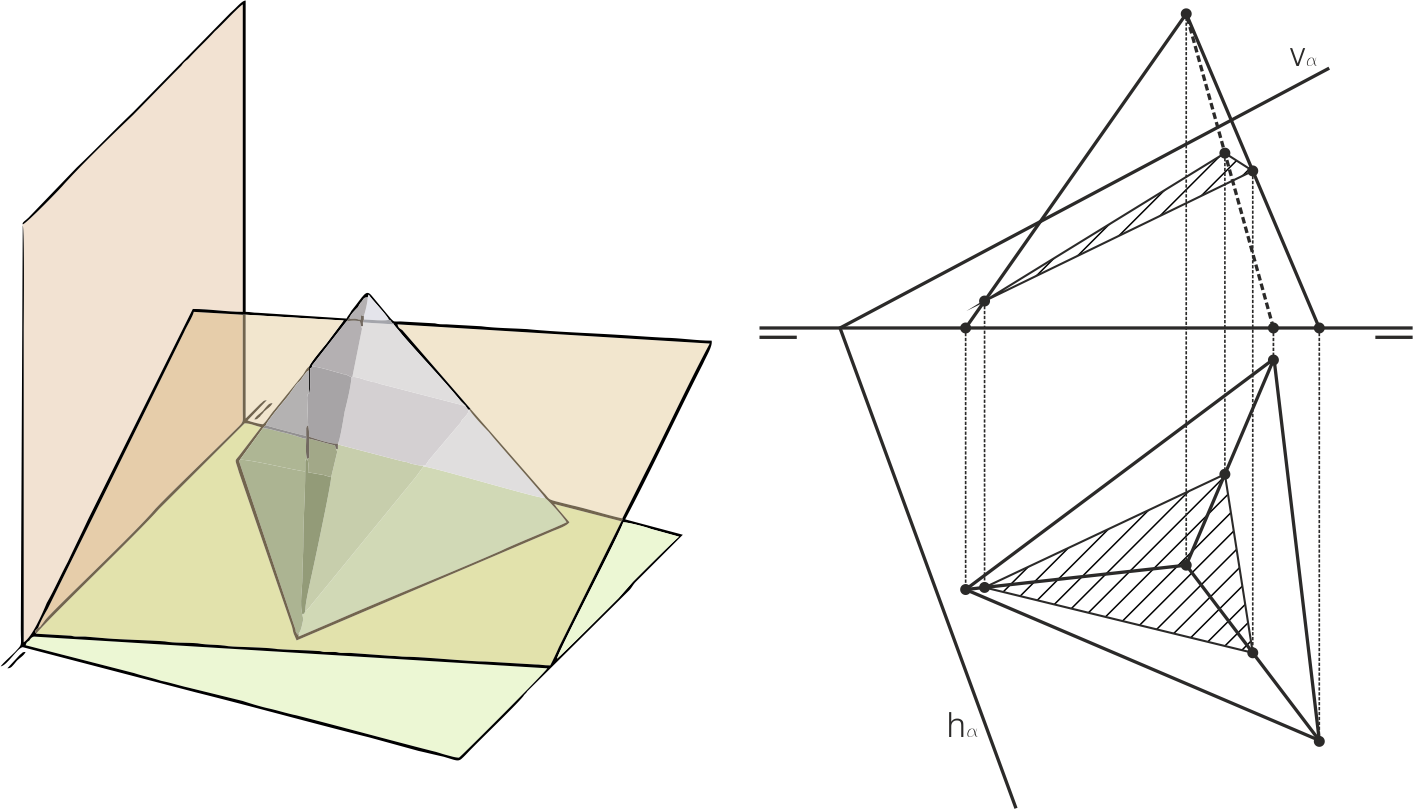
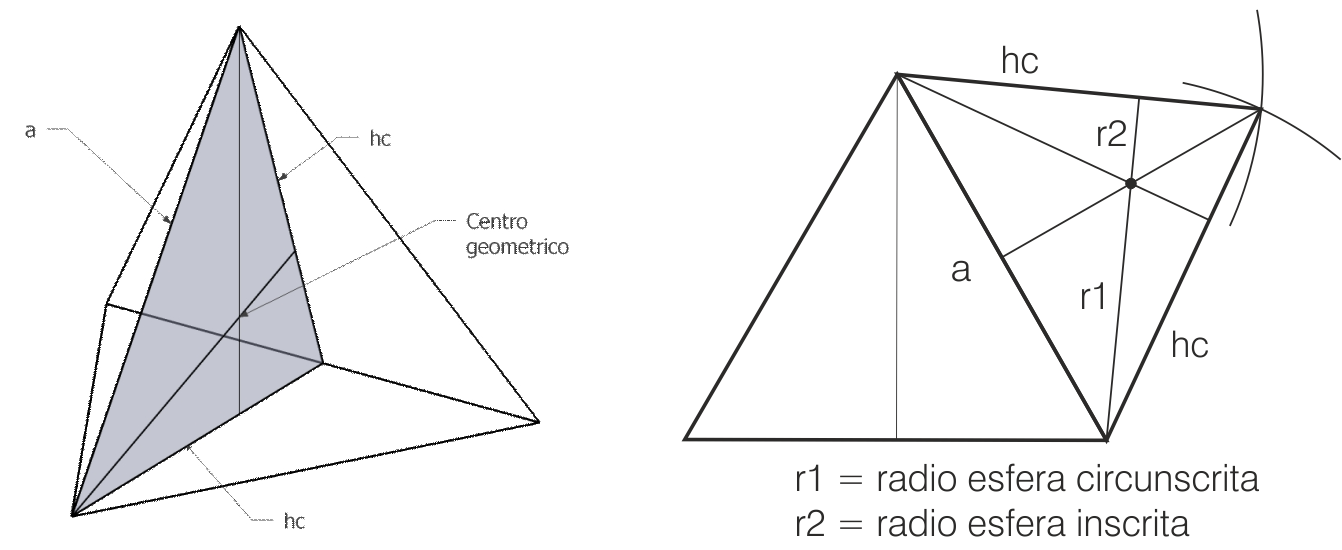
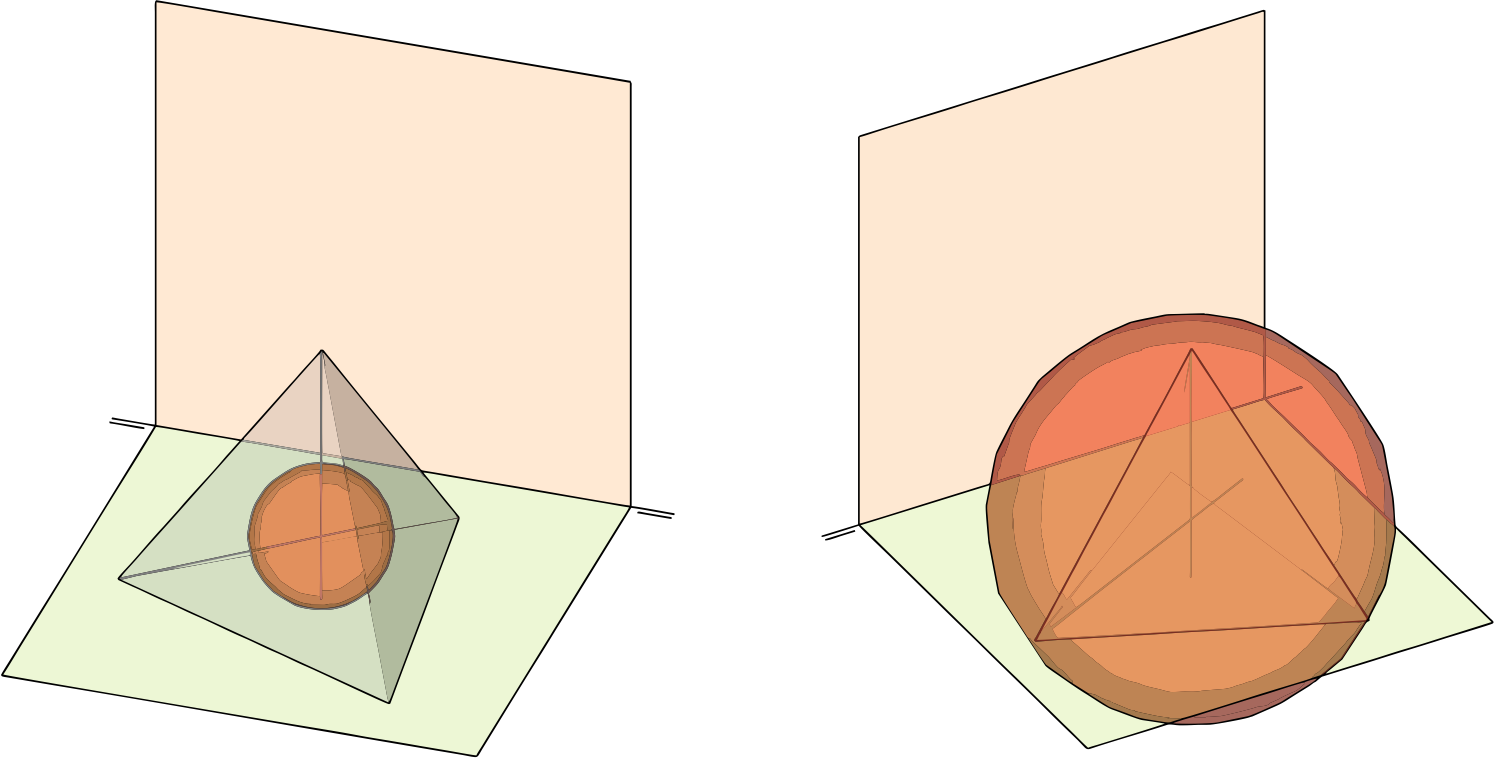
Esferas inscrita y circunscrita

La esfera inscrita al tetraedro es la tangente interior a sus cuatro caras, y su centro es el centro geométrico del tetraedro.

La esfera circunscrita al tetraedro es la que pasa por sus cuatro vértices, y su centro también es el cen-tro geométrico del poliedro.

Los radios de ambas pueden extraerse a partir de las medidas del triángulo de la sección principal.

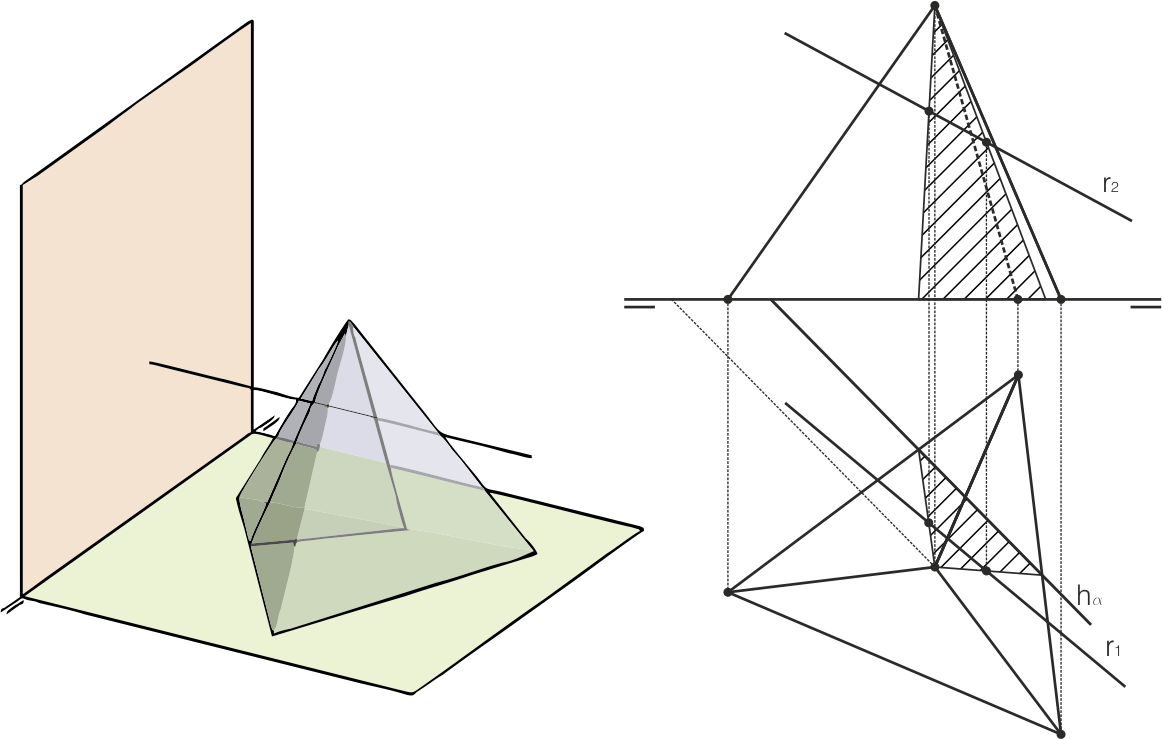
Intersección con una recta

El procedimiento general para hallar la intersección de una recta con un sólido es contener la recta en un plano, cortar éste con el sólido, y finalmente hacer la intersección de la recta con la figura obtenida en esa sección.

En el caso del tetraedro, el plano auxiliar más conveniente es aquel que pasa por el vértice superior, ya que determinará una sección triangular en el tetraedro sumamente fácil de trazar. Para encontrarlo (esta construcción se ha obviado en la figura) se eligen dos puntos cualesquiera de la recta, que junto con el vértice superior definen el plano (en este ejemplo encontramos únicamente su traza horizontal, la vertical no nos hace falta).

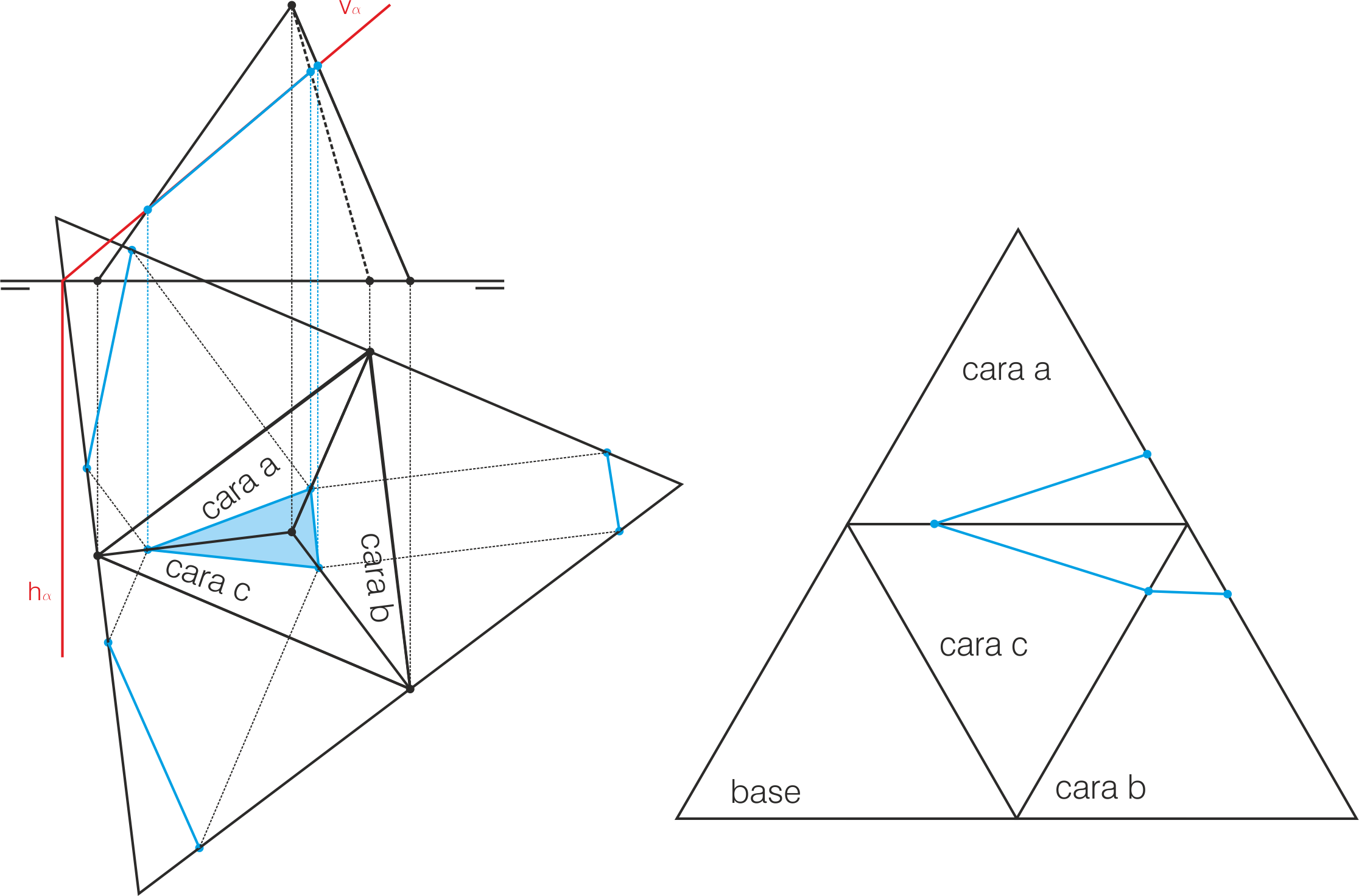
Desarrollo del Tetraedro. Transformada de la Sección

El desarrollo de un poliedro consiste en dibujar sobre un plano todas sus caras, mediante una sucesión ordenada, de tal forma que se pueda obtener el poliedro realizando dobleces por las líneas comunes. El desarrollo de un tetraedro está compuesto por cuatro triángulos equiláteros adosados, correspondientes a las caras del poliedro.

Realizar la transformada de la sección consiste en llevar a ese desarrollo el contorno de la sección ob-tenida al intersecar el cuerpo con un plano o con otro cuerpo.

En la figura siguiente, se ha trazado la transformada de una sección plana por un plano proyectante. En la proyección horizontal hemos abatido las 3 caras inclinadas, junto con los puntos de la sección. En la figura de la derecha hemos dibujado otro desarrollo diferente, y sobre él hemos trazado la transformada.