Las transformaciones geométricas planas son operaciones que relacionan dos figuras geométricas en el plano a través de ciertas propiedades.

Estas transformaciones también pueden entenderse como las relaciones geométricas, basadas en ciertas propiedades particulares cada una de ellas, que vinculan a dos figuras en el plano.

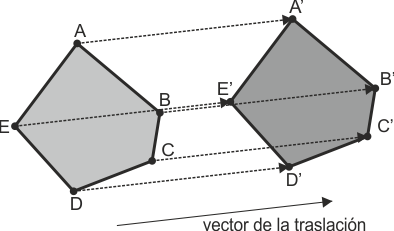
La traslación es una transformación geométrica plana consistente en desplazar cada punto (y por tanto cada arista) de una figura según una dirección, sentido y distancia fijos. Estos tres datos conforman el denominado vector de la traslación.

En una traslación, las figuras inicial y final guardan relación de igualdad.

El producto de dos traslaciones es otra traslación, cuyo vector es la suma de los dos vectores de ambas traslaciones.

La traslación suele usarse como paso final para situar figuras resultado de problemas geométricos que deben cumplir determinadas condiciones de posición. A continuación se detallan varios ejemplos.

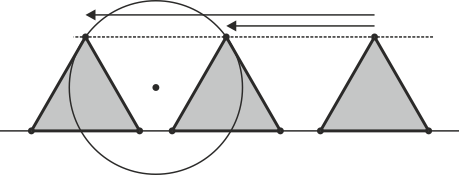
Ejemplo 1.- Dada una circunferencia de 2 cm de radio y una recta que está a 1 cm de su centro, encontrar un triángulo equilátero de lado 2,5 cm que tenga un lado sobre la recta y el vértice opuesto en la circunferencia. Dibujamos primero el triángulo apoyado en recta (primera condición) y luego aplicamos una traslación para que, sin dejarse de cumplir la primera condición, se cumpla la segunda (hay dos soluciones).

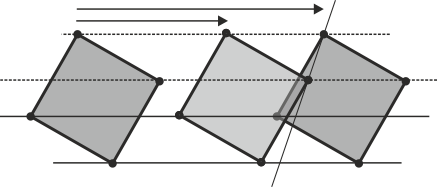
Ejemplo 2.- Dibujar un cuadrado que tiene dos de sus vértices en dos paralelas dadas y otro en otra oblicua que las corta. Dibujamos el cuadrado con dos vértices en las rectas (primera condición) y después aplicamos una traslación para que, sin dejarse de cumplir la primera condición, se cumpla la segunda (hay dos soluciones).

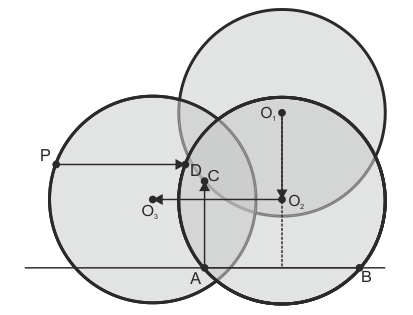
Ejemplo 3.- Dado un punto P y una recta r a 2 cm de distancia de él, dibujar una circunferencia de radio 2 cm que pase por el punto e intercepte a la recta en una cuerda de 3 cm. Dibujamos una circunferencia de radio 2 centrada en un punto cualquiera O1. Centrado en la perpendicular a la recta por O1 dibujamos el segmento de 3 cm, que proporciona los puntos A y B. Llevamos A sobre la circunferencia dando C. Aplicando la traslación inversa al vector AC obtenemos O2. Para colocarlo en su posición final, llevamos P sobre la circunferencia y aplicamos una nueva traslación, esta vez inversa al vector PD y obteniendo O3 (hay una segunda solución).