Introducción
En una sección plana a un cono, si β, el ángulo que forman el eje del cono y el plano que corta a la superficie cónica, es mayor que el semiángulo cónico α, la curva intersección es una curva cerrada, denominada elipse.
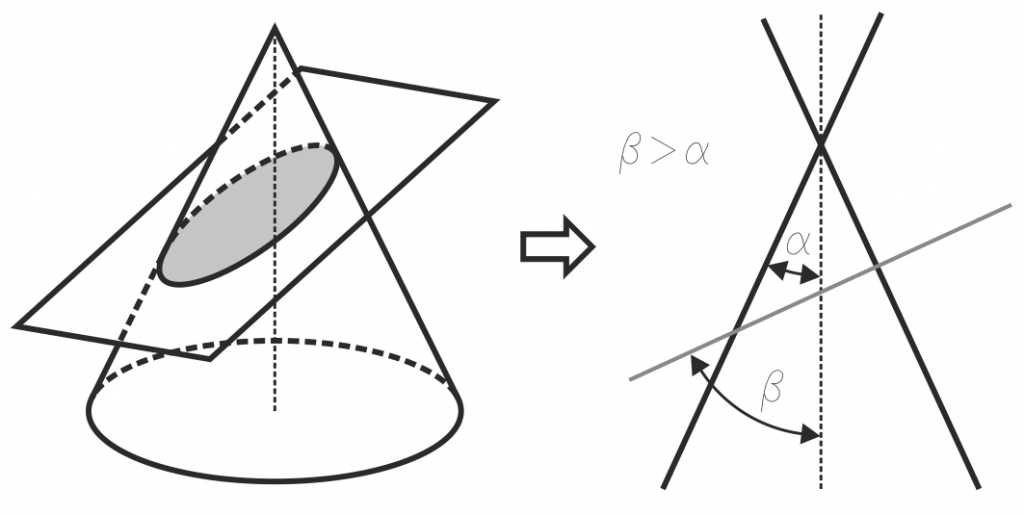
Se pueden dar elipses degeneradas (casos particulares de elipses) en estos casos:
- Si el plano es perpendicular al eje de revolución del cono, en cuyo caso la elipse es una circunferencia.
- Si el plano pasa por el vértice, en cuyo caso la curva se degenera en un punto.
Elementos de la Elipse
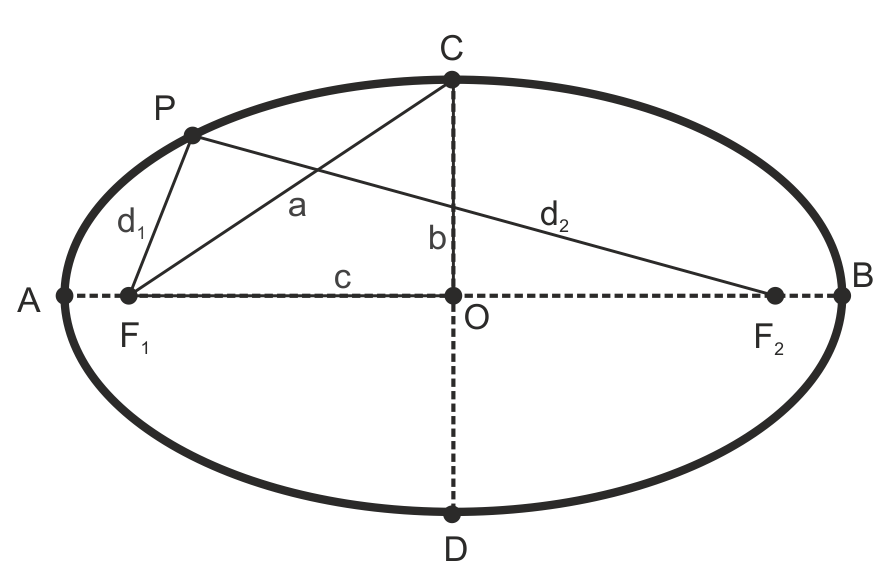
En el dibujo de arriba, los elementos de la elipse son:
- A, B, C, D = Vértices
- O = Centro
- F1 y F2 = Focos
- AB = Eje mayor o focal
- CD = Eje menor o secundario
Las distancias notables en la elipse son
- AB = 2a = Longitud del eje mayor
- CD = 2b = Longitud del eje menor
- F1F2 = 2c = Distancia focal
- d1 y d2 = Radiovectores del punto P (segmentos que lo unen a los focos)
- CF1 = CF2 = a
Se cumplen las siguientes propiedades
- d1 + d2 = 2a (constante para todos los puntos)
- b2 + c2 = a2 (Pitágoras)
Excentricidad
Métricamente, un cónica (nos referiremos así a las curvas cónicas), puede definirse como el lugar geométrico de los puntos P del plano cuya razón o cociente entre una distancia a un punto fijo llamado foco (F) y a una recta fija llamada directriz (M) es constante. Esta constante se denomina excentricidad de la cónica.
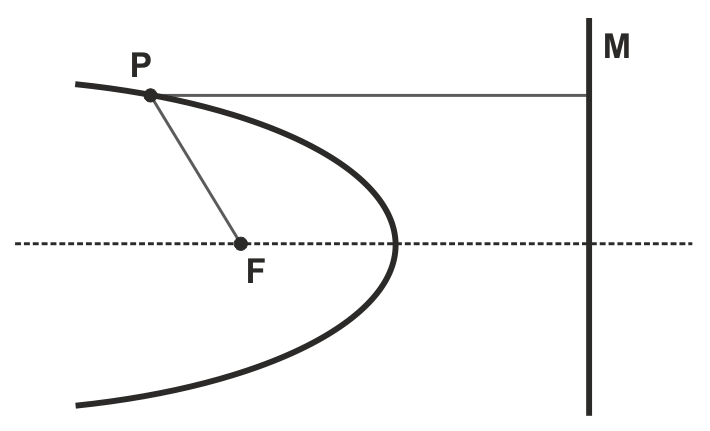
- Si e < 1 -> se trata de una elipse
- Si e = 1 -> se trata de una parábola
- Si e > 1 -> se trata de una hipérbola
En el caso de la elipse, la excentricidad equivale al cociente entre el eje mayor (2a) y la distancia focal (2c), y es siempre menor que 1. Cuanto menor sea este valor más “redonda” será la elipse, es decir más se aproximará a una circunferencia.
La Elipse como lugar geométrico
Los puntos de la elipse tienen una propiedad que permite definirla como el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos (llamados focos) es constante.
Esa constante es igual la longitud del eje mayor de la elipse (AB).
La elipse también puede definirse como el lugar geométrico de los centros de las circunferencias tangentes a otra dada que pasan por un punto fijo interior a ésta. Y también es el lugar geométrico de los puntos que equidistan de una circunferencia y de un punto interior a ésta.

Ecuación matemática de la Elipse
Considerando el centro de la elipse como el origen de coordenadas (0,0), y considerando que las coordenadas de un punto P son (x, y), en la figura de la elipse de la página anterior se cumple:
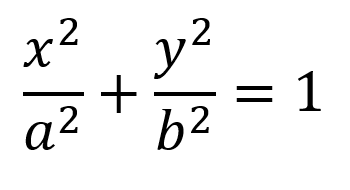
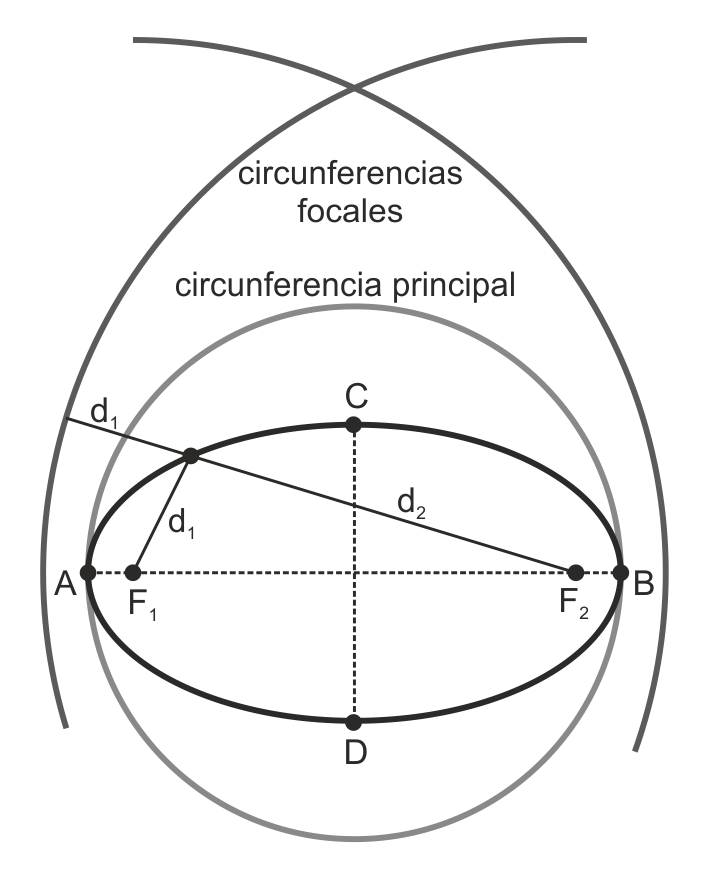
Más Elementos de la Elipse
Las circunferencias focales de la elipse tienen como centro los focos y como radio 2a (en la figura, AB = d1 + d2 = 2a).
La circunferencia principal de la elipse tiene como centro el centro de la elipse y como diámetro 2a (AB).
Las directrices de la elipse (que no se han representado en el dibujo) son las rectas polares de los focos respecto a la circunferencia principal.
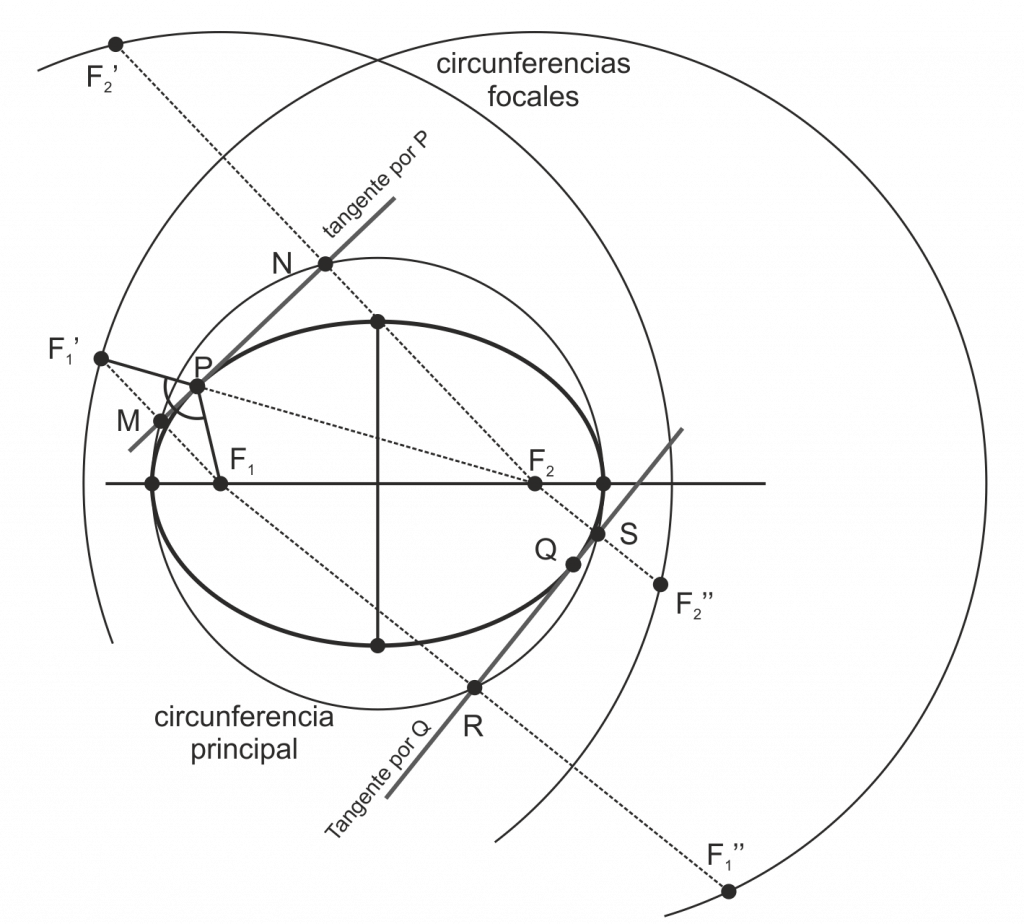
Propiedades especiales de la Elipse
La circunferencia focal de un foco (F2 en la figura) es el lugar geométrico de los puntos simétricos del otro foco (F1 en la figura) con respecto a cualquier tangente a la elipse (en la figura, la tangente por P).
La circunferencia principal es el lugar geométrico de los puntos (M en la figura) que, estando en las tangentes, son los intermedios entre un foco (F1 en la figura) y su simétrico (F1‘) con respecto a esa tangente a la elipse, o sea, es el lugar geométrico de los pies de las perpendiculares a las tangentes desde los focos.
El punto (P en la figura), punto de contacto de una tangente con una elipse, está alineado con un foco (F2 en la figura) y el simétrico del otro con respecto a esa tangente (F1’). La tangente es bisectriz del ángulo formado por P, F1 y F1’.
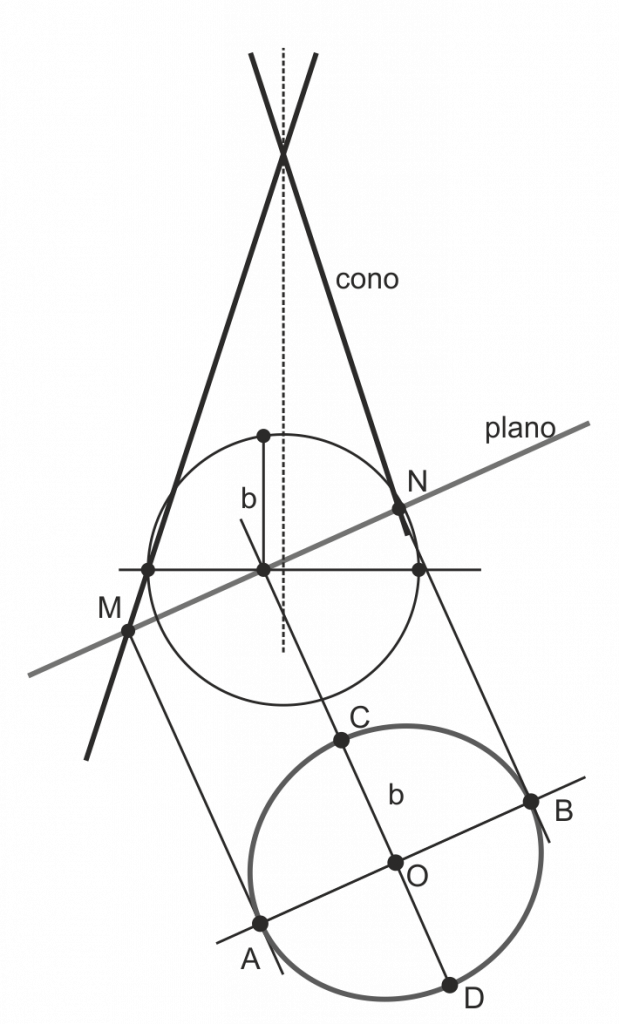
Determinación de los elementos de la Elipse a partir del plano de corte con el cono
Si dibujamos la figura de la superficie cónica cortada por el plano de forma que éste quede perpendicular al papel, podemos determinar los ejes de la elipse obtenida en dicho corte, sin necesidad de encontrar los focos:
- Los puntos de corte M y N equivalen al diámetro máximo de la curva, esto es, al eje mayor AB. Construimos la figura abatida y dibujamos directamente AB.
- El punto medio de MN equivale al centro de la elipse O.
- Si por este punto trazamos una recta perpendicular al eje del cono podemos considerar que es la traza de un plano que lo corta en una circunferencia. Esta circunferencia la representamos abatida.
- La intersección de esta circunferencia con la elipse debe ser un segmento que se corresponde con el eje menor de la elipse, asi que la distancia b obtenida sobre la circunferencia es el semieje menor, que ya podemos trasladar a la figura abatida.
- Si es necesario, podemos obtener los focos a partir de los ejes.
Teorema de Dandelin en la Elipse
El Teorema de Dandelin dice que, dada una superficie cónica y un plano que la secciona formando una curva cónica, siempre se pueden dibujar una o dos esferas (una en el caso de la parábola) tangentes interiores a la superficie cónica y a su vez tangentes al plano de corte.
El Teorema de Dandelin aplicado a la elipse enuncia que los puntos de tangencia F1 y F2 de las esferas con el plano de corte son los focos de la cónica, y los planos que contienen a las circunferencias de contacto de las esferas con la superficie cónica intersectan al plano de corte en dos rectas d1 y d2, que son las directrices de la elipse.
En la figura de abajo se representa la interpretación plana del Teorema de Dandelin en la Elipse, mediante una vista en la que el plano de corte queda perpendicular al papel, y se representa por una recta. El plano secante corta a las generatrices aparentes (las más exteriores) en los puntos A y B, que serán vértices del eje mayor de la elipse.
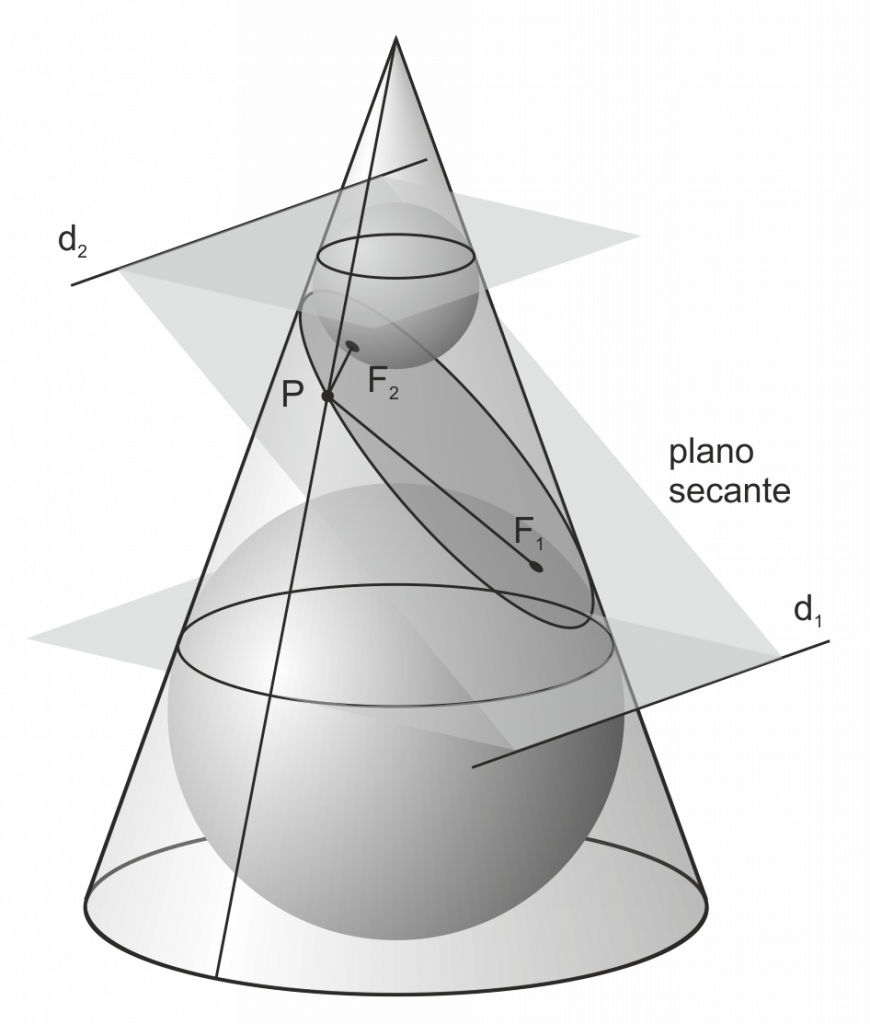
En esta interpretación las esferas tangentes aparecen como circunferencias tangentes a la recta que representa al plano secante y a las generatrices aparentes, de forma que se obtienen dos circunferencias de contacto de dichas esferas con la superficie cónica (que aparecen aquí como las rectas T1-T2 y T3-T4).
Los puntos de tangencia de las esferas con el plano de corte son los puntos F1 y F2, que serán los focos de la elipse. Los puntos de tangencia con la superficie cónica representan a las circunferencias de la solución tridimensional (hemos visto que T1-T2 es una circunferencia y T3-T4 es la otra). Los planos en los que se encuentran estas circunferencias definen las directrices d1 y d2 de la elipse.
En la figura también puede verse la cónica resultante abatida sobre el papel. El eje menor puede obtenerse fácilmente a partir del eje mayor y los focos.
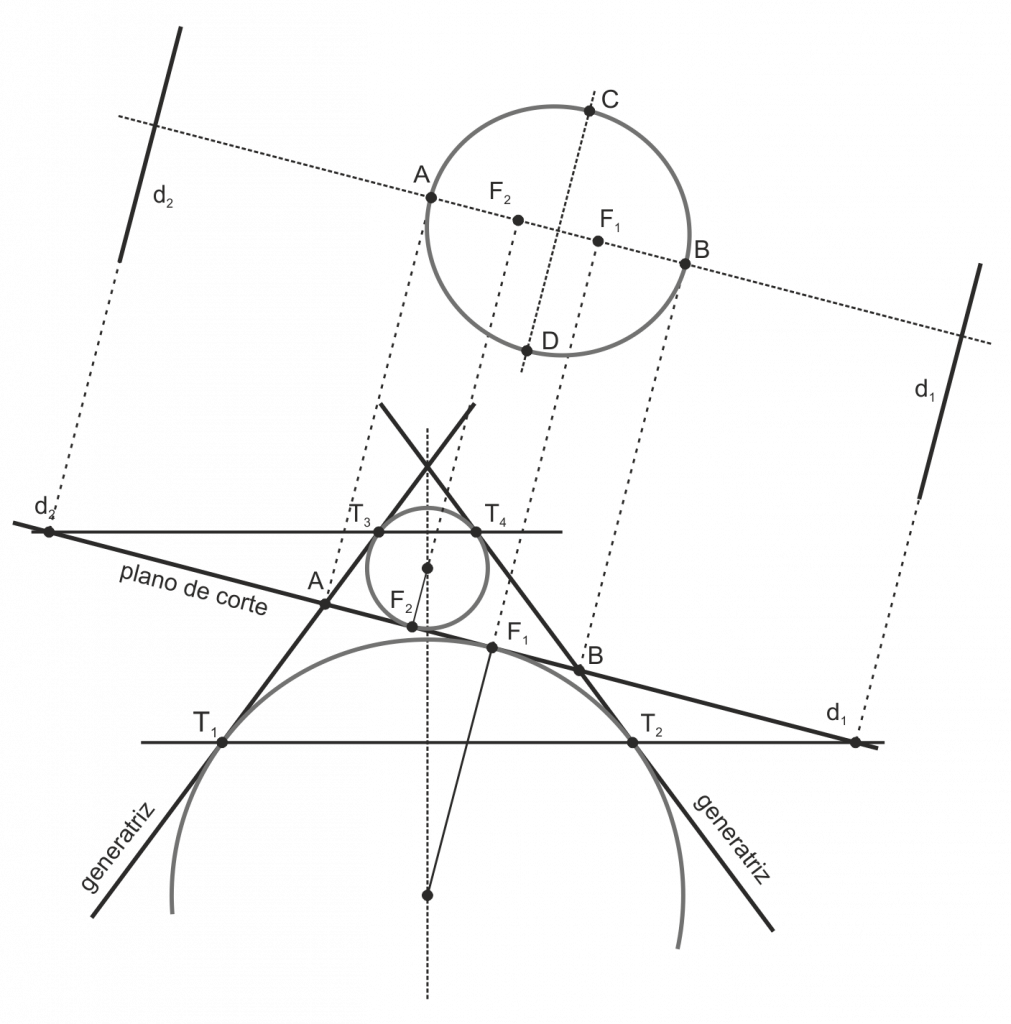
Diámetros conjugados en la Elipse
Dado un diámetro de la elipse (una recta que pasa por su centro), su conjugado es aquel que se obtiene de unir los centros de las cuerdas paralelas al primero.
Los ejes son el único par de diámetros conjugados perpendiculares.
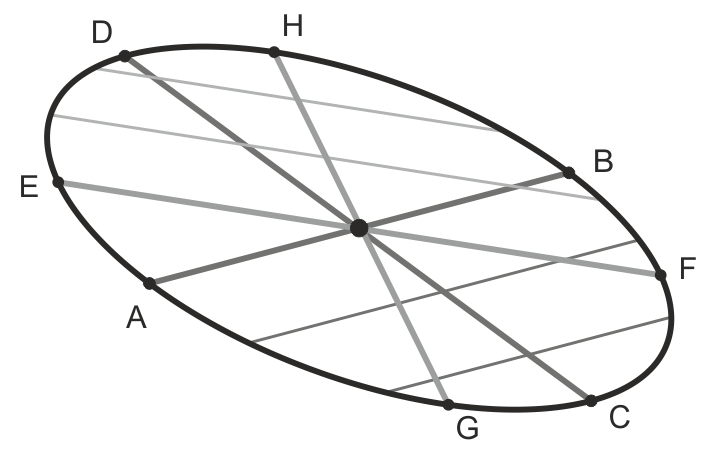
El Teorema de Apolonio dice que la suma de los cuadrados de dos pares de diámetros conjugados cualesquiera (incluso los ejes) es constante (en la figura, AB2 + CD2 = DF2 + GH2 = constante).
Obtención de los ejes a partir de un par de diámetros conjugados
Partiendo de dos diámetros conjugados de la elipse (EF y GH en la figura) podemos encontrar los ejes siguiendo este método:
- Giramos el vértice E alrededor del centro de la elipse 90º hasta obtener el punto J.
- Trazamos el círculo de diámetro JG, a cuyo centro llamamos K
- Unimos el centro de la elipse con K y prolongamos, obteniendo sobre el círculo anterior M y N
- Trazamos las rectas NG y MG, que van a marcar las direcciones de los ejes (que dibujamos trazando paralelas a ellas por el centro de la elipse)
- El semieje menor es la distancia entre el centro de la elipse y el punto N, y el semieje mayor la distancia entre el centro y el punto M (se han trazado círculos para transportar los puntos a los ejes, dando los vértices de la elipse, A, B, C y D)

Trazado, Tangencias y Cortes en la Elipse
Existen varios métodos para trazar una elipse o para encontrar sus tangentes, dados sus elementos. A continuación se detallan algunos de ellos. Aunque algunos de ellos no es muy práctico utilizarlos, se incluyen a título ilustrativo, toda vez que además ilustran las propiedades de la curva.
En todas las figuras se ha incluido la figura de la elipse con el fin de identificar correctamente los elementos de la solución.
Junto a las figuras se incluyen unos códigos QR que enlazan a páginas de internet con animaciones en formato Flash y en GIF animado que detallan paso a paso todas las construcciones. Estas animaciones pueden verse con cualquier PC o dispositivo móvil con acceso a internet.
Trazado de la Elipse por puntos
Dados los ejes y focos de la elipse, para trazarla por puntos seguimos estos pasos:
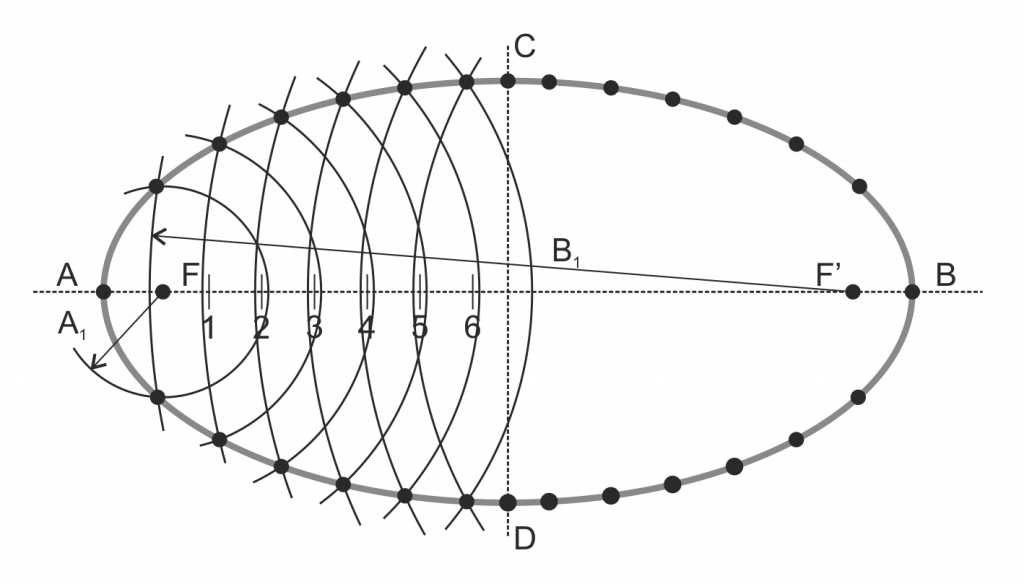
- Sobre el eje mayor, elegimos varios puntos al azar, preferentemente equitativamente repartidos (en la figura, 1 a 6). Para el punto 1, se cumplirá A1+B1=2a; para el punto 2, se cumplirá A2+B2=2a; etc…
- Con centro en un foco (F) y radio A1 trazamos un arco. Con centro en el otro y radio B1 trazamos otro. Los dos puntos de corte de ambos arcos por definición pertenecen a la elipse, ya que sus radiovectores son A1 y B1 y hemos visto que A1+B1=2a
- Repetimos la operación para cada uno de los puntos 2 a 6
- Si hemos elegido puntos a un lado del eje (como en el ejemplo) el resto puede obtenerse por simetría
Trazado de la Elipse por rectas o haces proyectivos
Dados los ejes de la elipse:
- Trazamos un rectángulo en uno de los cuadrantes de la elipse.
- Lo dividimos en varias partes (tanto en horizontal como en vertical) y numeramos los puntos intermedios.
- Unimos el vértice C (opuesto al cuadrante del eje menor) con las divisiones horizontales, y el D (el contrario) con las divisiones verticales.
- Cortando los haces trazados de igual número obtenemos los puntos de la elipse en ese cuadrante.
- El resto de puntos puede obtenerse por simetría.
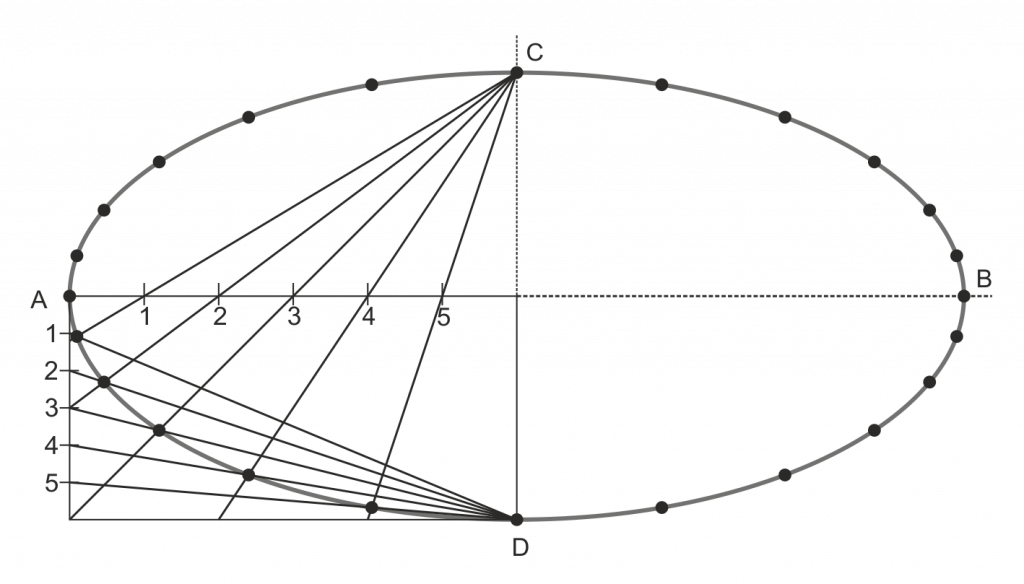
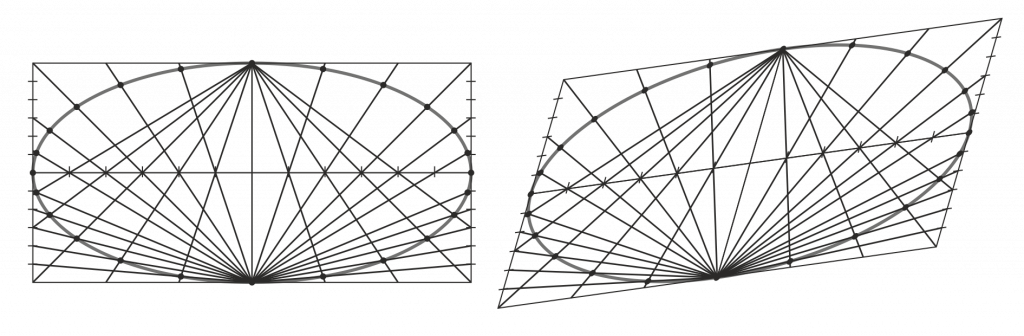
Este método también puede aplicarse si en lugar de los ejes disponemos de un par de diámetros conjugados:
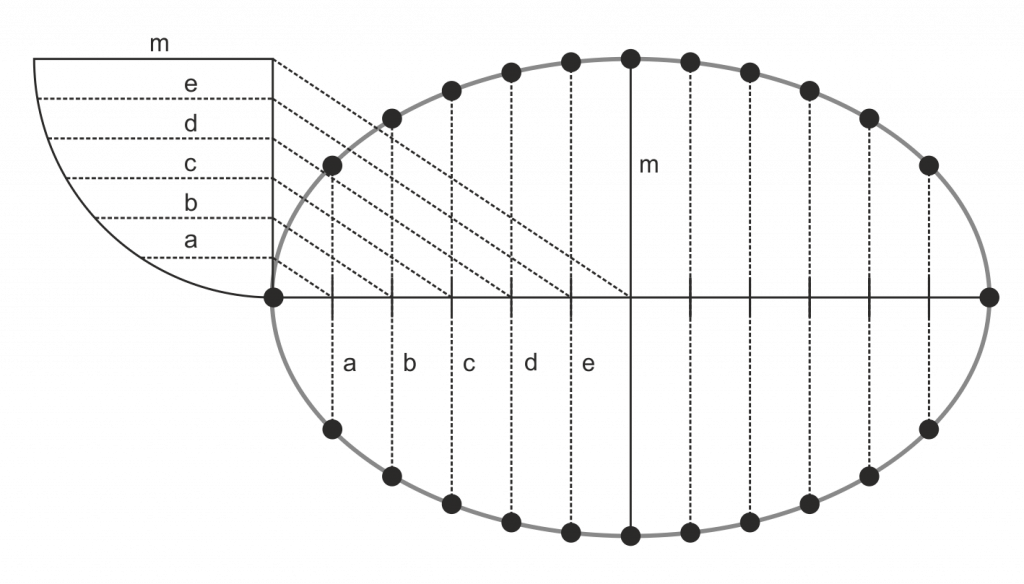
Trazado de la Elipse por proporcionalidad de ejes
- Dividimos el semieje mayor en varias partes (6 en la figura)
- Dibujamos un sector circular de 90º y radio igual al semieje menor (, adosado al extremo del eje mayor (para facilitar el trazado) y dividimos su radio en igual número de partes
- Trazamos perpendiculares al radio dividido y obtenemos las alturas proporcionales en la dirección del eje menor (segmentos a, b, c, d y e)
- Trasladamos esas alturas como segmentos perpendiculares al eje mayos, dando los puntos de la elipse (los de la parte derecha también se pueden hacer por simetría)
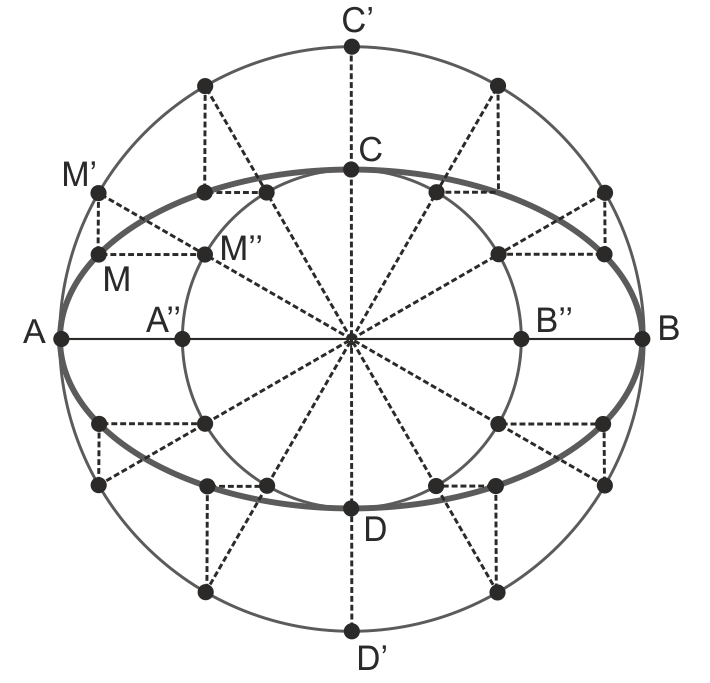
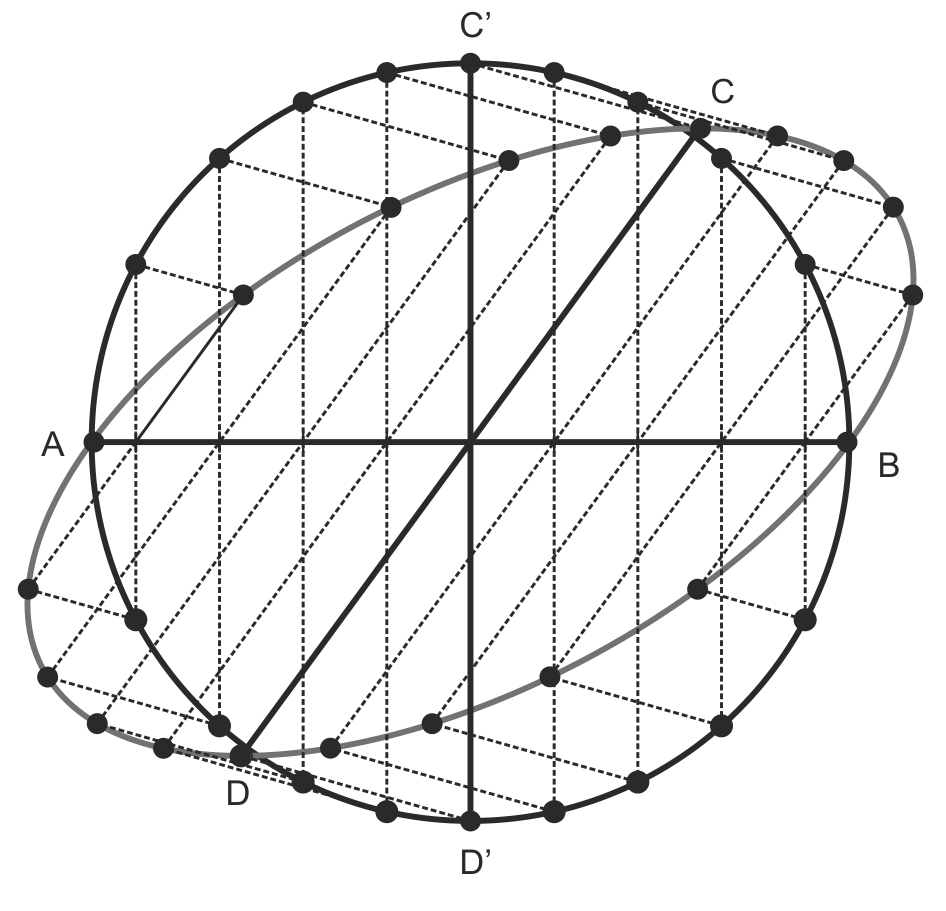
Trazado de la Elipse por Afinidad a partir de los ejes
Partiendo de los ejes:
- Trazamos las circunferencia principal y la que tiene como diámetro el eje menor.
- Una afinidad vertical de eje AB y dirección C-C’ convierte a la circunferencia mayor en la elipse, y una afinidad horizontal de eje CD y dirección A-A’’ convierte a la circunferencia menor en la misma elipse.
- Hacemos divisiones iguales en ambas circunferencias.
- Tomamos un punto M’ que se convierte en punto de la elipse por la afinidad vertical. El equivalente en la circunferencia menor, M’’, lo hace por afinidad horizontal. El punto M, corte de las dos direcciones, pertenece a la elipse.
- Se repite para todas las divisiones tomadas, obteniendo diferentes puntos de la curva.
Trazado de la Elipse por Afinidad a partir de dos diámetros conjugados AB y CD
- Dibujamos una circunferencia con diámetro igual a uno de los diámetros (en la figura, AB)
- Definimos una afinidad que convierta la circunferencia en la elipse. El punto C’ de la circunferencia se convertirá en el C de la elipse (extremo del otro diámetro conjugado)
- Dividimos el diámetro AB en varias partes y levantamos verticales para dar varios puntos en la circunferencia
- Aplicamos la afinidad a cada uno de esos puntos. Como las afines de dos rectas paralelas también son paralelas, la dirección del diámetro DC cortada con la dirección de afinidad dará los diferentes puntos de la elipse.
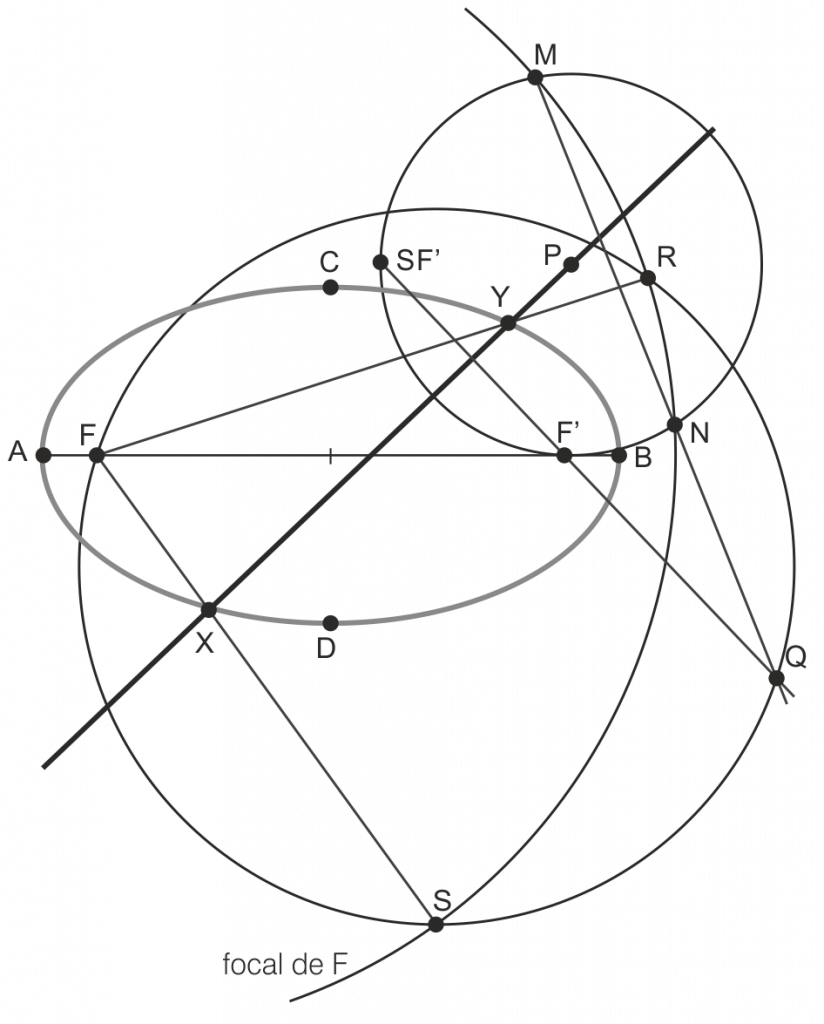
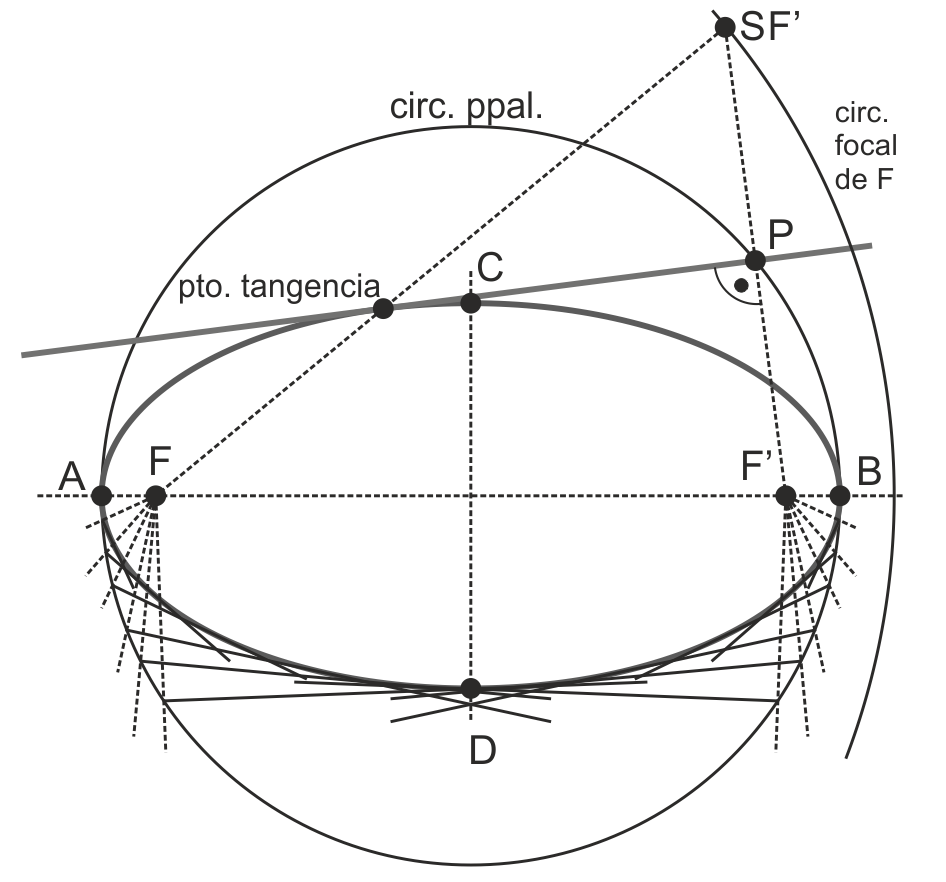
Trazado de la Elipse por tangentes envolventes
- Sabemos que el simétrico de un foco respecto a una tangente está en la circunferencia focal del otro foco, y que el punto medio está en la circunferencia principal.
- Dibujamos la circunferencia principal. Elegimos un punto P de ella y trazamos el simétrico del foco F’ (SF’, perteneciente a la focal de F). La perpendicular a F-SF’ por P será una tangente de la elipse. El punto de tangencia está en la recta F-SF’.
- Si trazamos rectas que parten de los focos y hallamos sus perpendiculares donde cortan a la circunferencia principal, estamos construyendo tangentes envolventes de la elipse (en la figura, se ha hecho en la mitad inferior de la elipse).
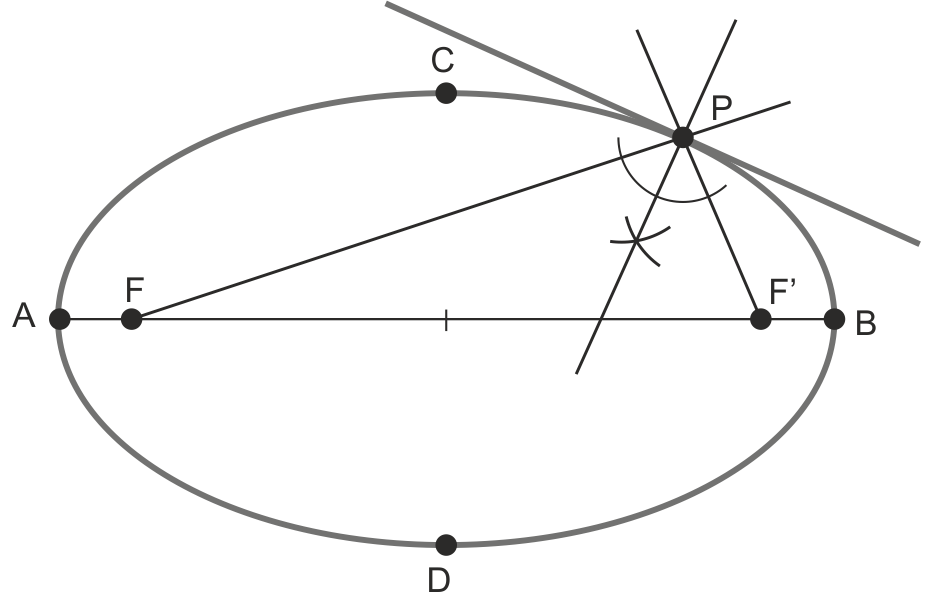
Tangente y normal a una Elipse por un punto propio P
- Trazamos sus radiovectores y encontramos la bisectriz de ambos.
- Esta bisectriz es la normal a la elipse en P, así que su perpendicular por P será la tangente buscada.
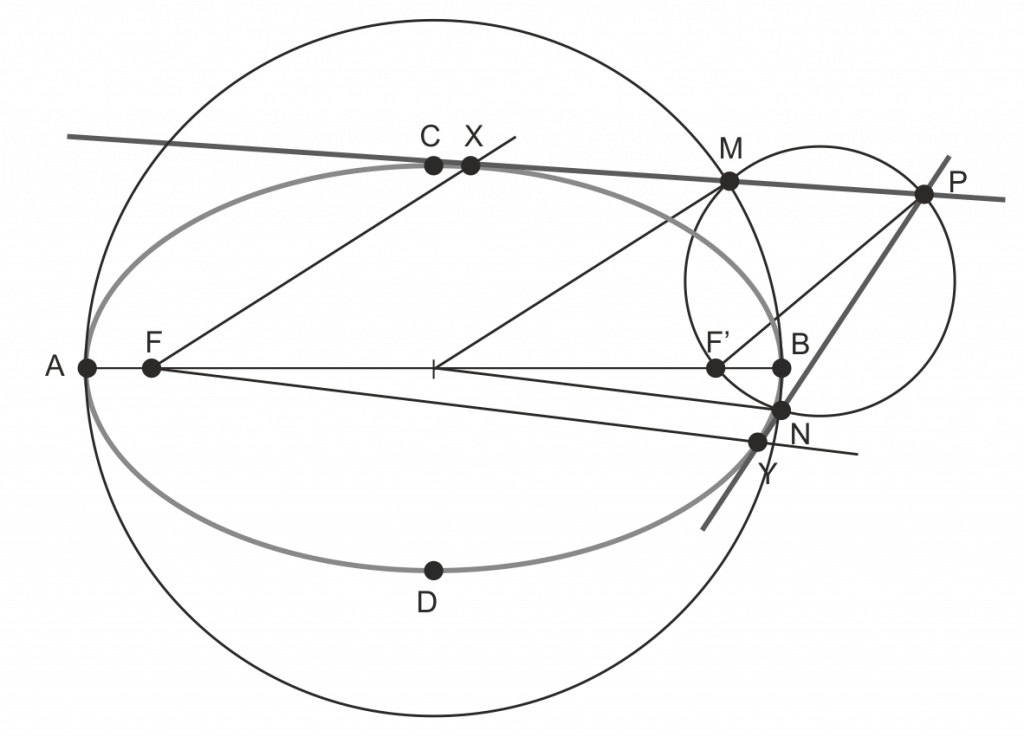
Tangentes a una Elipse por un punto exterior (por la circunferencia principal)
Para encontrar las tangentes a la elipse por un punto exterior P:
- Trazamos la circunferencia principal
- Elegimos un foco (en el ejemplo, F’, por ser mas cercano a P) y trazamos la circunferencia de diámetro F’P, que corta a la circunferencia principal en M y N
- PM y PN son las tangentes buscadas
- Para encontrar los puntos de tangencia, unimos el centro de la elipse con N y M y trazamos paralelas a estas dos rectas por el otro foco. Donde corten estas últimas a las tangentes están los puntos de tangencia (X e Y)
Tangentes a una Elipse por un punto exterior (por las circunferencias focales)
Para encontrar las tangentes a la elipse por un punto exterior P:
- Trazamos la circunferencia focal del foco F
- Con centro en F y radio PF’ trazamos un arco que costará a la focal anterior en M y N
- Las mediatrices de los segmentos F’M y F’N son las tangentes buscadas
- Para encontrar los puntos de tangencia, trazamos FM y FN, que se cortan con las tangentes en los puntos de tangencia, X e Y

Tangentes a una Elipse paralelas a una dirección (por la circunferencia principal)
Para encontrar las tangentes a una elipse paralelas a la dirección dada por la recta r:
- Trazamos la circunferencia principal de la elipse
- Dibujamos la perpendicular a la recta r por un foco (F’ en la figura), dando los puntos M y N en la circunferencia principal. Las paralelas a r por M y N son las tangentes buscadas
Para encontrar los puntos de tangencia, trazamos las rectas que unen el centro de la elipse con M y N y dibujamos sus paralelas por el otro foco, que cortan a la tangente en los puntos X e Y
Tangentes a una Elipse paralelas a una dirección (por las circunferencias focales)
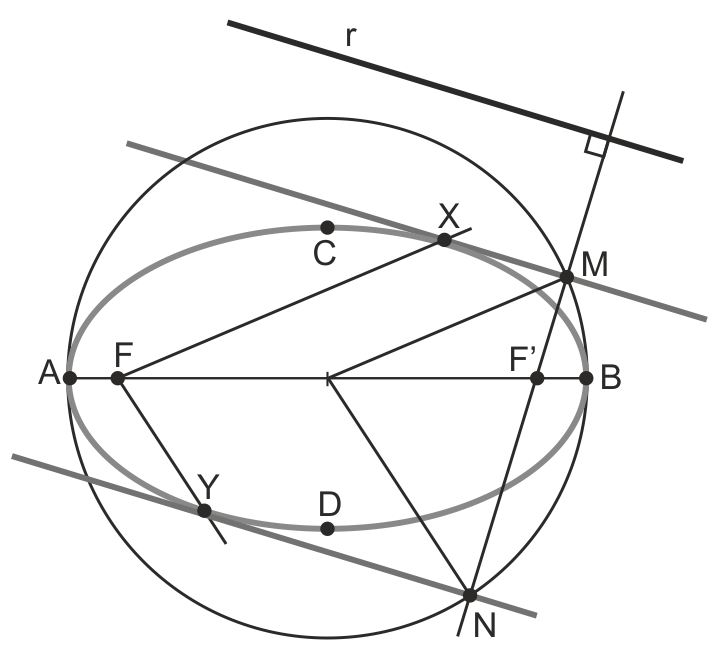
Para encontrar las tangentes a una elipse paralelas a la dirección dada por la recta r:
- Trazamos la focal del foco F
- Por el otro foco se traza la perpendicular a la recta, que corta ala focal anterior en M y N
- Las mediatrices de F’M y F’N son las tangentes buscadas
- Para encontrar los puntos de tangencia, basta trazar las rectas FM y FN, que cortan a las tangentes en los puntos buscados, X e Y

Intersección entre una Elipse y una recta secante
Para determinar la intersección de una elipse con una recta secante r:
- Trazamos la focal de F
- Encontramos el simétrico del otro foco (F’) con respecto a la recta r (SF’)
- Elegimos un punto P cualquiera sobre la recta tal que al trazar una circunferencia de radio PF’ corte a la focal de F en M y N
- Prolongamos M-N y F-SF’ hasta que se cortan en Q
- Dibujamos la circunferencia de diámetro QF, que cortará a la focal en los puntos R y S
- Al unir F con R y S obtenemos sobre r los puntos de corte buscados, X e Y