Tipos de plataformas

En las obras lineales como carreteras y caminos, las plataformas suelen estar compuestas por diferentes segmentos, que serán, básicamente:

• Rectos
• Arcos de circunferencia
• Curvas de enlace entre segmentos rectos y/o arcos (se verán en detalle en un capítulo posterior)

En las plataformas de contornos rectos (por ejemplo, los tramos rectos de las carreteras), sean horizontales o tengan pendiente, los taludes de desmonte y terraplén serán planos.

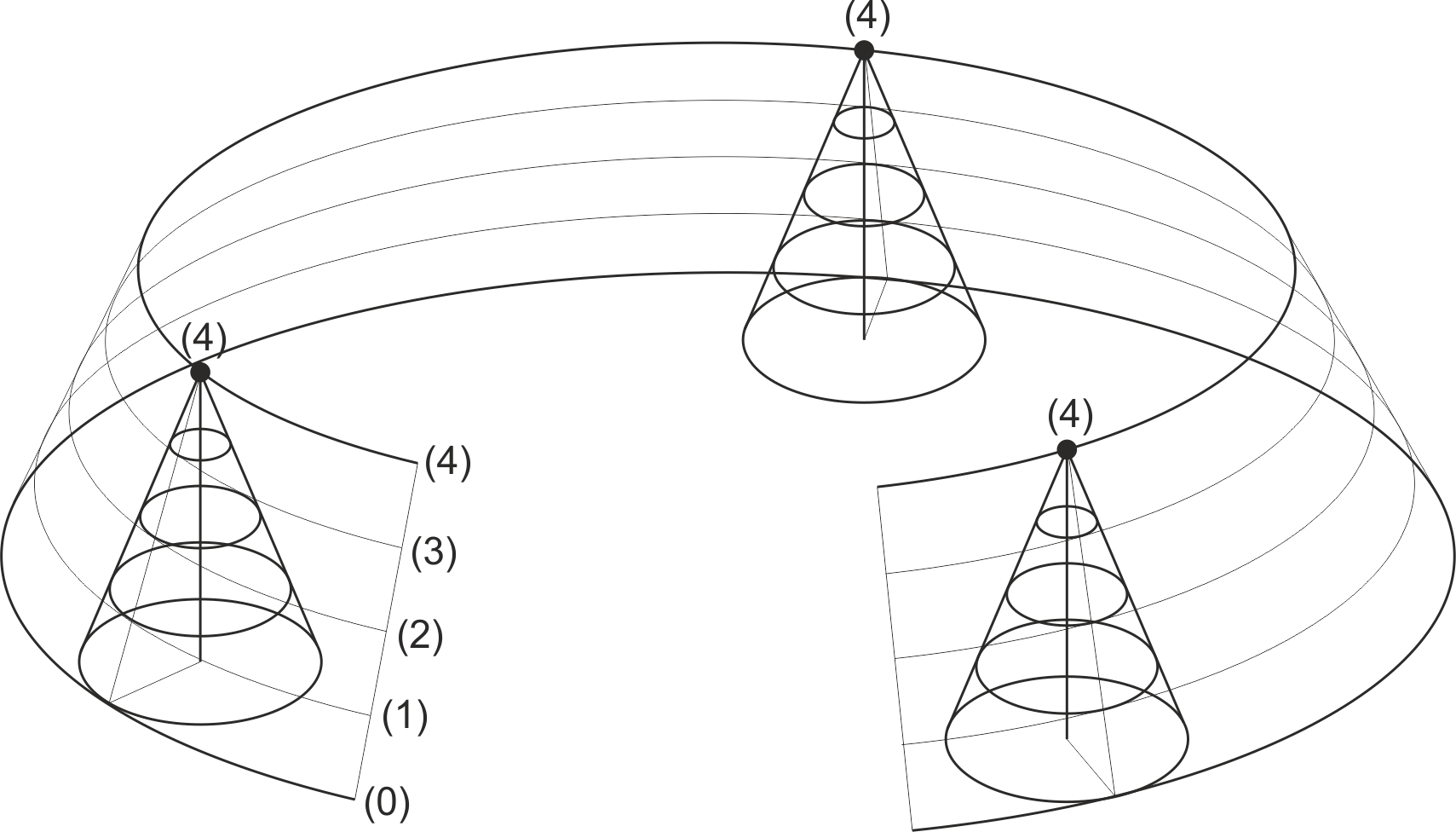
En las plataformas con contornos circulares (arcos) horizontales, los desmontes y terraplenes serán superficies cónicas.

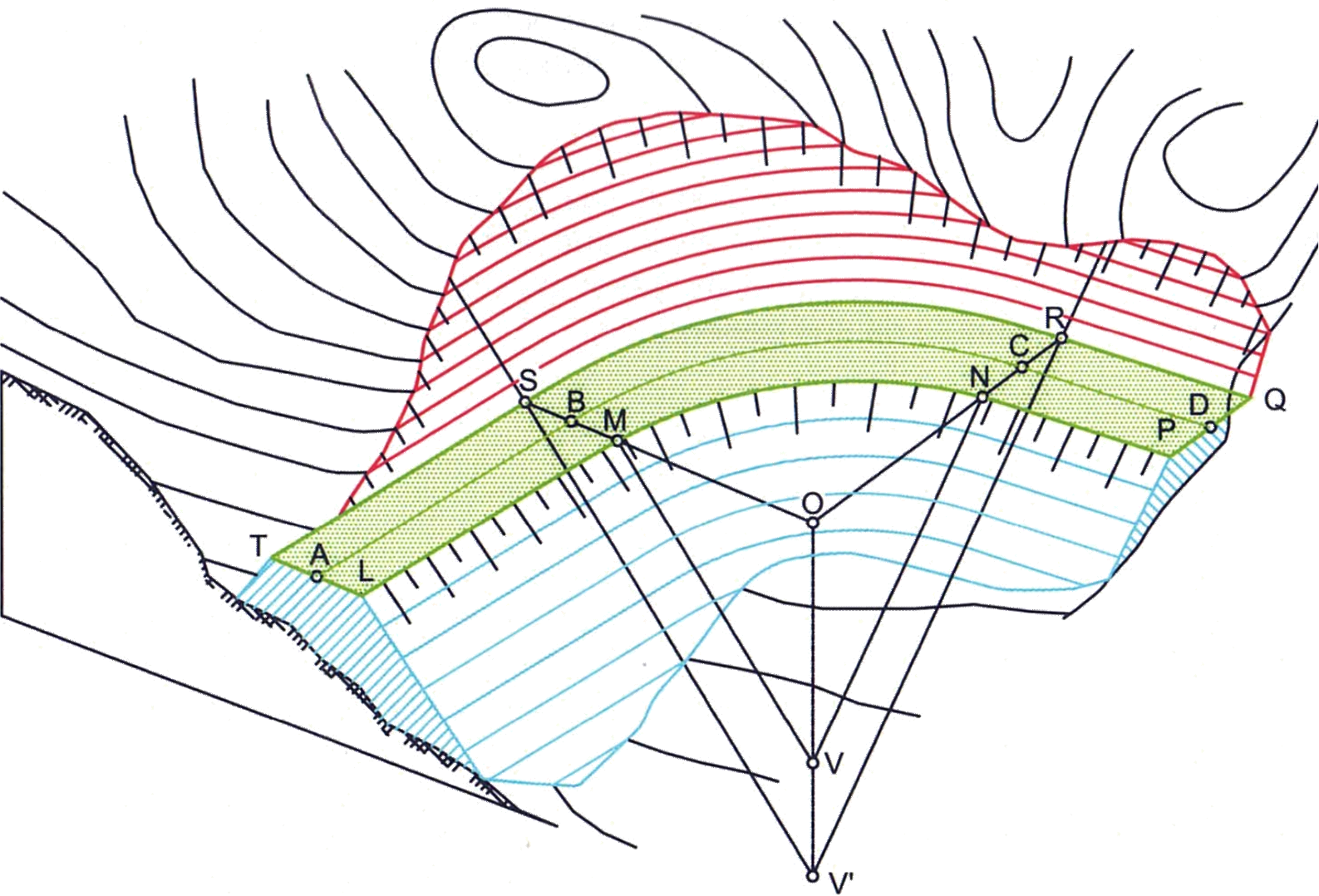
Como se verá más adelante, los taludes de desmonte y terraplén de curvas con pendiente no nula son superficies regladas desarrollables denominadas helicoides.

Superficies de talud

Las superficies de talud son aquellas que presentan en cualquiera de sus puntos una máxima pendiente constante en relación con un plano de referencia. Esto quiere decir que un plano tangente en cualquier punto de ella forma un ángulo fijo con el plano de referencia (normalmente, el plano horizontal).

Las líneas de máxima pendiente en una superficie de talud son rectas, y los planos tangentes contienen a su vez a estas rectas de pendiente. Es por esto que las superficies son desarrollables.

Puede decirse que estas superficies son envolventes de diferentes planos que forman un ángulo fijo con el de referencia, o lo que es lo mismo, están engendradas por un plano que formando un ángulo fijo con el de referencia, que se mueve permaneciendo tangente a una curva llamada directriz.

En una superficie de talud, las líneas de nivel son paralelas y equidistantes.

Desde el punto de vista de los conos de talud, las superficies de talud son las envolventes a dichos conos cuando estos toman diferentes posiciones, con el vértice en un punto de la curva directriz.

Taludes planos

Si consideramos que el punto de vertido se desplaza de forma lineal, y se van formando conos de vertido de diferente altura, las dos superficies envolventes de esos conos son dos planos que tienen el mismo talud de los conos, los denominados planos de talud del terreno.

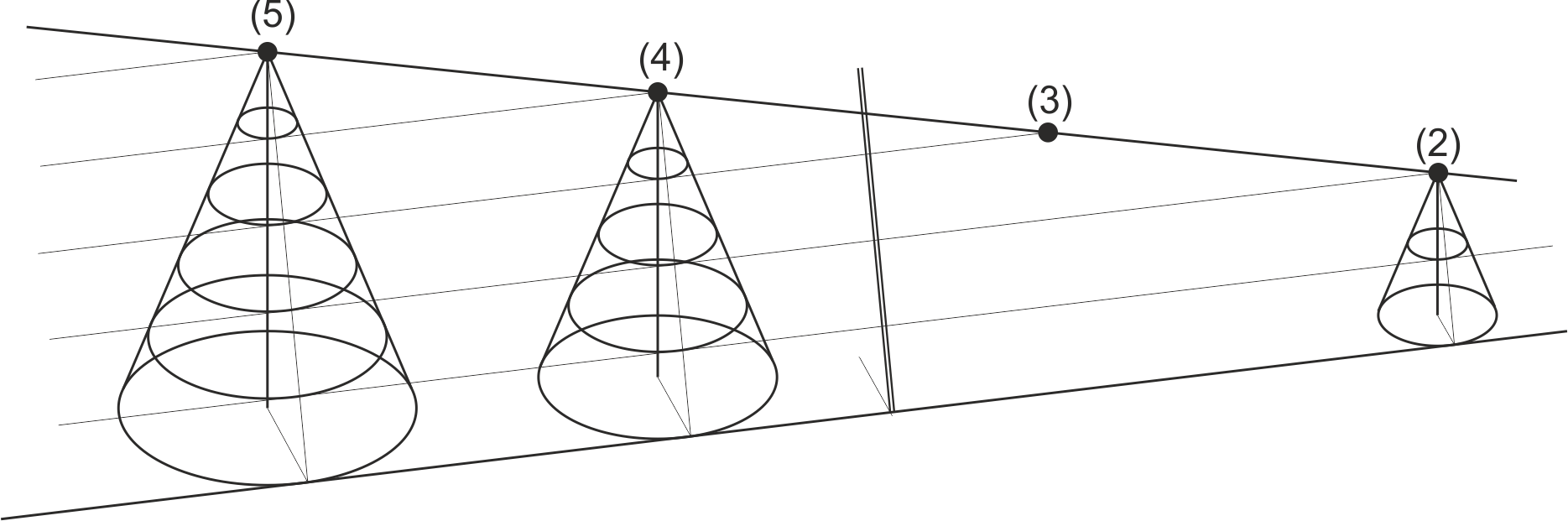
Las líneas de nivel de esos planos son tangentes a los círculos de nivel de los conos (en la figura se representa únicamente uno de los dos planos), y las líneas de máxima pendiente de esos planos son paralelas a las generatrices de tangencia en los conos.

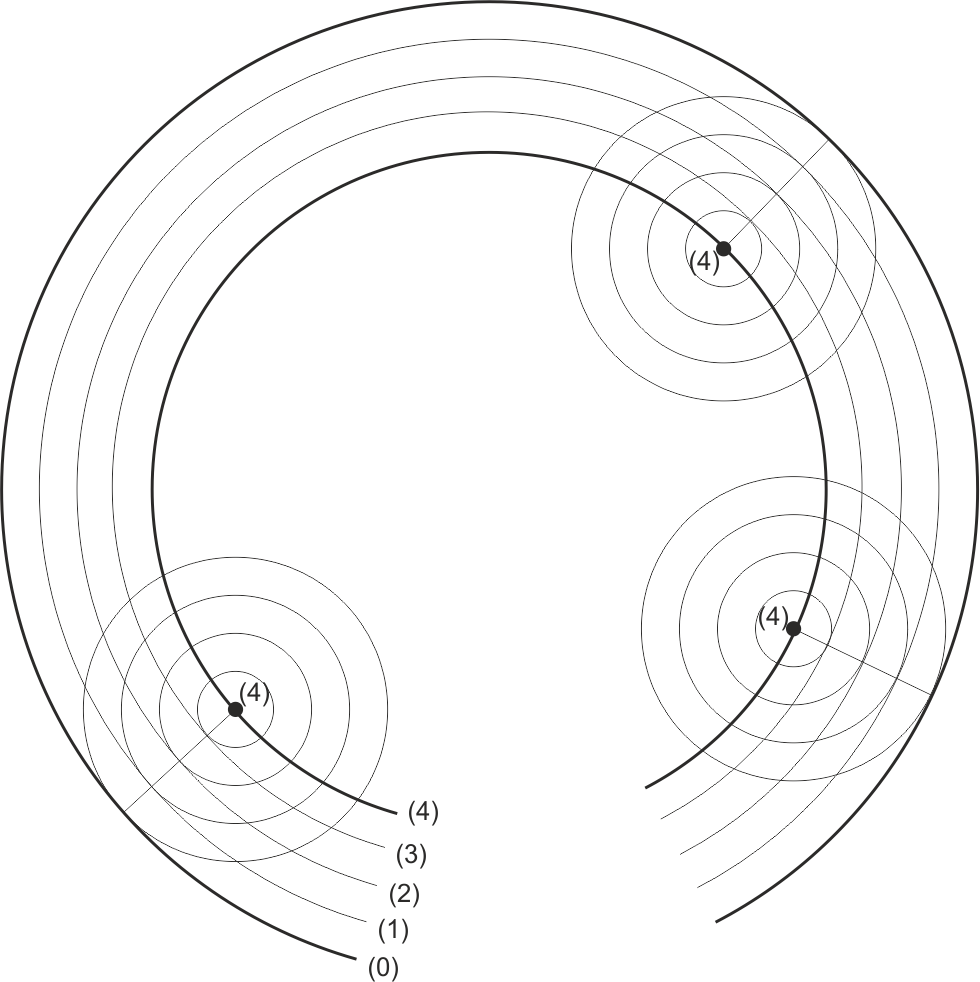
Si lo vemos en sistema acotado, las líneas de nivel aparecen como tangentes comunes a los conos de talud, a una distancia entre ellas igual al módulo o talud del terreno.

Dependiendo de la pendiente de la recta que une los vértices el sistema tendrá una solución (si la recta tiene la misma pendiente que el cono), dos (como en el ejemplo) o ninguna solución (si la pendiente de la recta es mayor que la de los conos, en cuyo caso es imposible que la recta pertenezca a los planos).

Taludes curvos

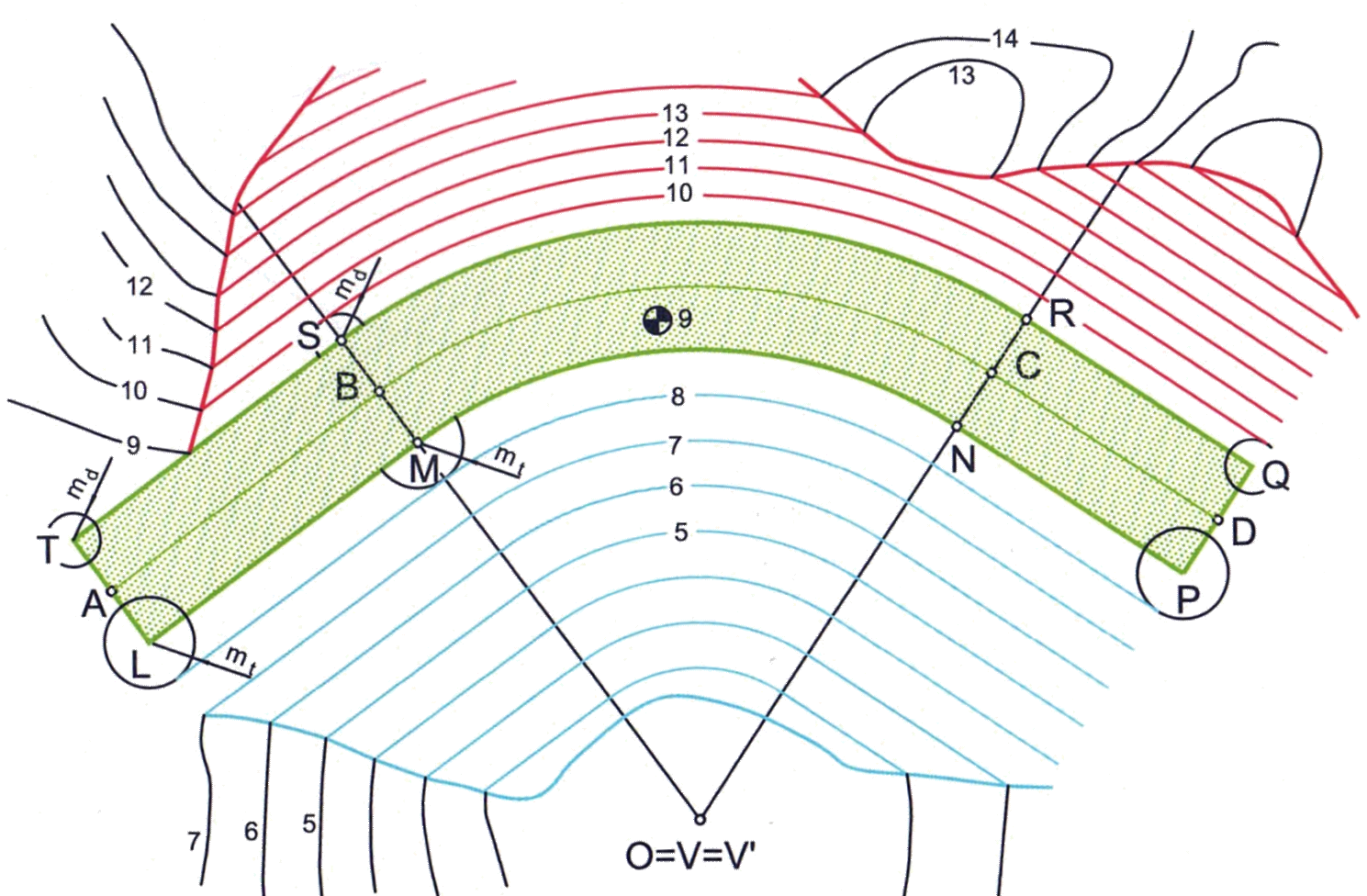
Si el desplazamiento del punto de vertido (vértices de los conos) no es a lo largo de una recta, sino que sigue una curva continua en el espacio, los conos generan una superficie envolvente (una superficie reglada y desarrollable). También es posible que haya una, dos o ninguna solución, dependiendo de la pendiente que tenga la curva. En todos los puntos, la superficie tiene la misma pendiente. En la figura se ha representado solo una de las dos soluciones.

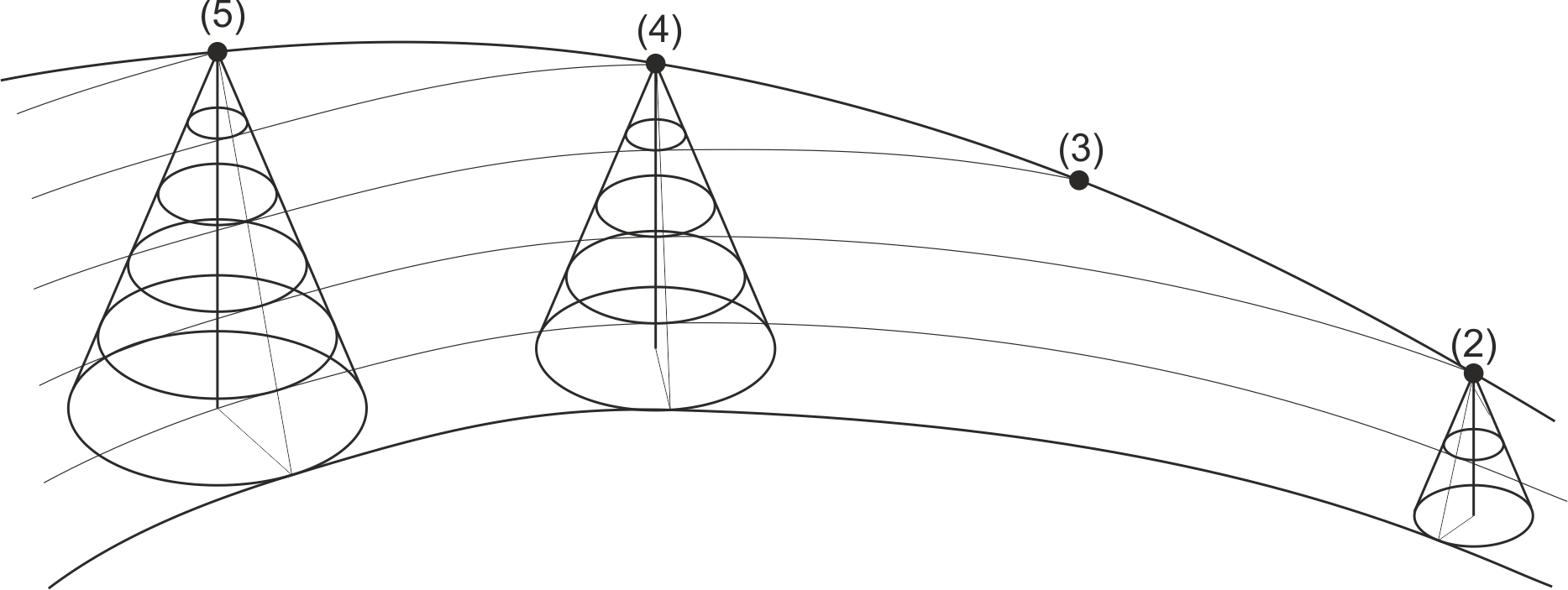
Igual que en el caso anterior, si las vemos en sistema acotado, las líneas de nivel aparecen como tangentes comunes a los conos de talud, a una distancia entre ellas igual al módulo o talud del terreno.

El método de los conos de talud es aplicable en prácticamente cualquier caso de plataforma, horizontal o no. Conociendo la pendiente de talud, una vez determinadas las líneas de paso, basta con dibujar conos de talud de desmonte o terraplén en varios puntos del contorno y trazar las envolventes a las circunferencias de nivel directrices de dichos conos.

Taludes cónicos

Un caso especial es cuando la curva descrita por los vértices de los conos es un arco de circunferencia horizontal. En este caso, la superficie envolvente generada es a su vez un cono de revolución. Las líneas de nivel son circunferencias tangentes a las circunferencias directrices de los conos.