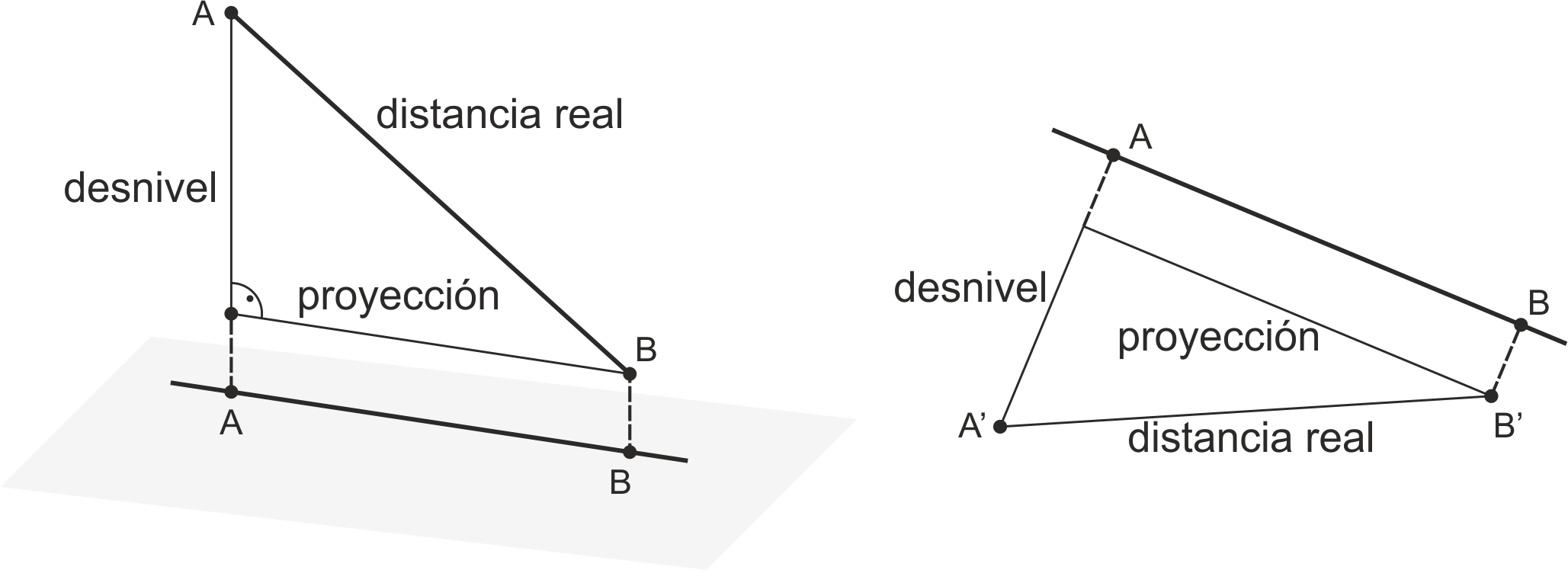
Distancia entre dos puntos (longitud de un segmento)

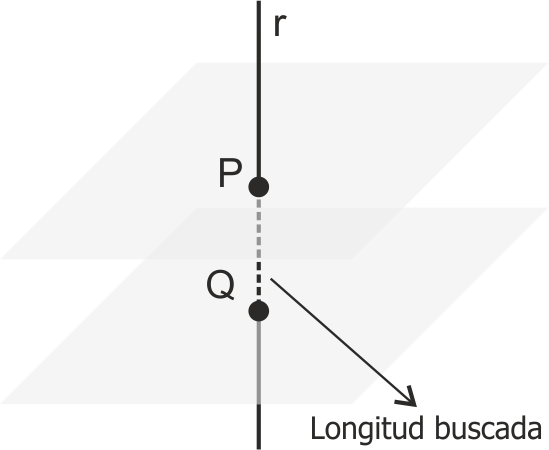
Para medir un segmento (o realizar el problema inverso, llevar una longitud dada a una recta) basta con abatir la recta que lo contiene. La recta abatida la vemos en verdadera magnitud, así que sobre ella podemos llevar y tomar las distancias en escala real.

Si consideramos un triángulo rectángulo en el cual un cateto es el segmento proyección y el otro es el desnivel, la hipotenusa representa la distancia buscada.

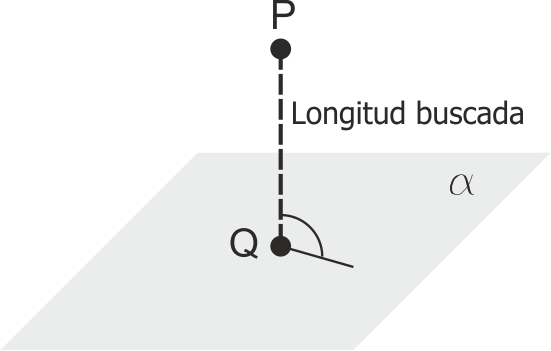
Distancia entre un punto y un plano

La distancia desde un punto a un plano es la longitud del segmento que forma con dicho punto con el pie de la perpendicular trazada por él al plano.

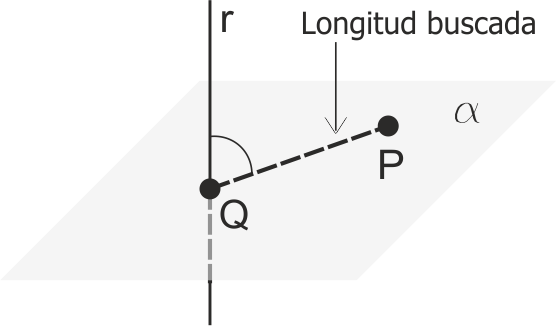
Distancia entre un punto y una recta

La distancia desde un punto a una recta es la longitud del segmento perpendicular a la recta trazado desde el punto. Para encontrarlo, buscamos el plano que contiene al punto y es perpendicular a la recta. La intersección de ese plano con la recta es el segundo punto del segmento buscado.

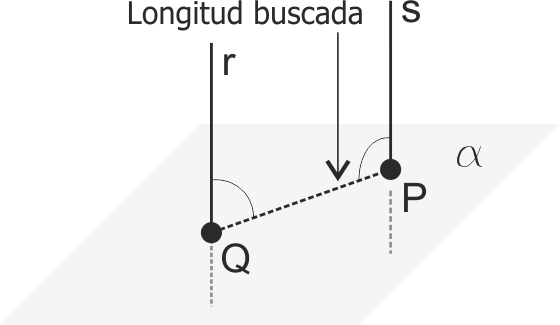
Distancia entre dos rectas paralelas

La distancia entre dos rectas paralelas es la de cualquier segmento perpendicular a ambas. Para encontrarlo, tomamos un plano cualquiera que sea perpendicular a las dos, y las intersecciones con ambas pro-porcionan ese segmento.

Distancia entre dos planos paralelos

La distancia entre dos planos paralelos es la longitud de un segmento perpendicular a ambos. Basta tomar una recta perpendicular cualquiera y encontrar las intersecciones con los planos.

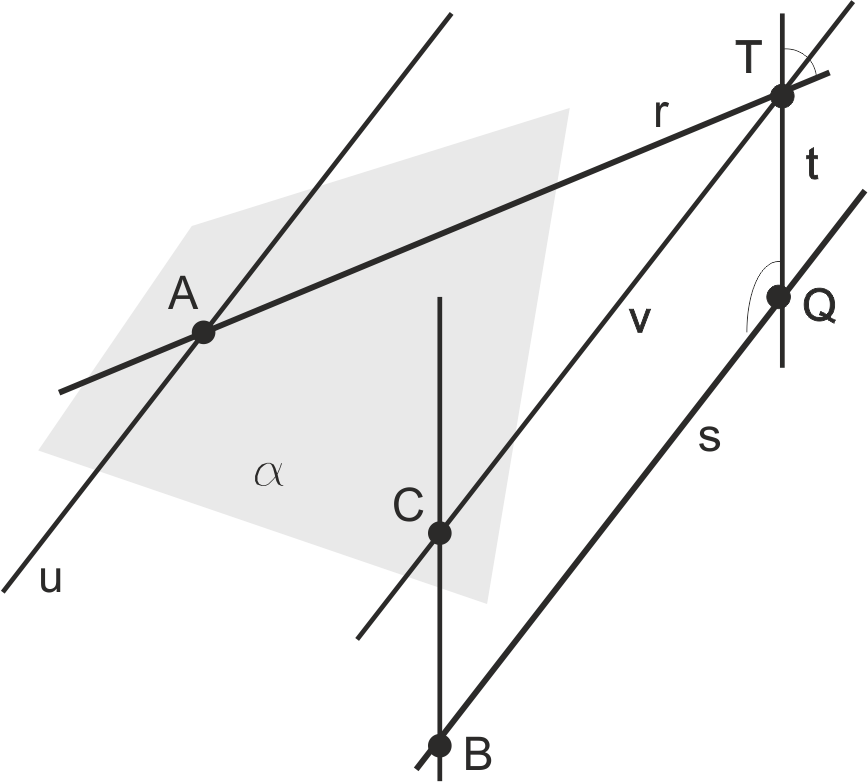
Mínima distancia entre dos rectas que se cruzan

La mínima distancia entre dos rectas (r, s) que se cruzan es la longitud de un segmento perpendicular a ambas. Para encontrarlo, trazamos un plano (a) que contenga a una recta (r) y sea paralelo a la otra. La distancia entre cualquier punto (B) de esta última recta y el plano es la solución buscada (BC en la figura). Si además queremos encontrar su ubicación, por el pie de esta perpendicular trazada (C) trazamos una paralela a la segunda recta, que se corta con la primera en uno de los extremos del segmento (T). TQ es el segmento buscado.

Abatimiento de una recta

Ya hemos abatido un segmento en muchas de las figuras anteriores. Basta con llevar sobre perpendiculares a la proyección distancias equivalentes a las cotas de los puntos a abatir.

Abatimiento y desabatimiento de un plano y de figuras planas

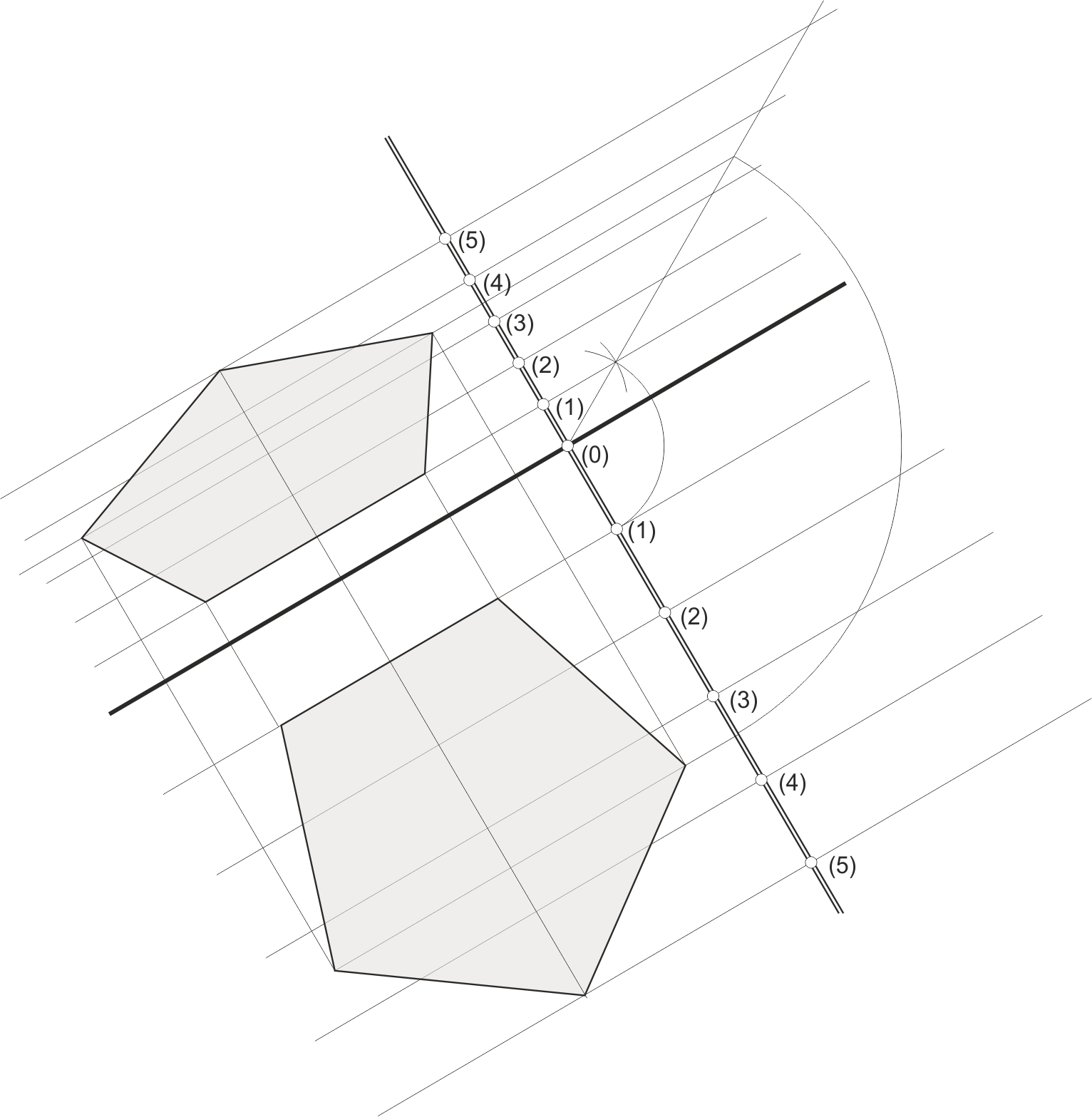
En Acotado, entendemos por abatir un plano el girarlo alrededor de su traza (o de una horizontal del plano elegida como charnela) hasta hacerlo horizontal. Si se abate alrededor de la traza, el plano de abatimiento es el plano horizontal de cota 0. De esta forma, cualquier figura plana contenida en él la podremos apreciar en verdadera proporción y magnitud en el plano abatido.

Por comodidad, el abatimiento lo realizamos hacia el lado que forma el mayor ángulo con el plano horizontal, de forma que al trazar las figuras abatidas no se mezclen con las proyecciones de las mismas en el plano original.

Desabatir un plano abatido (y una figura contenida en él) consiste en trasladar los puntos de la figura trazada en él (en verdadera magnitud) al plano original.

En este ejemplo, hemos abatido un plano para colocar en él un pentágono regular, que a su vez hemos desabatido sobre el plano original. Todo lo hemos hecho con ayuda de una lmp que hemos usado para encontrar la distancia real entre las horizontales del plano. Nótese que el desabatimiento de los vértices del pentágono que tienen cota 1 y 5 es inmediato, ya que basta trasladarlos en las líneas horizontales en ambos planos, el original y el abatido. Para encontrar los otros dos, hemos trazado una horizontal auxiliar del plano abatido, que hemos trasladado al plano original.

Proyecciones de una circunferencia

Sabemos que la proyección cilíndrica de una circunferencia es una elipse, y que dos diámetros perpendiculares se proyectan como dos diámetros conjugados de esa elipse. Es fácil deducir que, si dibujamos la circunferencia en el plano abatido y tomamos un diámetro paralelo a las horizontales del plano y otro perpendicular, obtendremos los ejes de la elipse en el plano original.

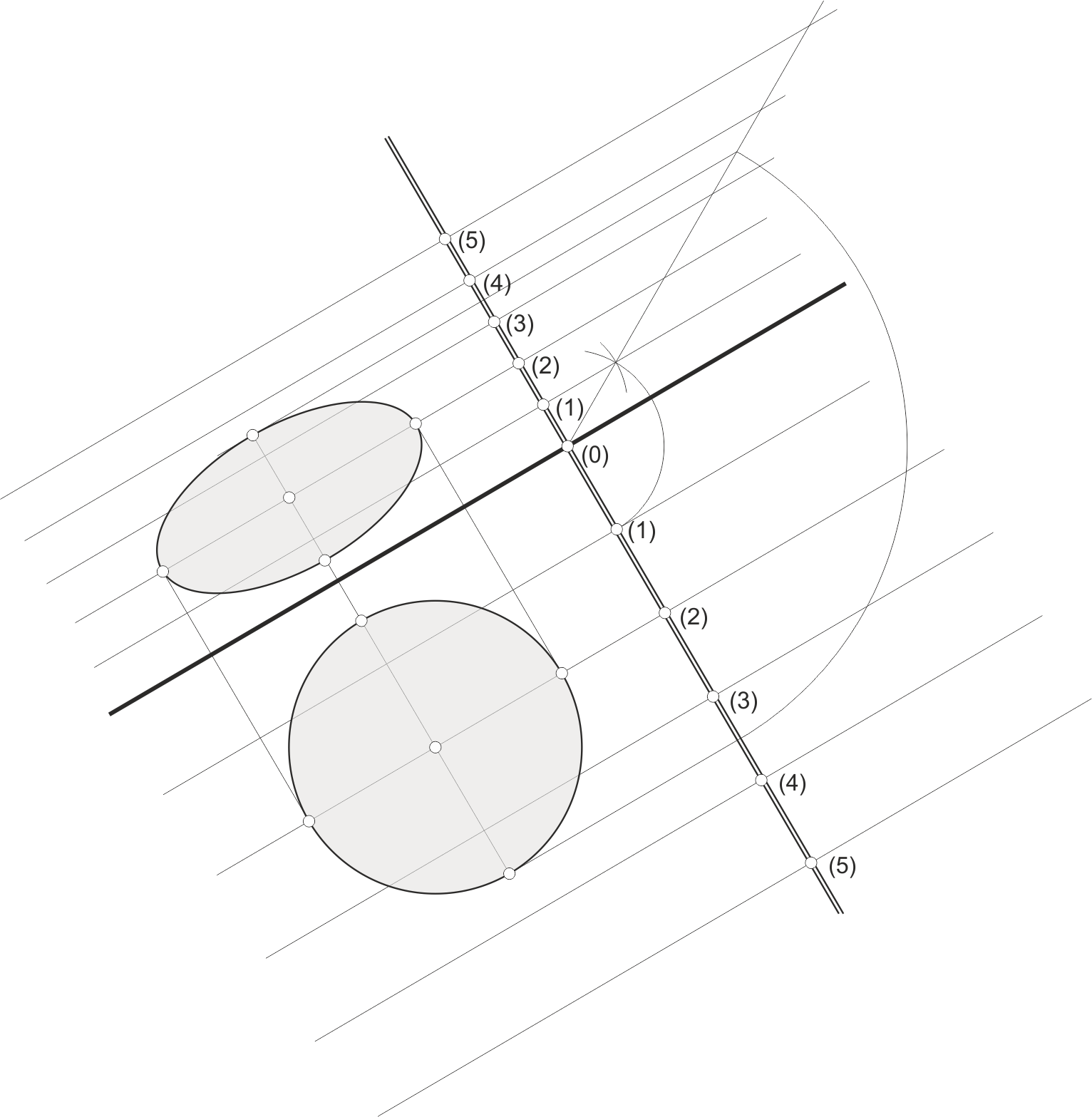
Podemos comprobar que, tal y como ocurría en el Sistema Diédrico, existe una relación de afinidad entre la figura original (proyección) y la figura abatida, en la cual el eje es la charnela y la dirección es la perpendicular a ella.

Ángulo entre dos rectas

Para encontrar el verdadero ángulo entre dos rectas que se cortan, basta con abatir el plano que las contiene a ambas. En el plano abatido las veremos en verdadera proporción y, por tanto, también tendremos el ángulo que forman en verdadera magnitud.