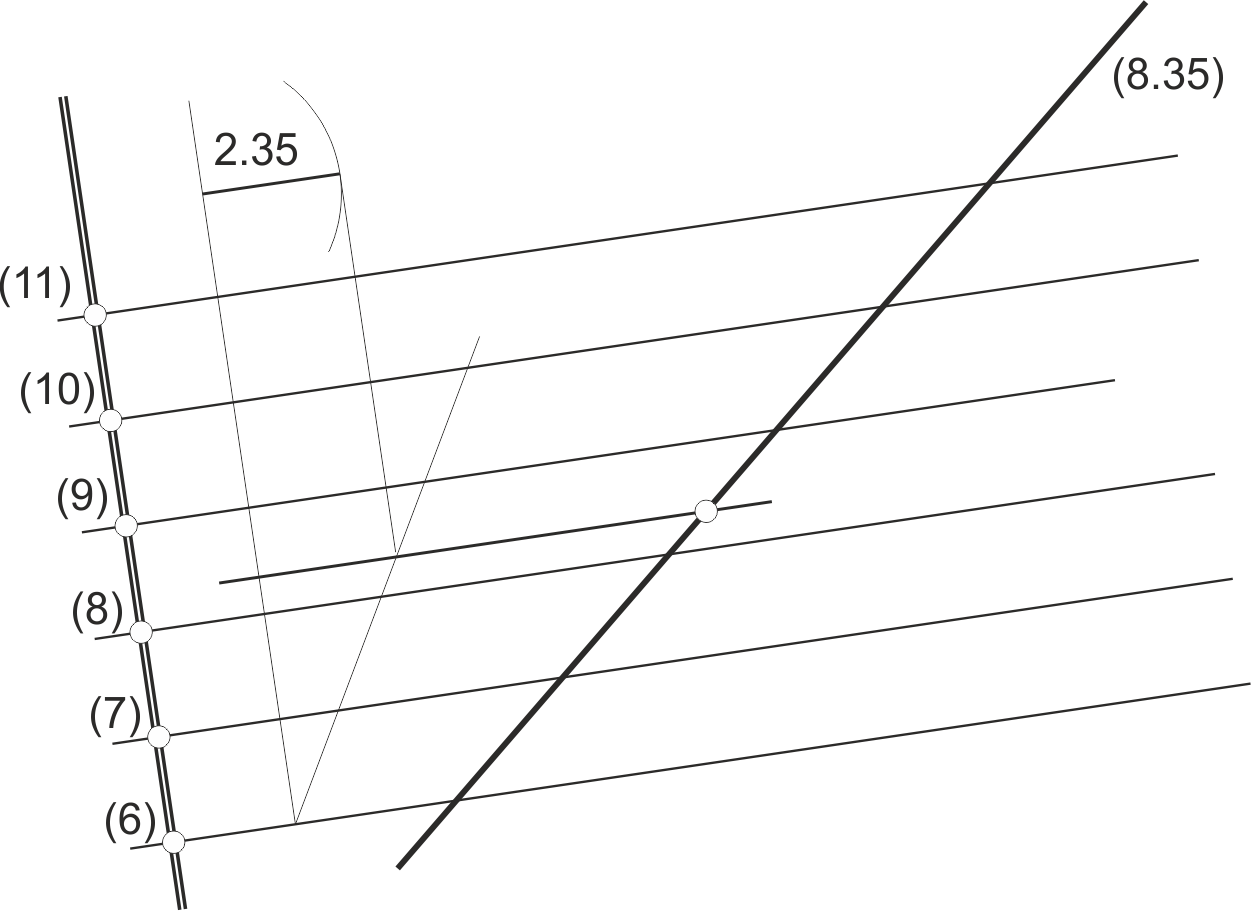
Intersección entre dos rectas

Para que dos rectas se corten, el punto de corte de sus proyecciones debe tener la misma cota para ambas rectas. Si no es así, las rectas se cruzan en el espacio (ver capítulo anterior).

Intersección entre dos planos

Para encontrar la recta intersección entre dos planos, basta unir los puntos donde se cortan dos pares de horizontales de igual cota en ambos planos.

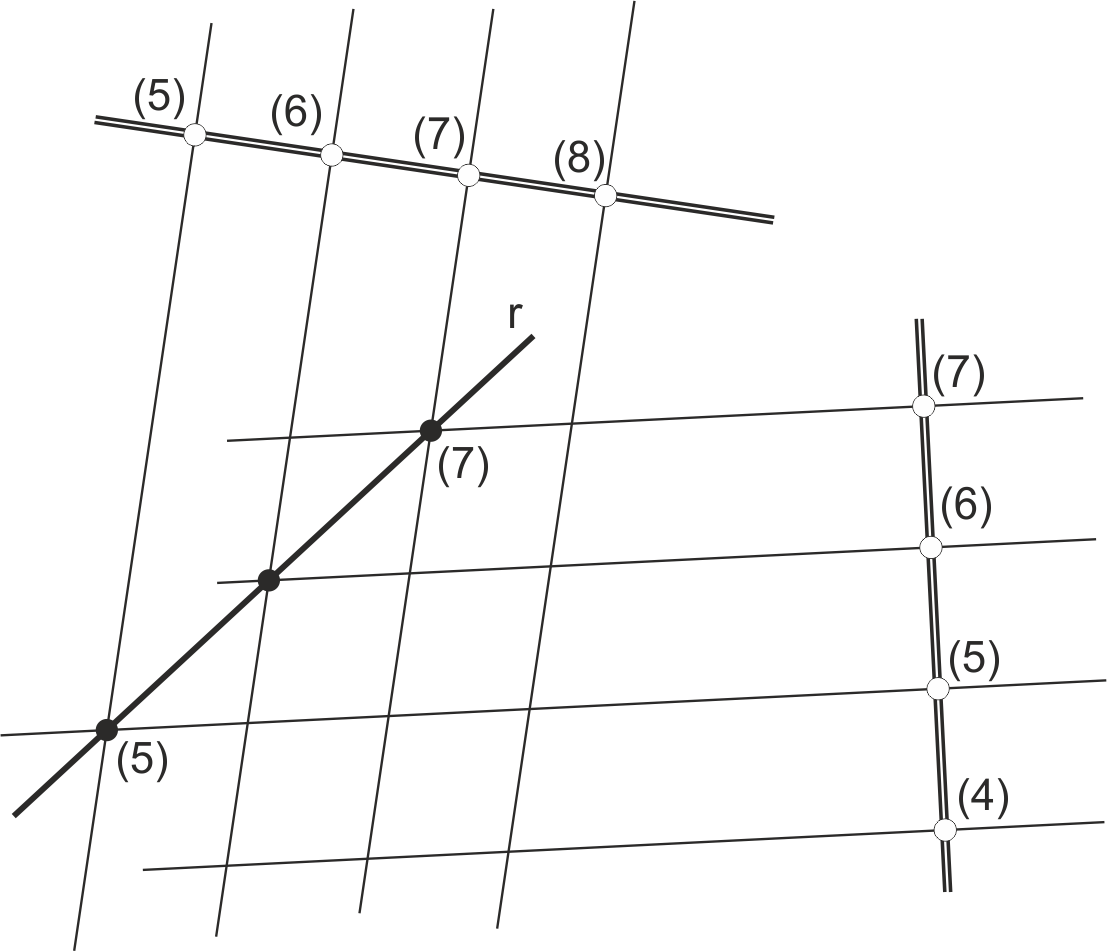
Si los planos tienen trazas paralelas el resultado es la horizontal común a ambos planos, que se encuentra abatiendo dos rectas de máxima pendiente del plano elegidas en una perpendicular común a las trazas (usando la misma cota como referencia). En la figura, esas rectas son r y s. Si medimos la distancia x de la figura podemos obtener la cota de la recta intersección (sumando 5, que es la cota de referencia).

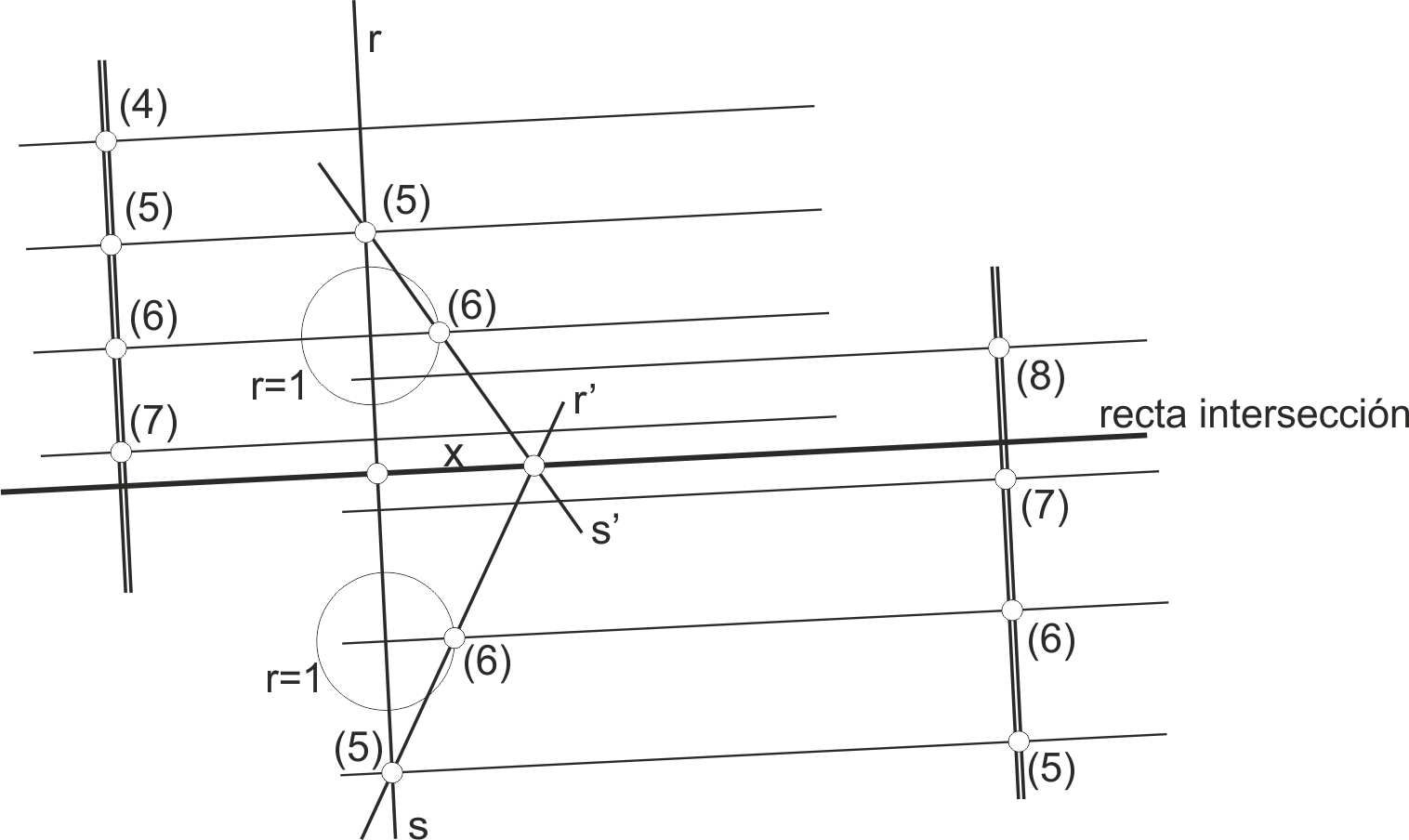
Intersección entre recta y plano

La intersección entre una recta y un plano es un punto, siempre que la recta no sea paralela al plano o pertenezca a él.

Para encontrarlo, trazamos un plano cualquiera que contenga a la recta, que se cortará con el otro plano a su vez en otra recta. La intersección de ambas rectas es la solución buscada. Por comodidad, este plano auxiliar suele tomarse como el plano vertical que contiene a la recta, o bien aquel cuya recta es de máxima pendiente. En ambos casos, para proceder abatimos la recta, y unimos dos puntos de igual cota con puntos del plano, para encontrar esa recta auxiliar. En el ejemplo podemos ver que el punto intersección tiene su cota entre 7 y 8, tanto para la recta como para el plano.

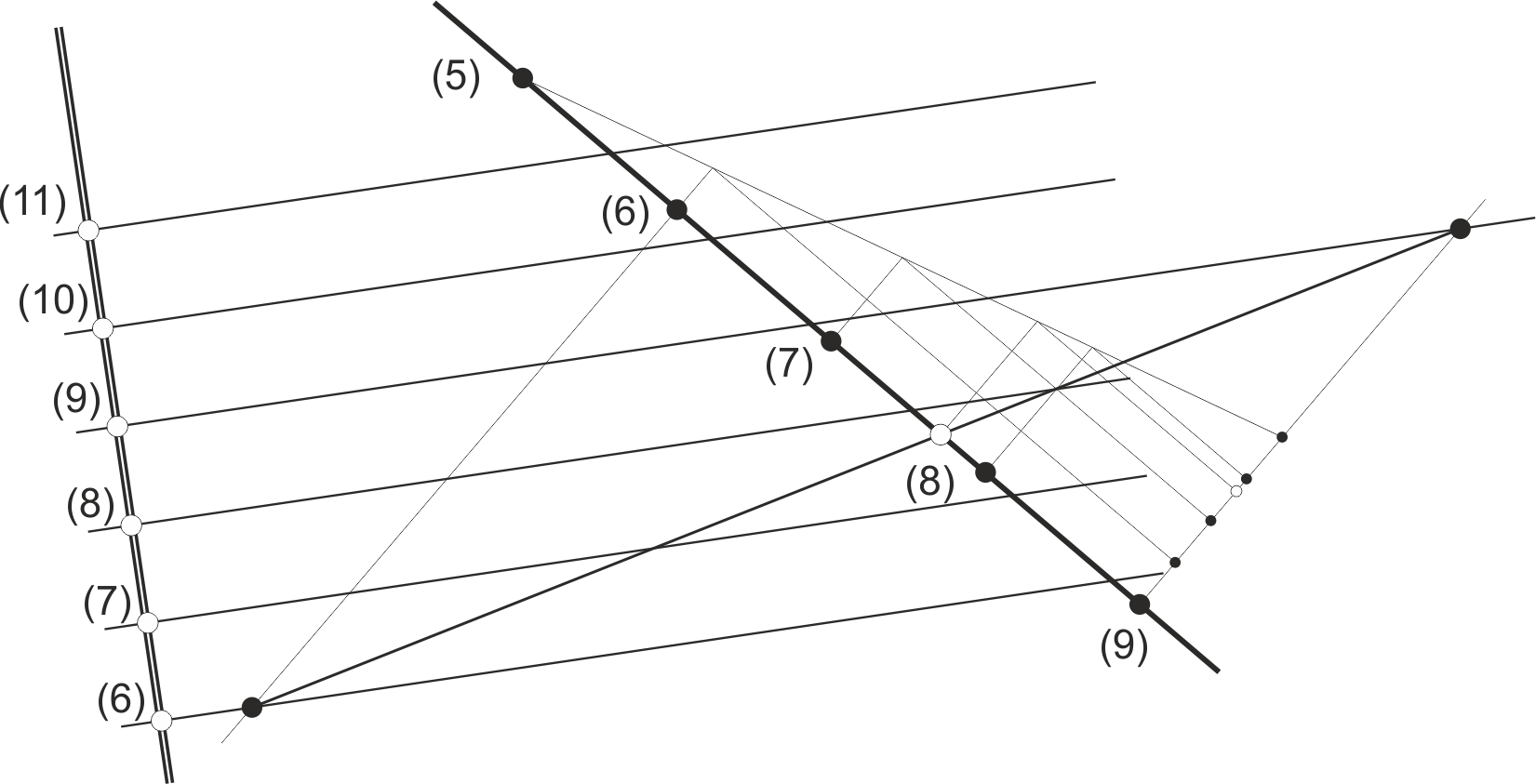
Si la recta es vertical (su proyección es un punto), basta encontrar la cota que corresponde en el plano a la proyección del punto. Para ello hemos abatido una lmp que pasa por la proyección de la recta vertical.

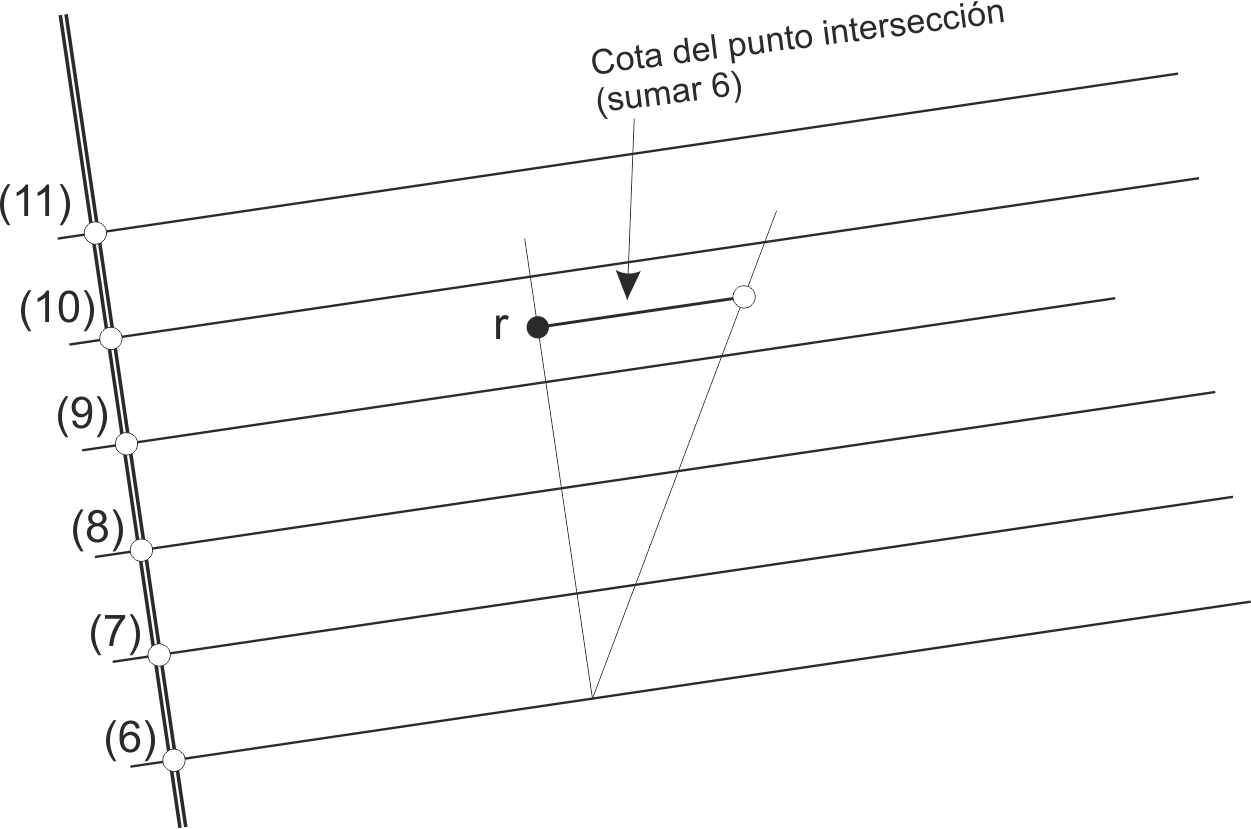
Si la recta es horizontal, el problema es inverso: basta con encontrar en el plano la horizontal cuya cota es la de la recta; ambas se intersecan en el punto de corte. Hemos abatido una lmp del plano y encontrado en ella el punto de cota deseada.