Curvatura. Conceptos

La curvatura de una curva es la desviación que esa curva sufre desde la dirección recta. Igualmente, en el espacio, la curvatura de una superficie es la desviación que sufre desde el plano. Aunque hay ciertas figuras en el plano y en el espacio cuyas curvaturas son constantes, por regla general la curvatura es diferente para cada punto de la figura.

La curvatura tiene dos aspectos cuantificables: el radio de curvatura y el centro de curvatura. Matemáticamente, el radio de curvatura es el inverso de la cuadratura en el punto. La curvatura es también la inversa del radio de curvatura.

Más allá del aspecto matemático, debemos asimilar el concepto de radio y centro de curvatura de curvas complejas a partir de los mismos elementos en figuras simples conocidas. Así, la circunferencia tiene un radio de curvatura constante (el radio de la circunferencia) y un centro de curvatura constante (el centro de la circunferencia). En una curva cualquiera, la curvatura está relacionada con el concepto de tangente, que se explica a continuación.

Recta tangente a una curva

Podemos definir la recta tangente a una curva de varias formas:

• Es una recta que une dos puntos infinitesimalmente cercanos de la misma.
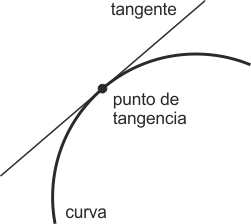
• Es una recta que toca a la curva en un único punto (punto de tangencia), y en ese punto la recta y la curva tienen ambas la misma pendiente (desde el punto de vista matemático, la pendiente de la recta tangente es el valor de la función derivada de la curva en un punto determinado).

Enlaces

Denominamos enlace a la unión mediante tangencia entre una curva y una recta o entre dos curvas. Si se trata de un enlace entre y recta y curva, la recta es la tangente a la curva en el punto de enlace. Si dos curvas son tangentes ente sí en el punto T (punto de tangencia), dicho punto T está alineado con los dos centros de curvatura de las dos curvas. Si esas curvas además son arcos de circunferencia, los centros de curvatura son los centros de estas circunferencias.

Hay que recordar también que, como extensión de lo anterior, podemos observar que la mediatriz de cualquier cuerda de una circunferencia pasa por su centro.

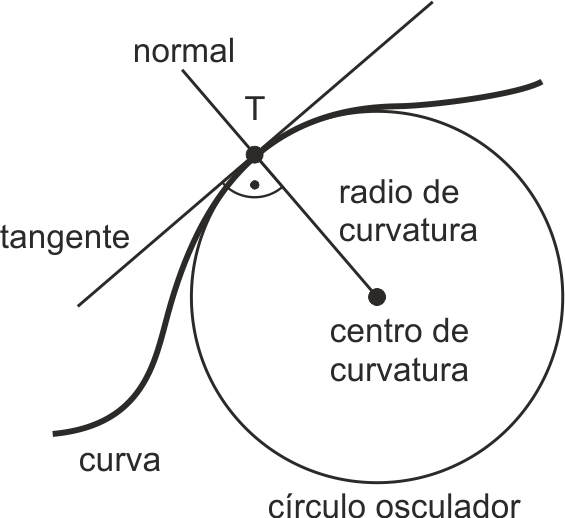
Normal. Círculo osculador

Si una recta es tangente a una curva, su perpendicular por el punto de tangencia se denomina normal a la curva en ese punto, y pasa por el centro de curvatura de la curva en ese punto.

En cualquier punto de la curva, es evidente – por la similitud del ejemplo con el círculo – que cuanto más acentuada sea la curva, menor será el radio de curvatura, y al contrario, cuando más suave sea la curva mayor será el radio de curvatura. Para cada punto de la curva, podemos considerar que existe una circunferencia cuyo centro es el centro de curvatura y cuyo radio es el radio de curvatura, y que se denomina círculo osculador (o circunferencia osculatriz) de la curva en ese punto. El circulo osculador toca al a curva en un solo punto, en el cual la tangente a la curva también es tangente al círculo.

Construcciones básicas de tangentes

Tangente a una circunferencia por uno de sus puntos

La tangente a una circunferencia por un punto P es perpendicular al radio de la circunferencia trazado desde ese punto.

Si en la construcción no tenemos acceso al centro de la circunferencia, hay un método alternativo: Con centro en P y radio arbitrario trazamos un arco que corte al arco principal en A. Con centro en A y el mismo radio trazamos un tercer arco que corte al principal en B. Con centro en P y radio PB trazamos otro que corte al tercer arco en el punto Q. Uniendo P con Q obtenemos la tangencia buscada.

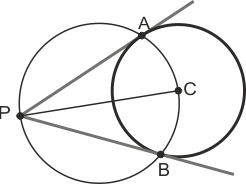
Tangentes a una circunferencia por un punto exterior

Trazamos el arco capaz de 90º del segmento que une el punto P con el centro C de la circunferencia (o, lo que es lo mismo, trazamos la circunferencia de diámetro PC). Esta circunferencia corta a la primera en los puntos de tangencia.

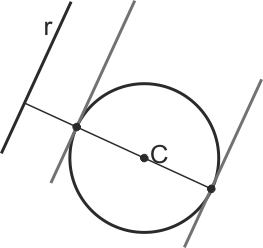
Tangentes a una circunferencia paralelas a una dirección (dada por la recta r)

Trazamos la perpendicular a r desde el centro C de la circunferencia. Esta recta corta a la circunferencia en los puntos de tangencia. Para encontrar las tangentes, trazamos paralelas por ellos a la recta r.

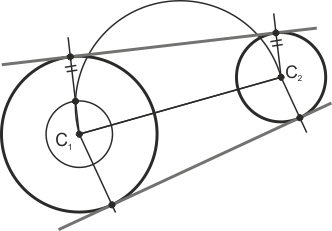
Tangentes comunes exteriores a dos circunferencias

Trazamos el arco capaz de 90º del segmento que une los dos centros. Con centro en el centro de la más grande, trazamos una tercera circunferencia de radio igual a la diferencia de los dos radios. Esta cortará al arco capaz en un punto que unido al centro dará los puntos de tangencia sobre la más grande. Para encontrar los puntos de tangencia en la pequeña, trazamos radios paralelos a los determinados por los puntos de tangencia en la grande.

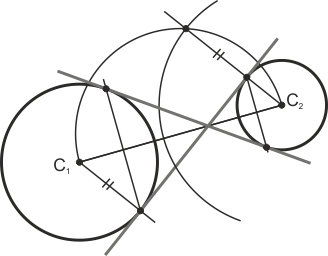
Tangentes comunes interiores a dos circunferencias

Trazamos el arco capaz de 90º del segmento que une los dos centros. Con centro en el centro de la más pequeña, trazamos una tercera circunferencia de radio igual a la suma de los dos radios. Esta cortará al arco capaz en un punto que unido al centro dará los puntos de tangencia sobre la más pequeña. Para encontrar los puntos de tangencia en la grande, trazamos radios paralelos e inversos a los determinados por los puntos de tangencia en la pequeña.

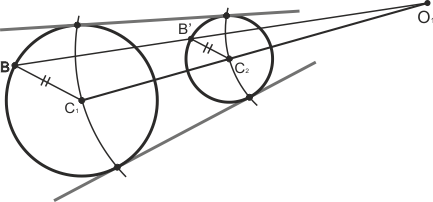
Tangentes exteriores comunes a dos circunferencias por homotecia

Tomamos un punto B cualquiera en una circunferencia (en el ejemplo lo hemos hecho en la grande) y trazamos su radio, y el radio paralelo a éste en la otra, dando el punto B’. Unimos B y B’ hasta cortar a la recta que une los centros, obteniendo el punto O₁ (centro de la homotecia directa que relaciona a ambas circunferencias). Por O₁ pasan las tangentes buscadas, que podemos trazar siguiendo el método visto en el primer ejemplo.

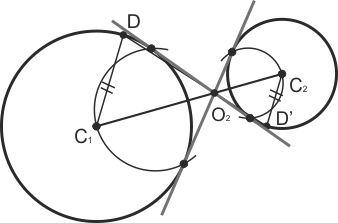
Tangentes interiores comunes a dos circunferencias por homotecia

Tomamos un punto D cualquiera en una circunferencia y trazamos su radio, y el radio paralelo pero inverso en la otra circunferencia, dando el punto D’. Unimos D y D’ hasta cortar a la recta que une los centros, obteniendo el punto O₂ (centro de la homotecia inversa que relaciona a ambas circunferencias). Por O₂ pasan las tangentes buscadas.

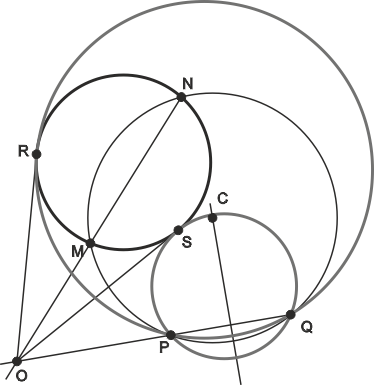
Circunferencias tangentes a otra y que pasan por dos puntos exteriores P y Q

Como la circunferencia buscada pasa por P y Q, su centro debe estar en la mediatriz de PQ. Sobre esta mediatriz tomamos un punto cualquiera C y tomándolo como centro trazamos una circunferencia que pase por P y Q. Esta corta a la circunferencia principal en los puntos M y N. Unimos M y N hasta cortar a la prolongación de PQ, obteniendo el punto O. Desde O se trazan las dos tangentes exteriores a la circunferencia principal, dando los puntos de tangencia R y S. R y S son los terceros puntos de las dos soluciones buscadas (circunferencias que pasan por P y Q).

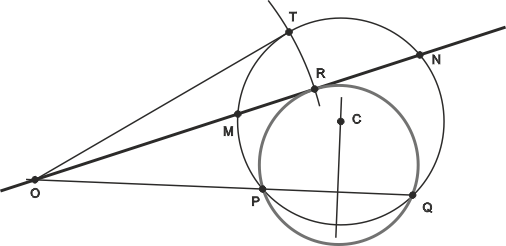
Circunferencia tangente a una recta y que pasa por dos puntos P y Q

Como la circunferencia buscada pasa por P y Q, su centro estará en la mediatriz de PQ. Sobre esta mediatriz tomamos un punto C cualquiera, y tomándolo como centro trazamos la circunferencia que pasa por P y Q. Esta circunferencia corta a la recta principal en dos puntos M y N. Unimos M y N hasta cortar la prolongación de PQ, obteniendo el punto O. Desde O trazamos una tangente a la circunferencia auxiliar, dando el punto de tangencia T. Abatiendo T sobre la recta mediante un arco de dentro O obtenemos R, tercer punto, junto con P y Q, de la solución.

La Inversión, que se estudia en el Bloque 2 de este libro, es una transformación geométrica plana que convierte rectas en circunferencias y viceversa, y tiene la propiedad de que conserva los puntos de tangencia. Por esa razón, tiene una aplicación especial en la simplificación y resolución de problemas de tangencias.

Tangencias en el espacio

El concepto de tangencia en el espacio se extiende, entre otras, a las siguientes relaciones:

• Una recta puede ser tangente en un único punto a una superficie curvada en el espacio. Si esta superficie forma parte de una figura de revolución como un cono o un cilindro, la recta tangente se cortará con una de las generatrices (o podrá coincidir con una de ellas).
• Un plano puede ser tangente a una superficie curvada en el espacio. Si esa superficie es de un cuerpo de revolución, la tangencia entre ambas superficies es una recta, que además coincide con una generatriz de la superficie de revolución.

Estos y otros casos se exponen de forma detallada en los capítulos dedicados a la geometría descriptiva.