Proyecciones de una esfera
Una esfera no presenta ninguna posición particular en el espacio. Sus proyecciones son siempre circunferencias de radio igual al radio de la esfera.
Esas circunferencias aparentes son curvas de contorno. En el caso de la proyección horizontal, la entendemos como la circunferencia horizontal contenida en la esfera de radio máximo, y en el caso de la proyección vertical, es la circunferencia frontal contenida en la esfera de radio máximo.
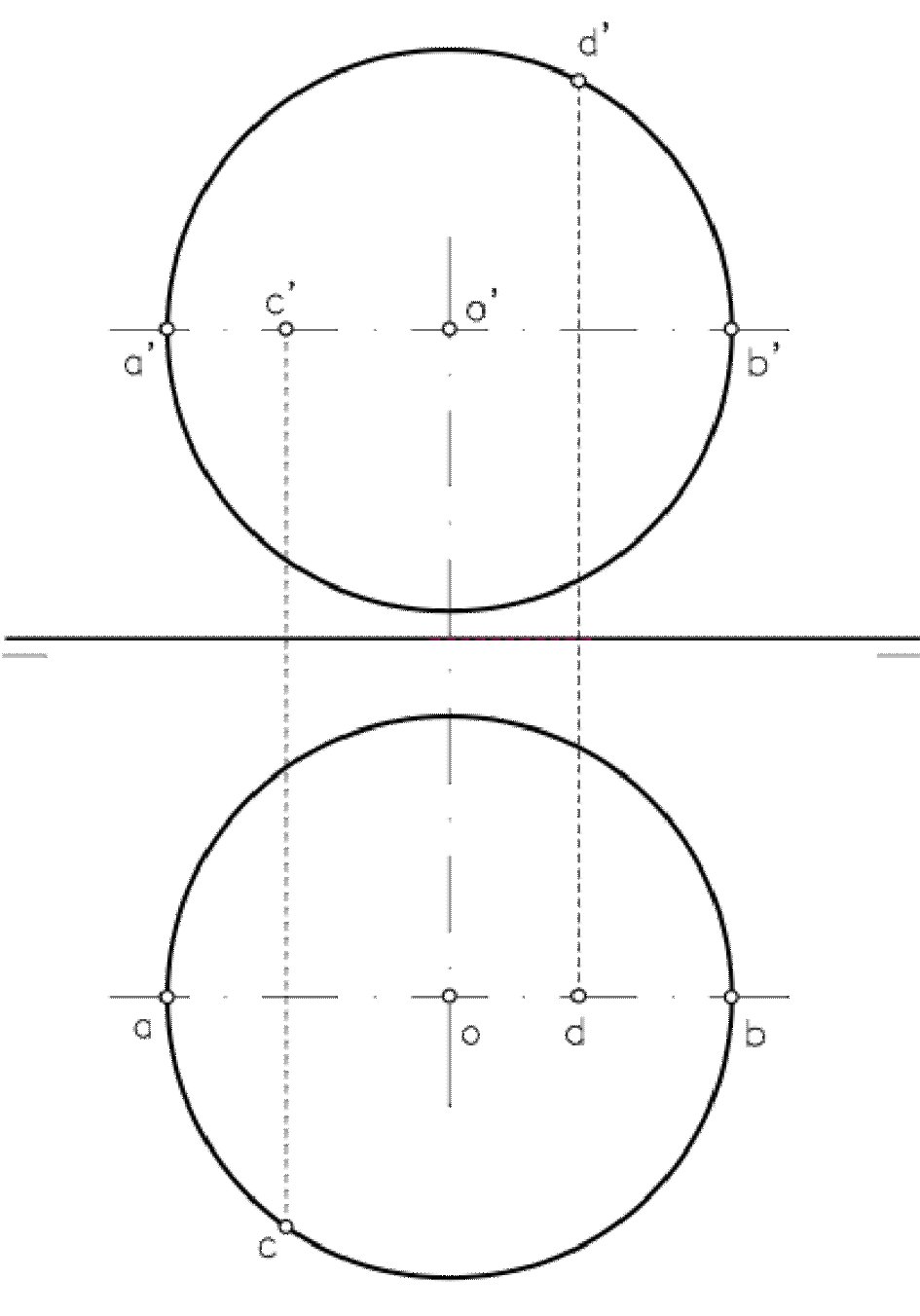
Círculos horizontales de la esfera (paralelos). Pertenencia de punto a esfera.
Se denominan paralelos a los círculos horizontales contenidos en la superficie de una esfera. Estos círculos se proyectan verticalmente como líneas horizontales, y horizontalmente como circunferencias.
Para determinar si un punto se encuentra en la superficie de una esfera, debemos comprobar que pertenece a uno de sus paralelos.
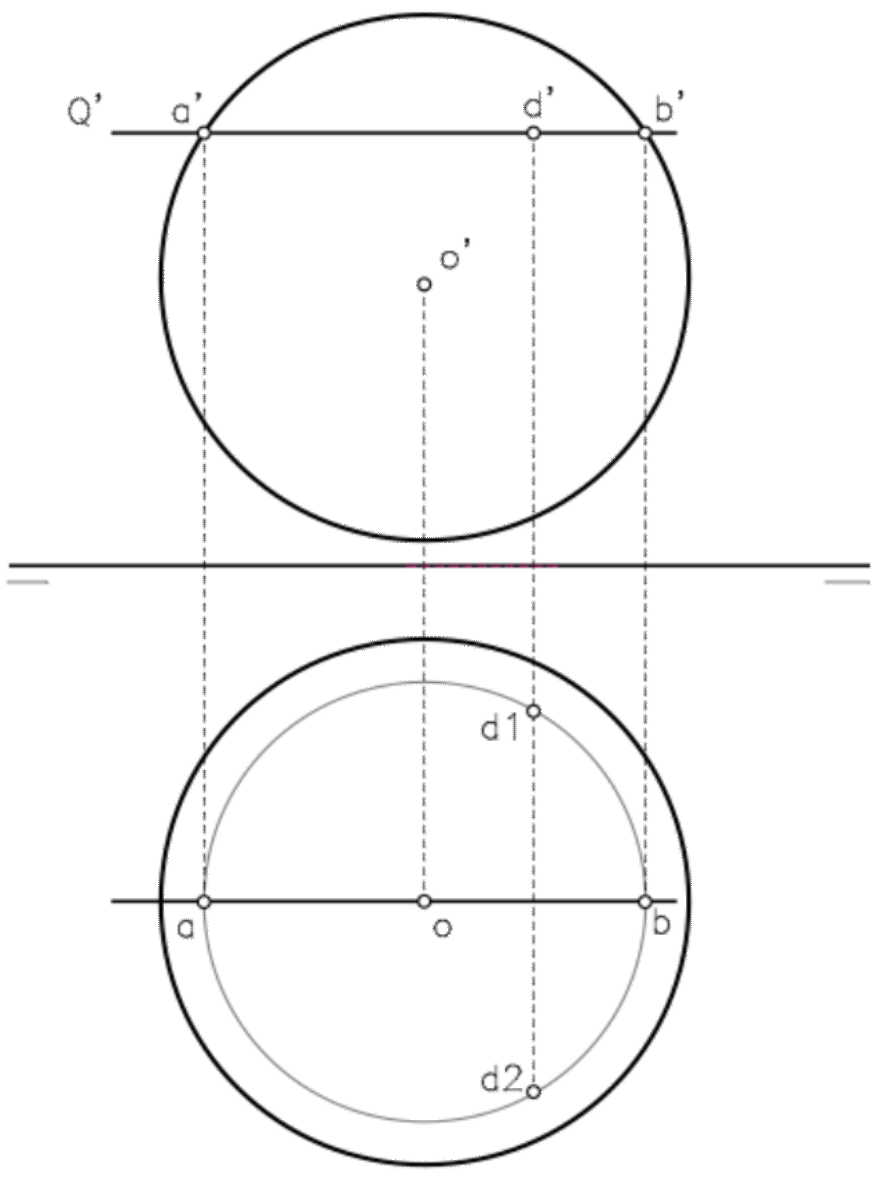
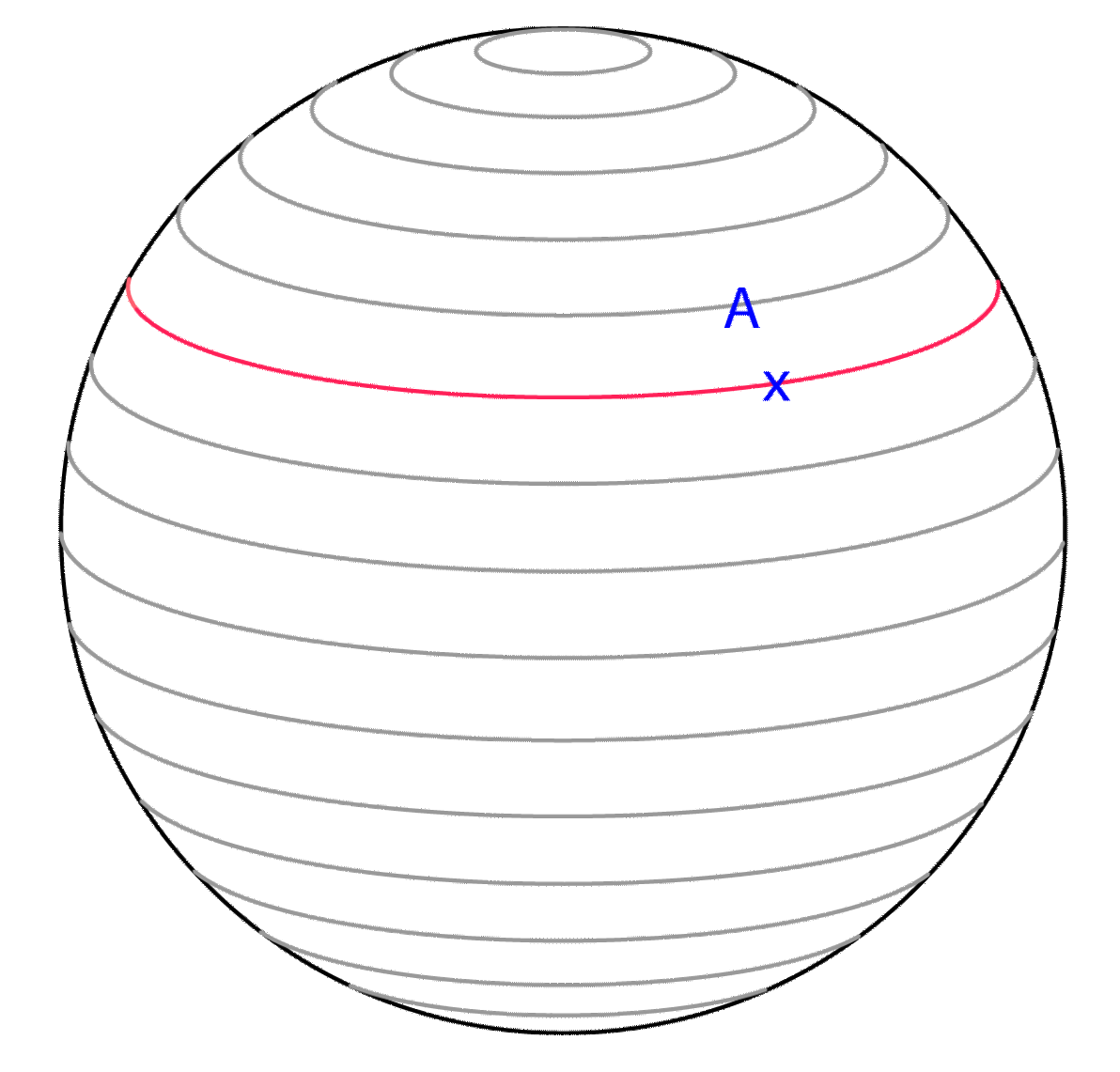
Los paralelos son elementos auxiliares que utilizaremos para resolver cualquier problema de secciones relacionados con la esfera.
Por analogía, existen círculos frontales en la superficie de la esfera, a los cuales se les puede dar el mismo uso.
La esfera y los giros o cambios de plano
Podemos deducir que cualquier cambio que hagamos en la esfera (giro o cambio de plano) no afectará a su aspecto. Por esa razón, es fácil aplicar en ella giros o cambios de plano para resolver problemas de situación o de intersecciones.
En el caso de los giros, habitualmente elegiremos un eje de giro a una recta vertical o de punta que pase por su centro, de forma que la esfera será invariable (no así sus puntos).
Secciones planas
Cualquier sección plana que se le practique a una esfera es un círculo, que se proyectará, de forma genérica, como dos elipses.
Si el plano es proyectante, la figura es inmediata, ya que en una de las proyecciones obtenemos el verdadero diámetro de dicha circunferencia, y basta llevarla a la otra proyección. Los puntos de tangencia de la segunda proyección con la proyección de la esfera pueden sacarse del circulo paralelo o frontal correspondiente.
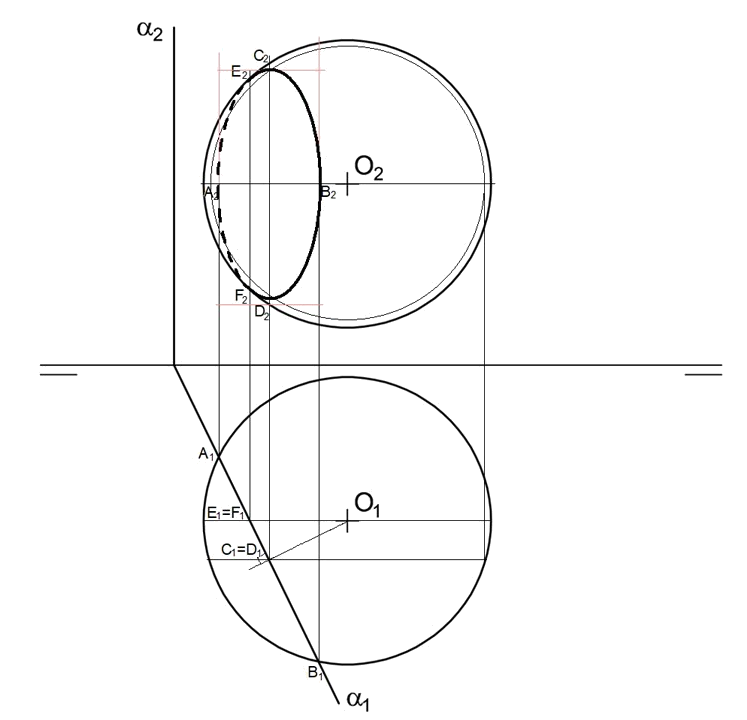
Para resolver la sección por un plano cualquiera, podemos tomar varios planos horizontales auxiliares, y cortarlos con el plano en cuestión, obteniendo varias líneas horizontales que a su vez cortaríamos con los paralelos de la esfera de igual cota. Para cada plano obtendríamos dos puntos. Este método no proporciona los elementos de las elipses, no obstante.
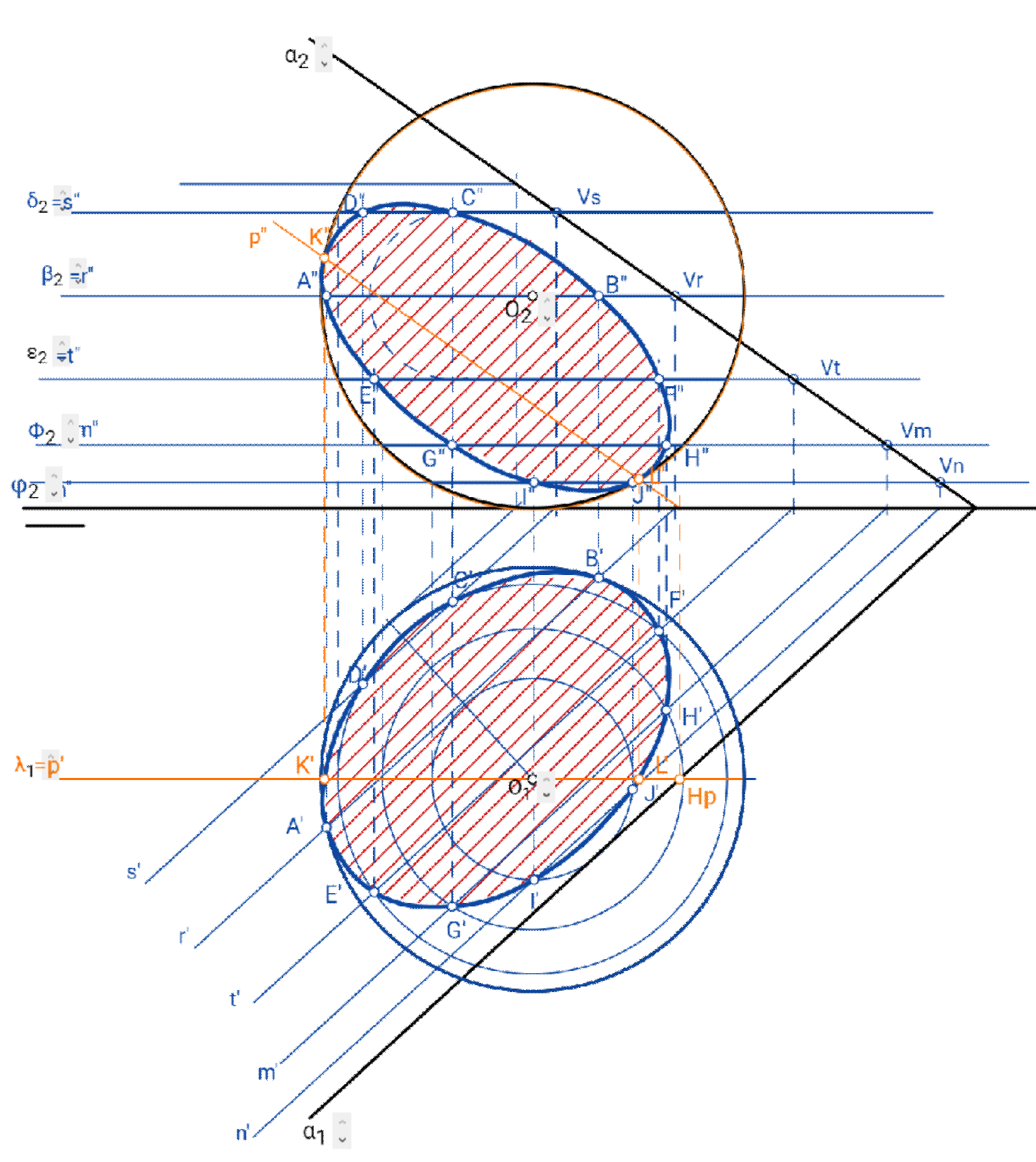
Es mejor método realizar un cambio de plano para colocar el plano de corte como proyectante. En esta figura lo hemos colocado proyectante vertical y hemos simplificado el problema.
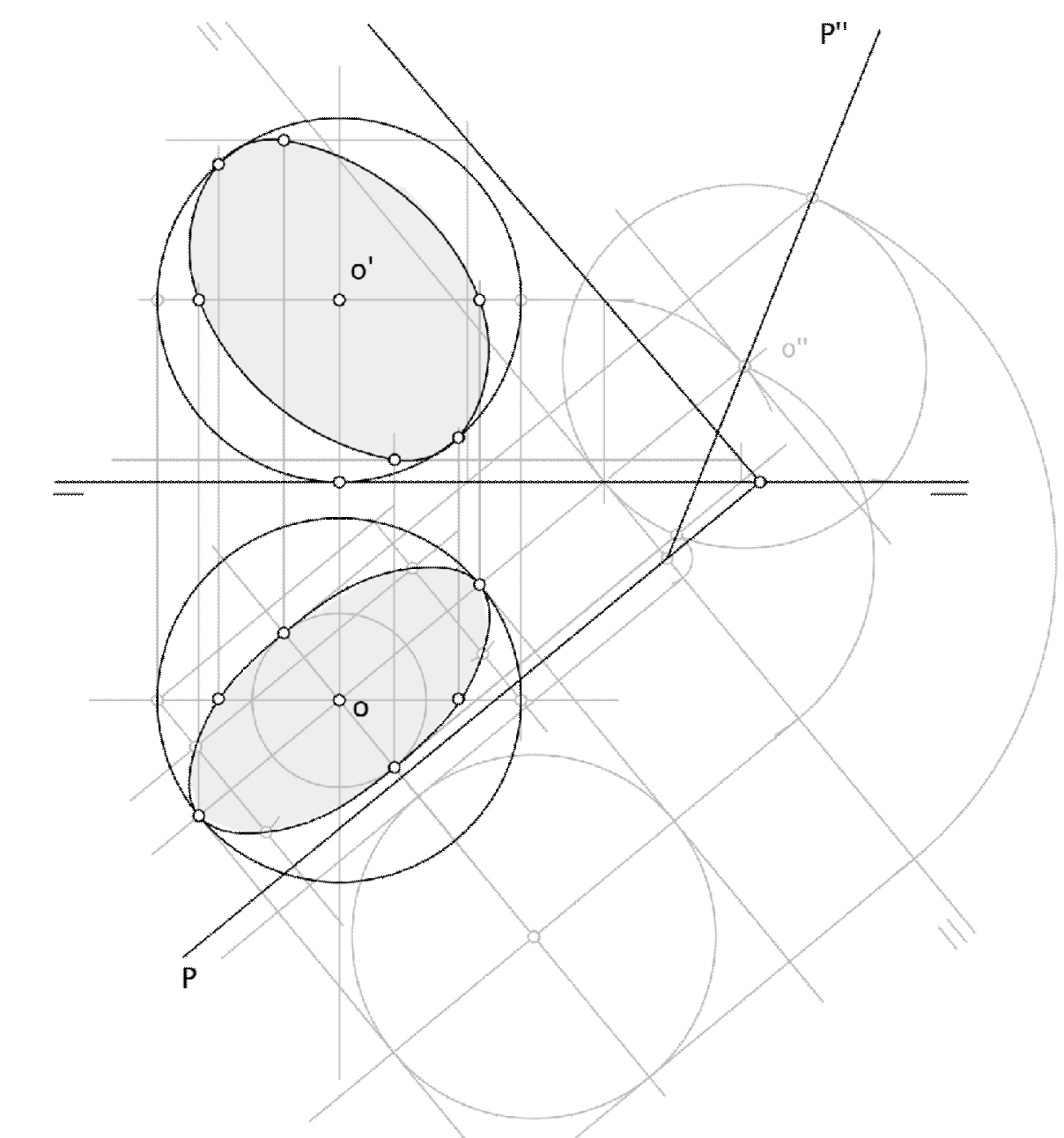
Corte con una recta
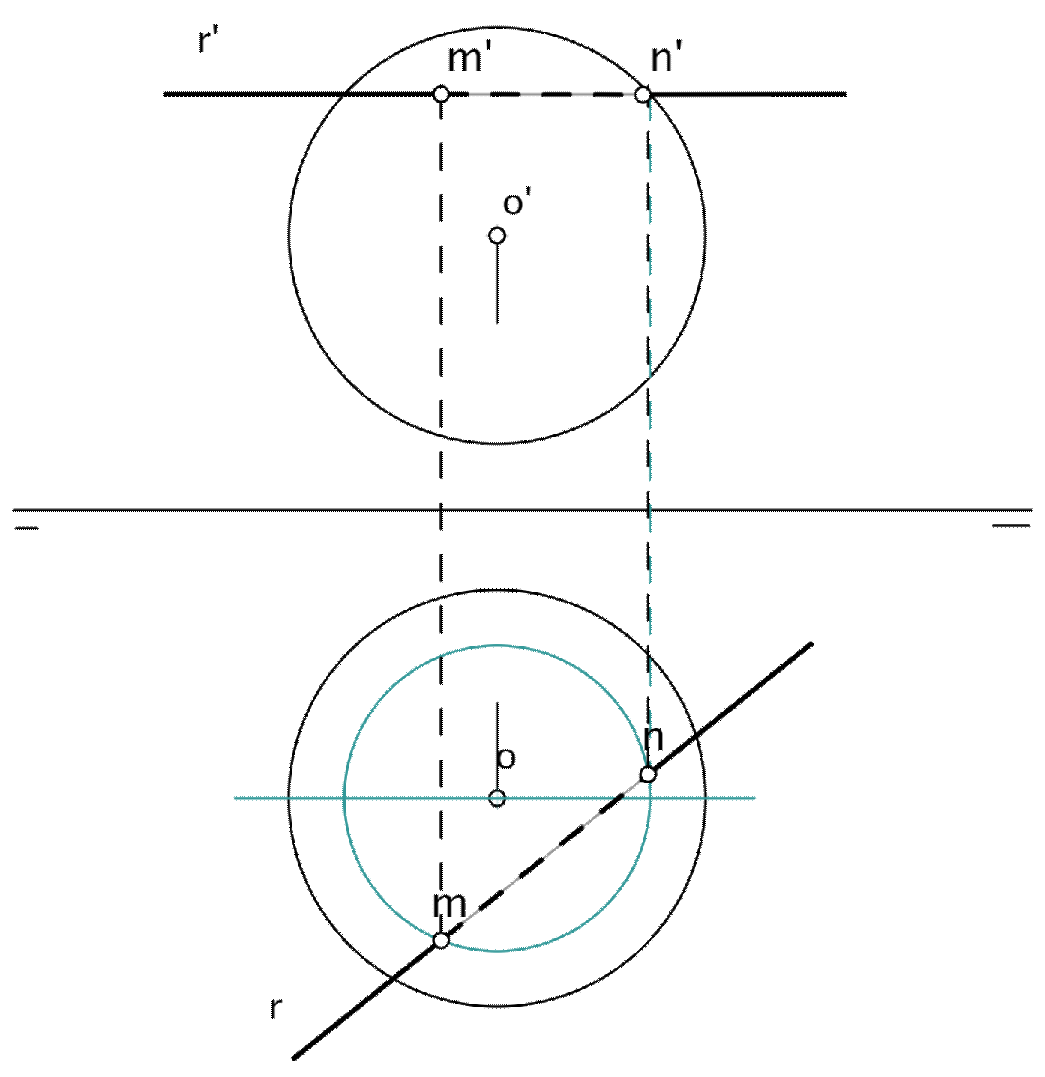
SI la recta es horizontal o frontal, el corte con la esfera es bastante simple, basta con cortar la proyección de la recta con el círculo horizontal o frontal de la esfera contenido en el plano proyectante donde está la recta.
Si la recta es oblicua, aplicando el método general podríamos contenerla en un plano proyectante, cortar éste con la esfera y luego cortar la figura resultante (elipse) con la recta. El problema es que el corte de la recta con la elipse deberíamos realizarlo por el método geométrico para obtener los puntos con precisión.
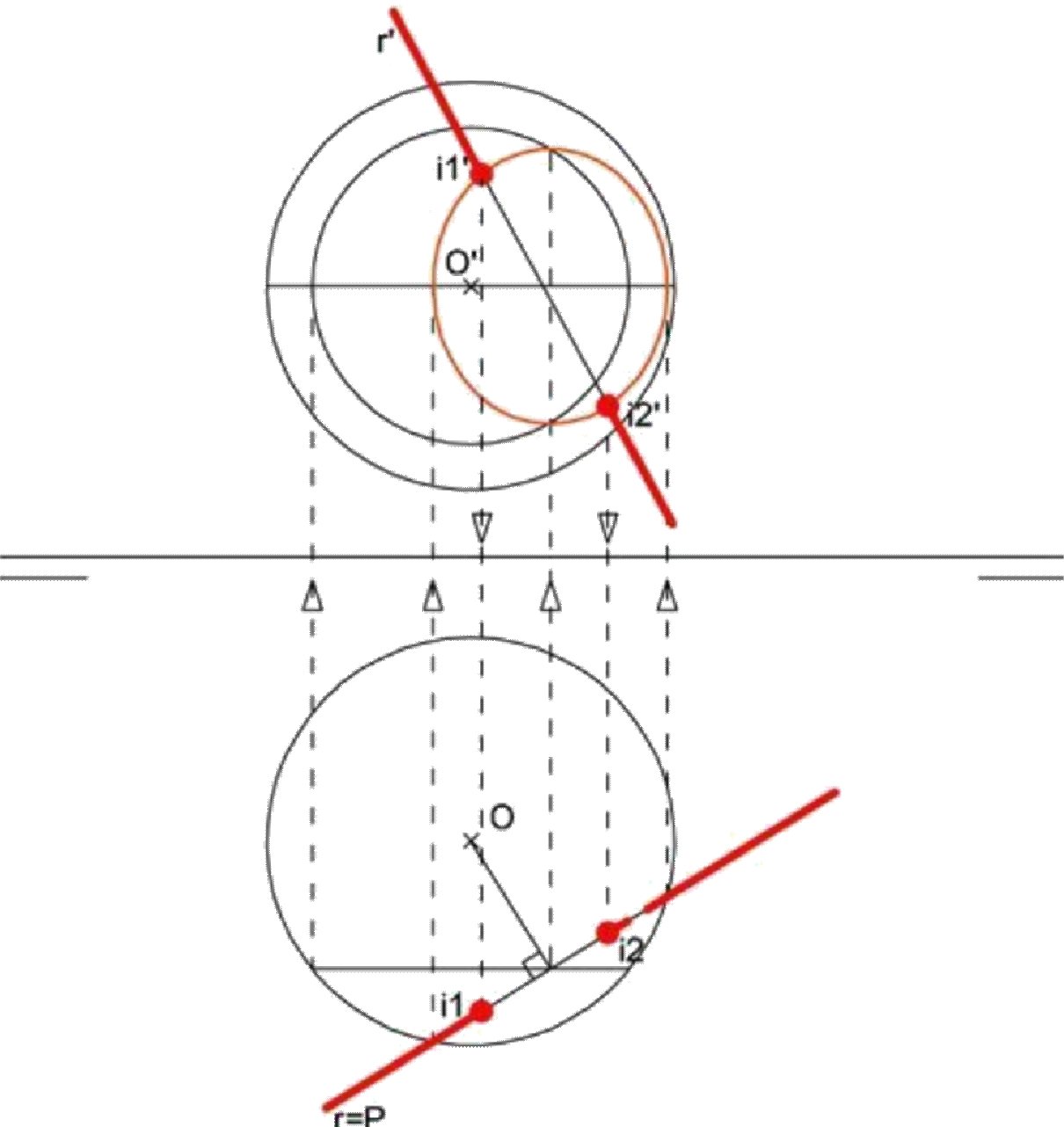
El mejor método consiste en girar la recta por un eje que pase por el centro de la esfera (de forma que la esfera quede invariable) hasta colocarla frontal u horizontal, y reducir el problema al caso inicial. En la figura, la recta pasa a ser horizontal después del giro.
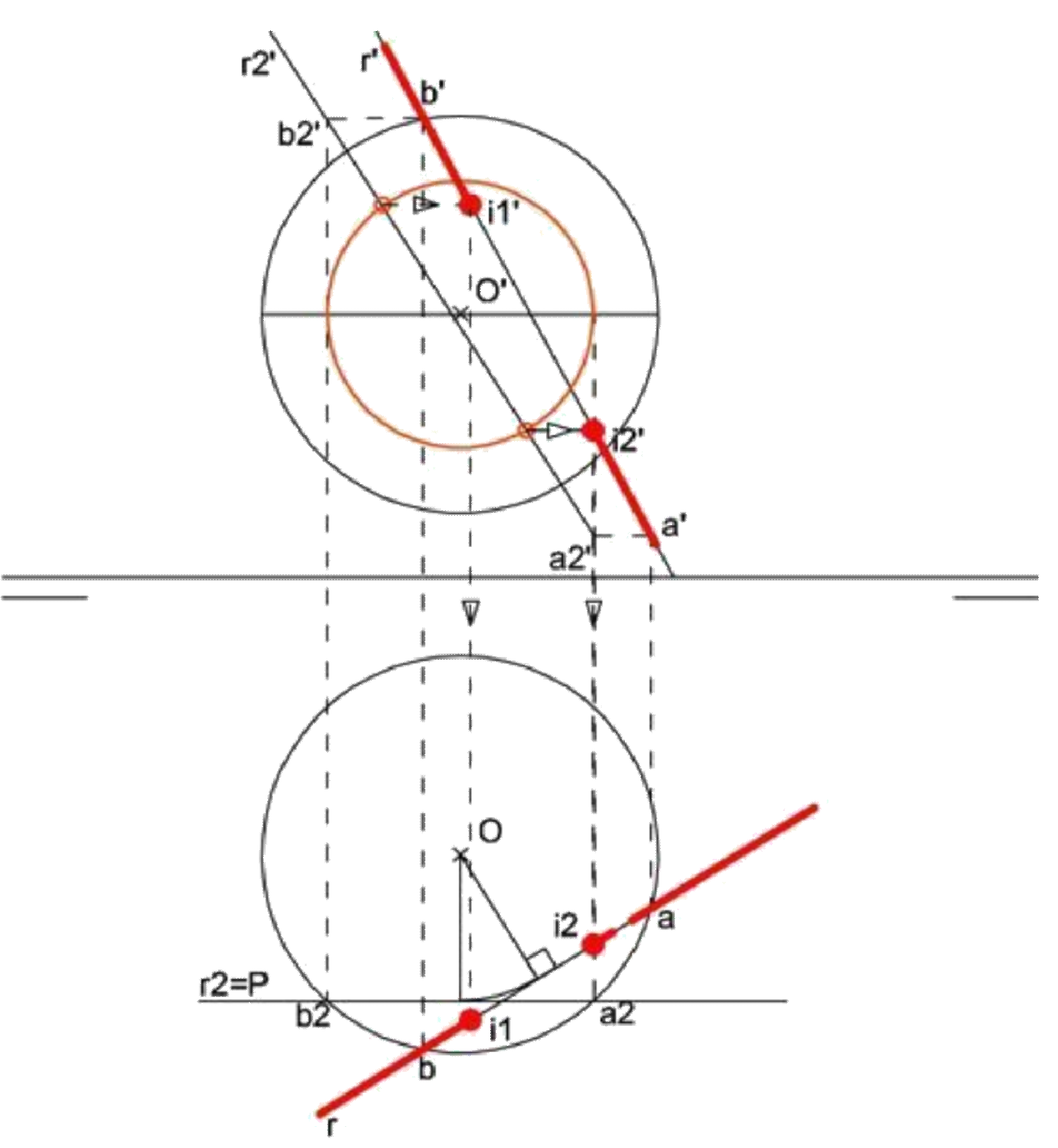
También podemos realizar un cambio de plano para colocar la recta de forma conveniente (en la figura, la hemos colocado horizontal).
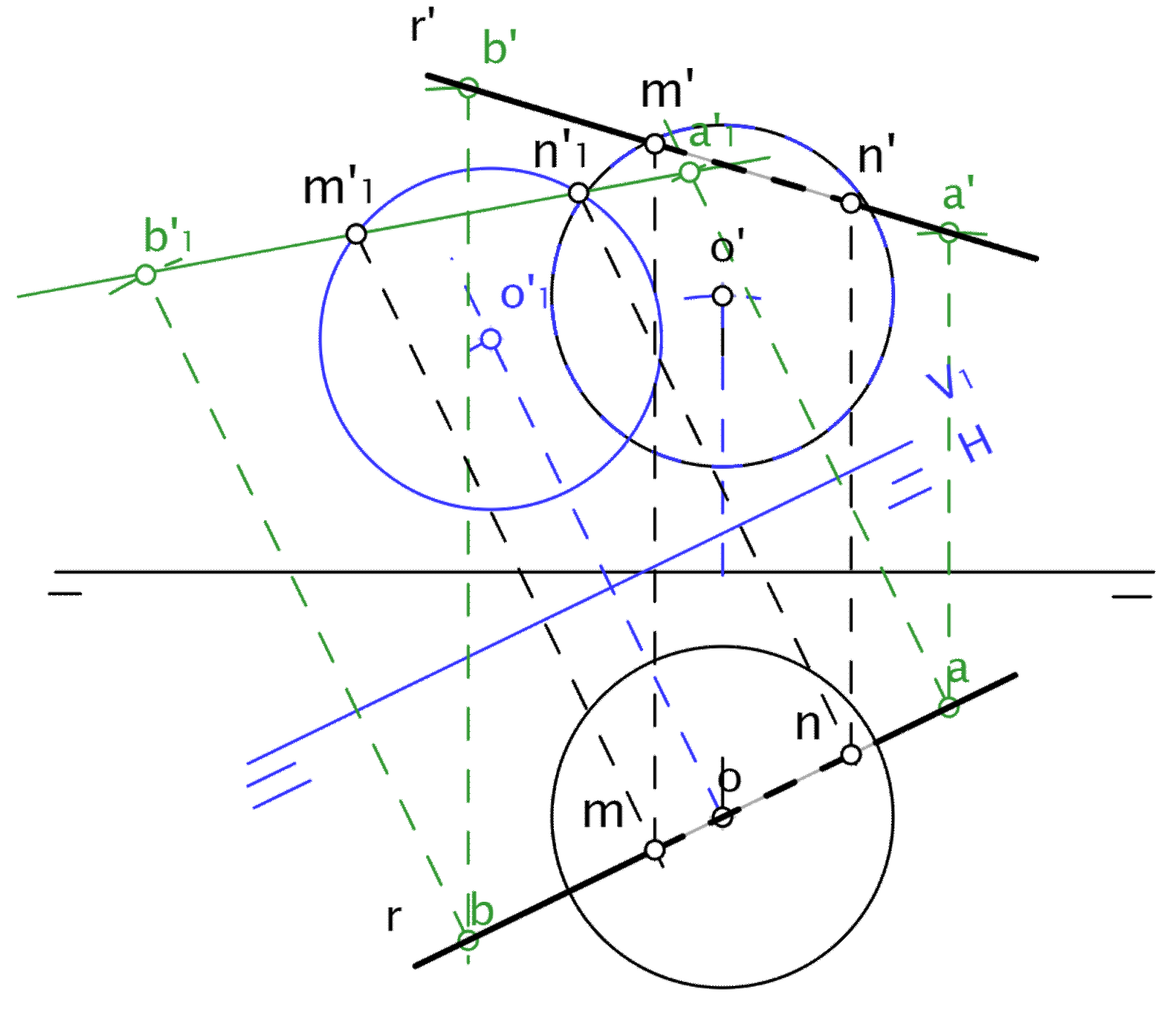
Plano y rectas tangentes a la esfera
En un plano tangente a una esfera, el punto de tangencia está en la perpendicular al plano desde el punto de tangencia hasta el centro de la esfera. Naturalmente, la longitud del segmento entre centro y punto de tangencia es igual al radio de la esfera.
Cualquier recta contenida en el plano que pase por ese punto de tangencia también es tangente a la esfera.
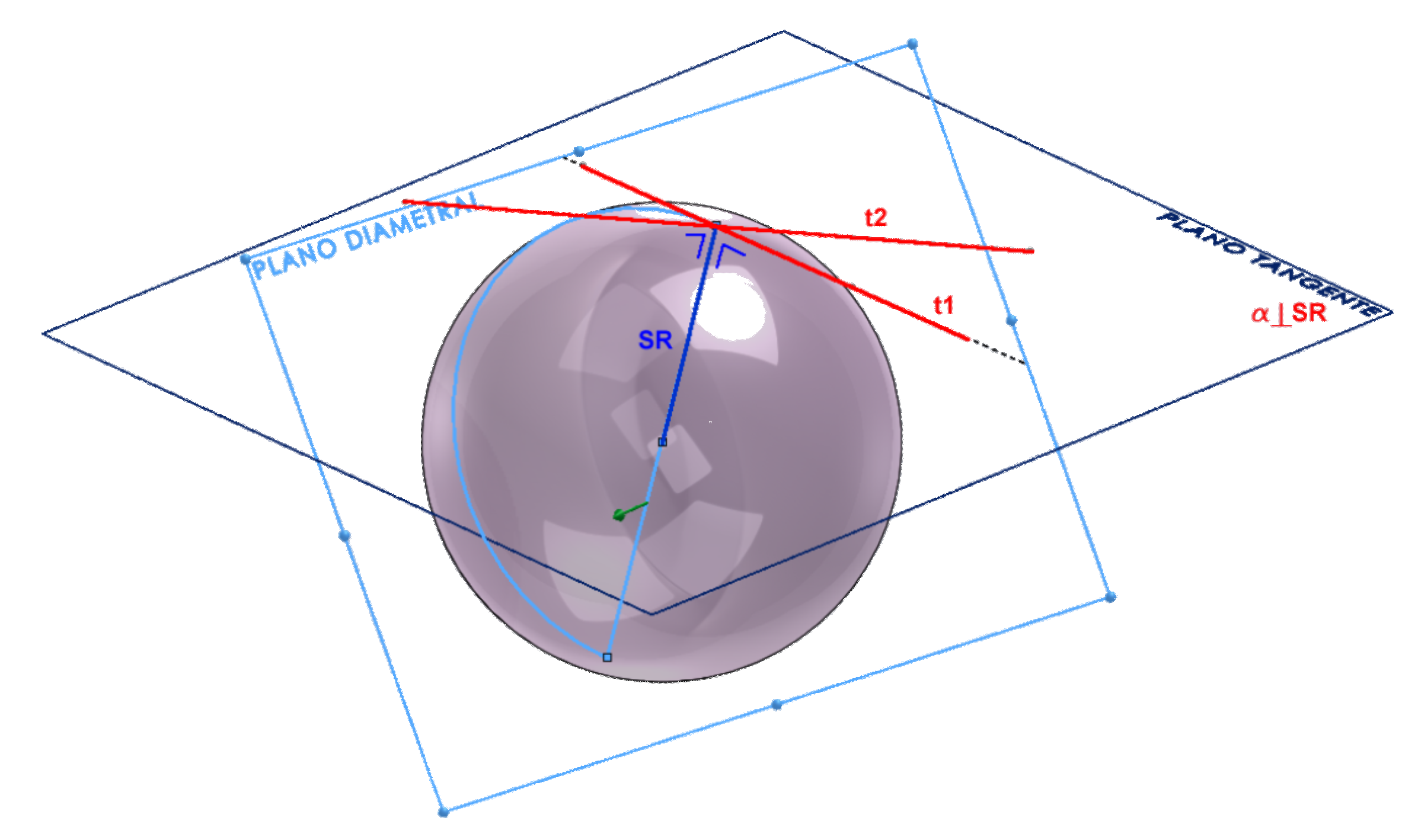
Así, para resolver los problemas de tangencias, aplicamos los conceptos conocidos de recta perpendicular al plano y de distancias o longitudes de segmentos. En la figura, el plano tangente a la esfera en el punto A es el plano perpendicular por dicho punto a la recta que une el centro de la esfera O con A.
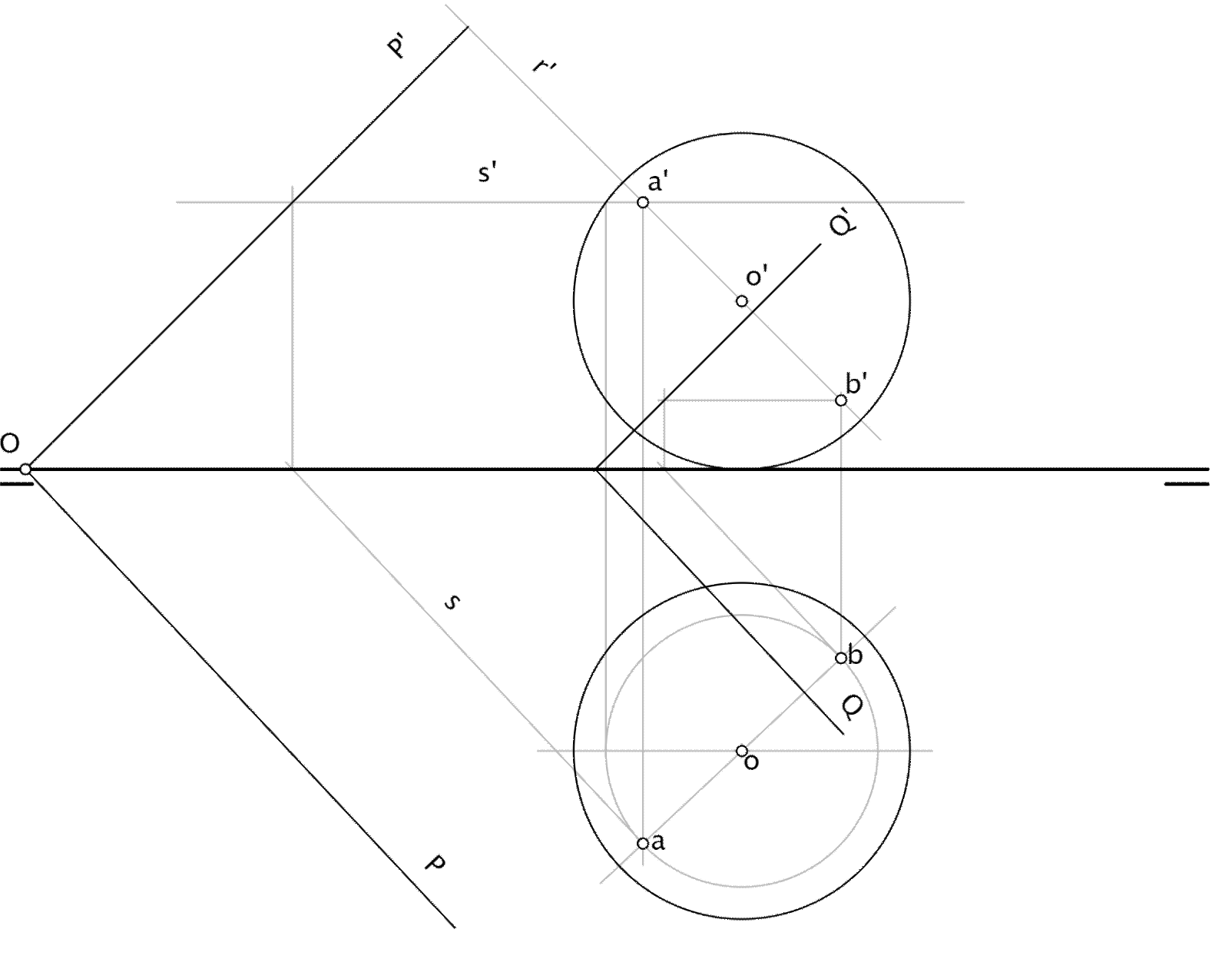
Si el plano tangente es proyectante, en una de las proyecciones tendremos que su traza es tangente a la proyección de la esfera. Así, es bastante evidente que podemos intentar reducir los problemas de tangencia a casos en los que el plano sea proyectante, mediante giros o cambios de plano.
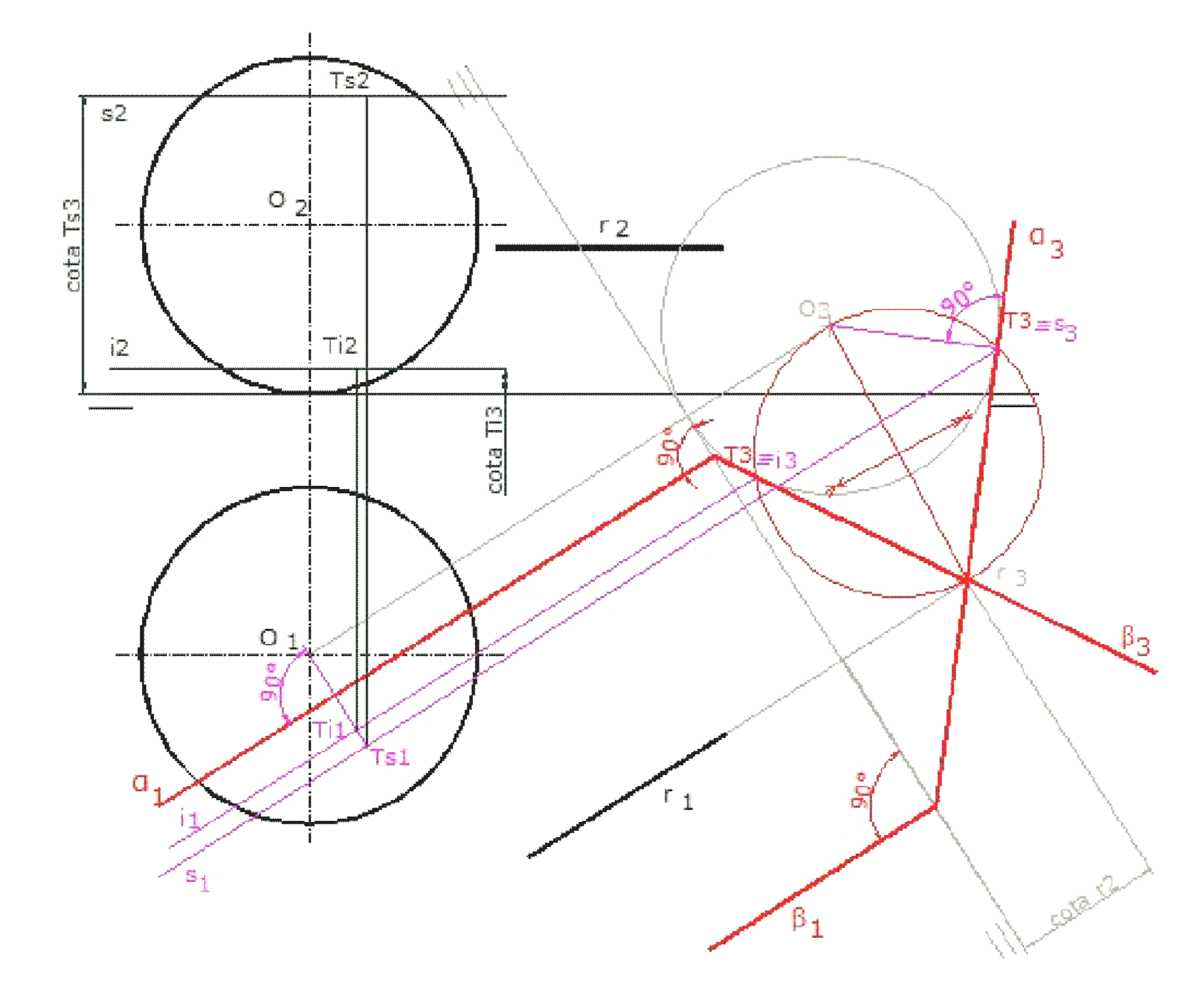
En este ejemplo, hemos encontrado dos planos tangentes a la esfera que contienen una recta exterior r. Para ello hemos hecho un cambio de plano tal que convierte a la recta en recta de punta, de forma que los planos tangentes sean proyectantes verticales (hay dos soluciones).
Desarrollo de la esfera
La esfera no es una figura desarrollable, ya que su superficie no puede mostrarse en una superficie plana equivalente, tal y como ocurre con los conos y los cilindros.
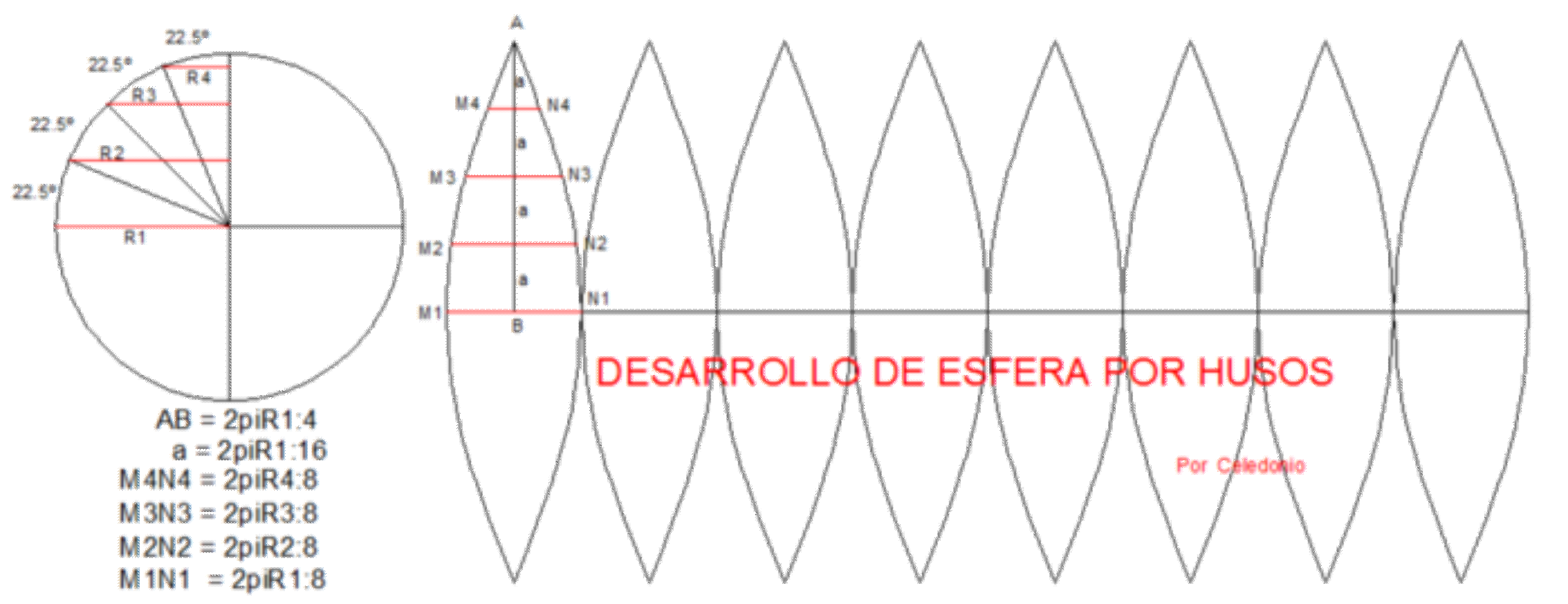
No obstante, existe la necesidad de desarrollar la esfera terrestre en superficie plana, para poder representar su superficie (mapas). Por ello, hay varios métodos que, con mayor o menor acierto, permiten dicho desarrollo. El método de los husos proporciona una buena aproximación, pero tiene el inconveniente de que separa en partes la superficie desarrollada.
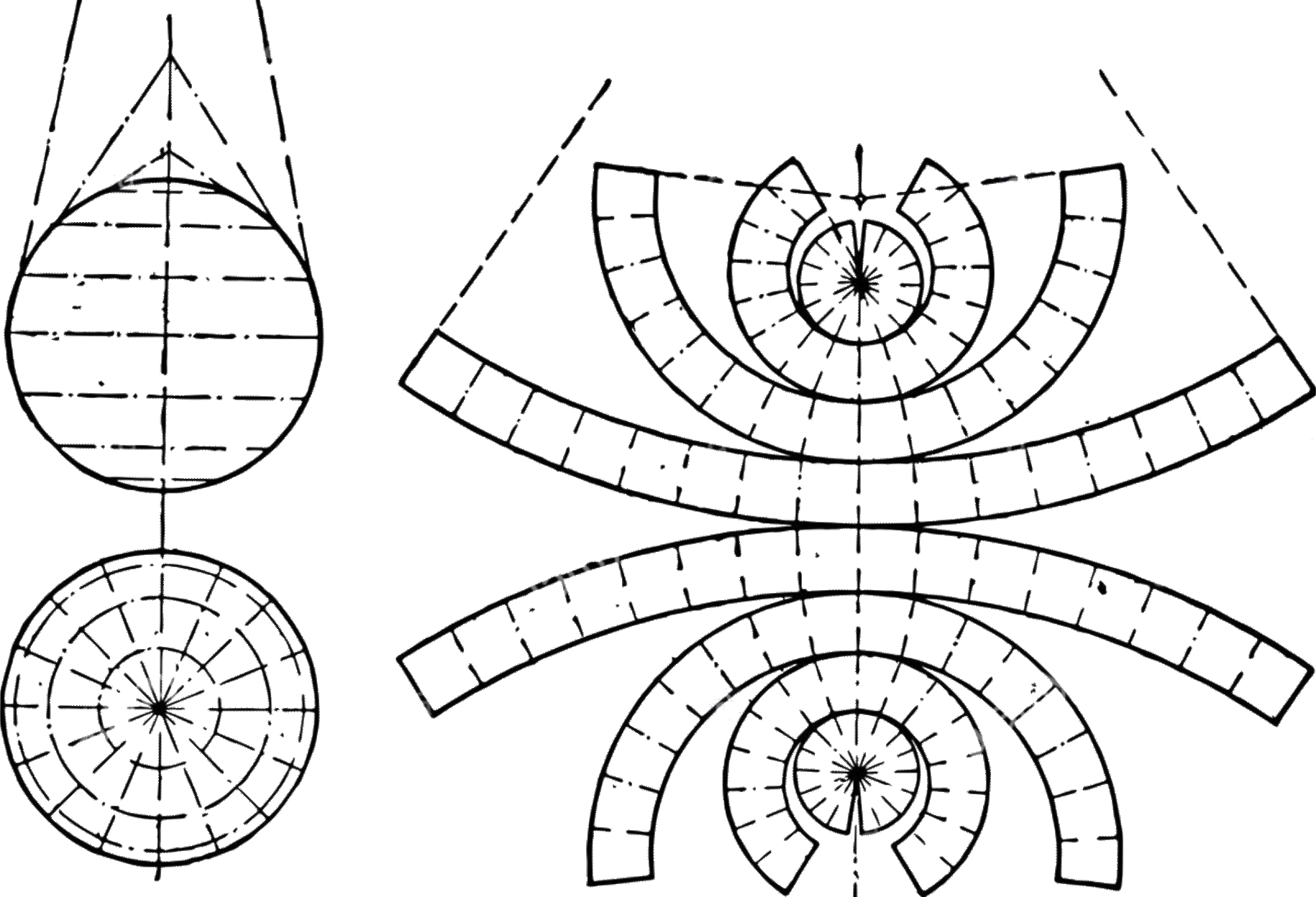
Este otro método consiste en dividir la esfera en secciones horizontales.
Lo que vemos en los mapas no son desarrollos, en realidad son proyecciones, y como tales están deformadas. La más habitual es la proyección cilíndrica, cuya deformación (ampliación) se va acentuando conforme nos alejamos del ecuador.
