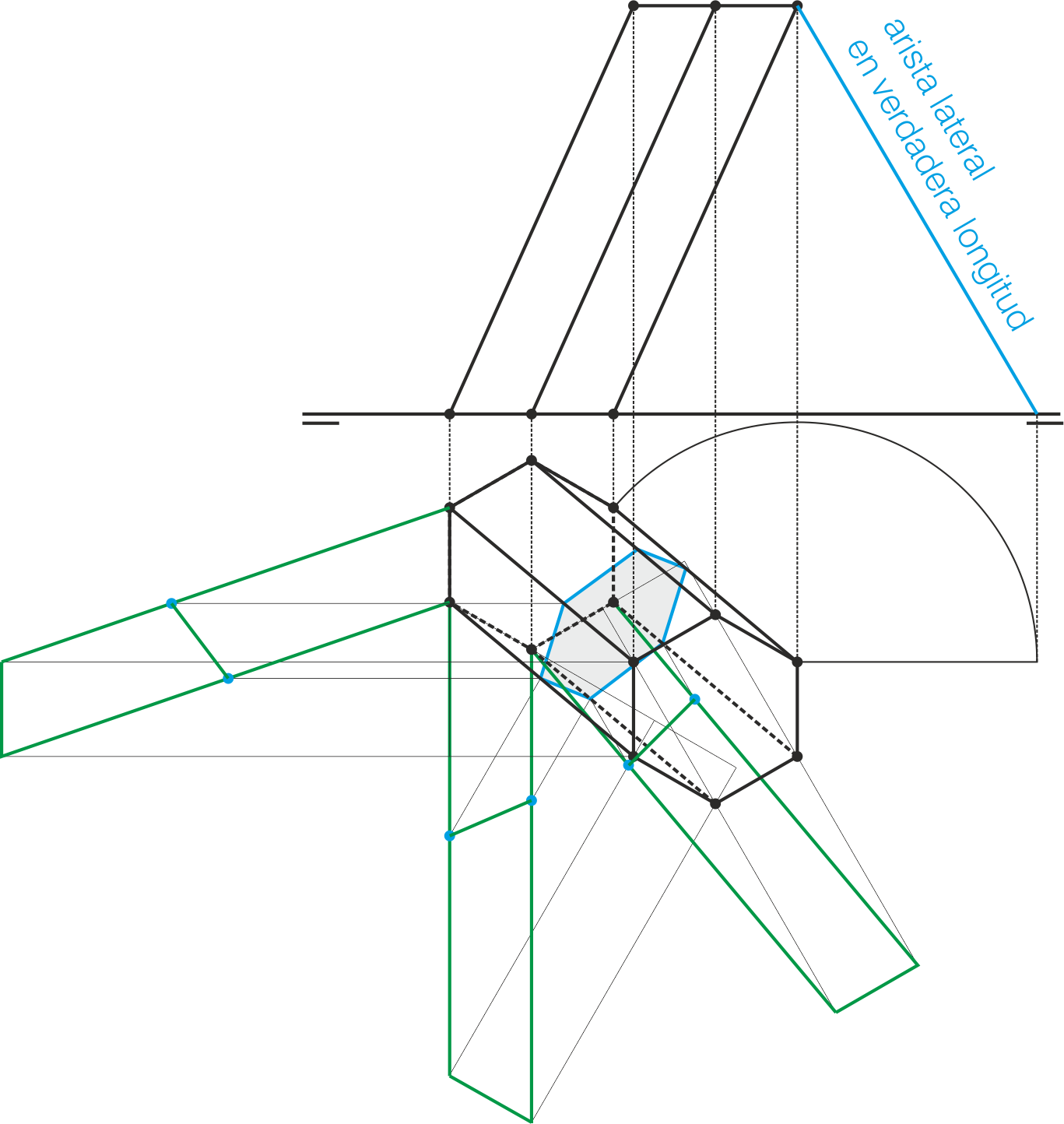
Descripción y Elementos

Un prisma es un poliedro en el cual existen varias caras (al menos 3) que son cuadriláteros y que tienen dos lados (los compartidos por dos caras contiguas) paralelos. Estas caras se llaman caras laterales, y las aristas paralelas, aristas laterales.

Limitando al prisma existen dos bases, una superior y otra inferior, que son polígonos cuyo número de lados es igual al número de caras laterales. Las aristas de estas bases se denominan aristas básicas.

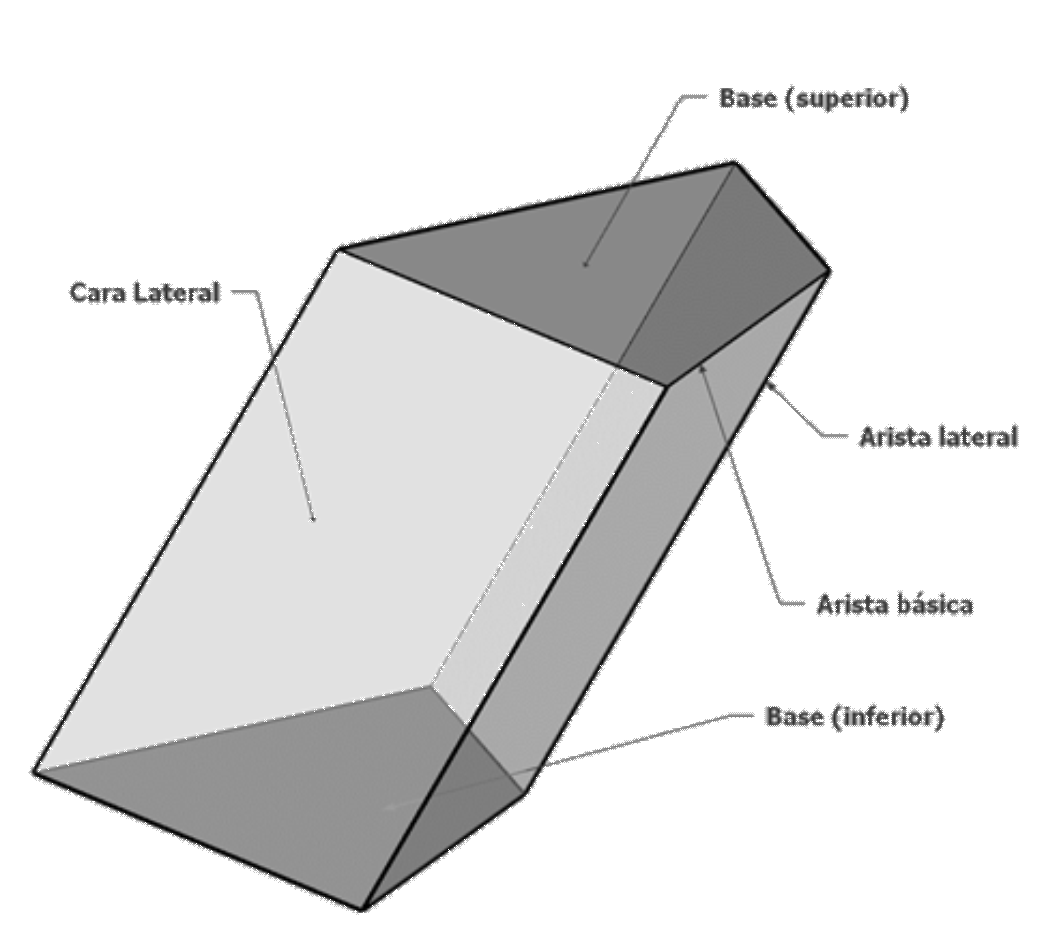
Si las dos bases del prisma son polígonos regulares (iguales y paralelos), el prisma es regular.

Si las dos bases son paralelas (e iguales, por tanto), la altura del prisma se define como la distancia entre estas bases.

Si en un prisma de bases paralelas las aristas laterales son perpendiculares a ellas, el prisma se denomina recto, y en caso contrario es oblicuo.

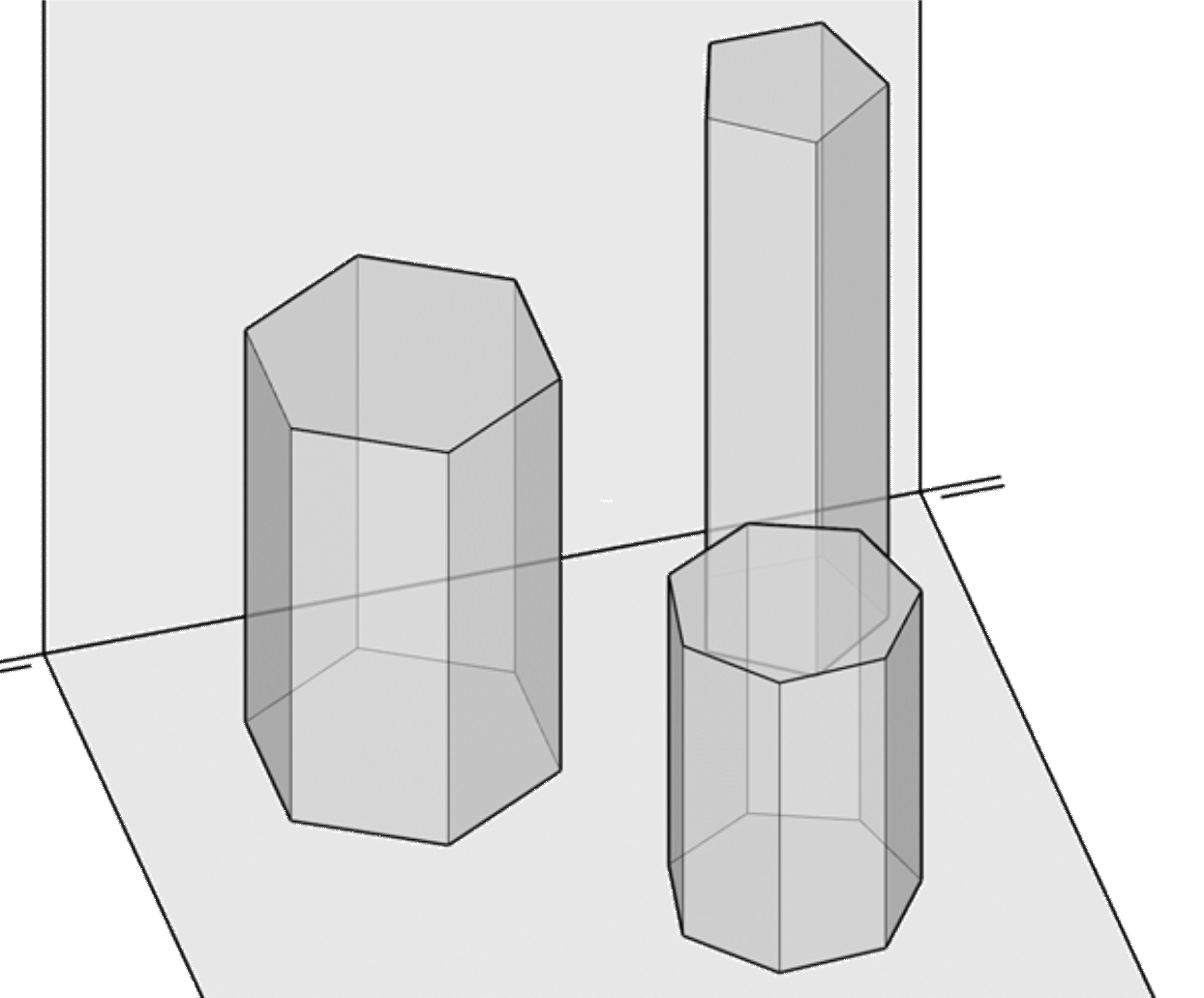
Si las bases de un prisma no son paralelas, al prisma se le denomina truncado.

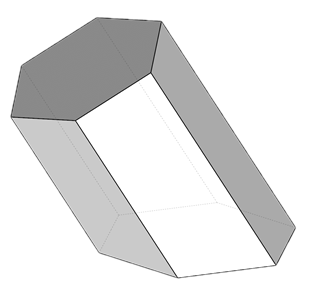
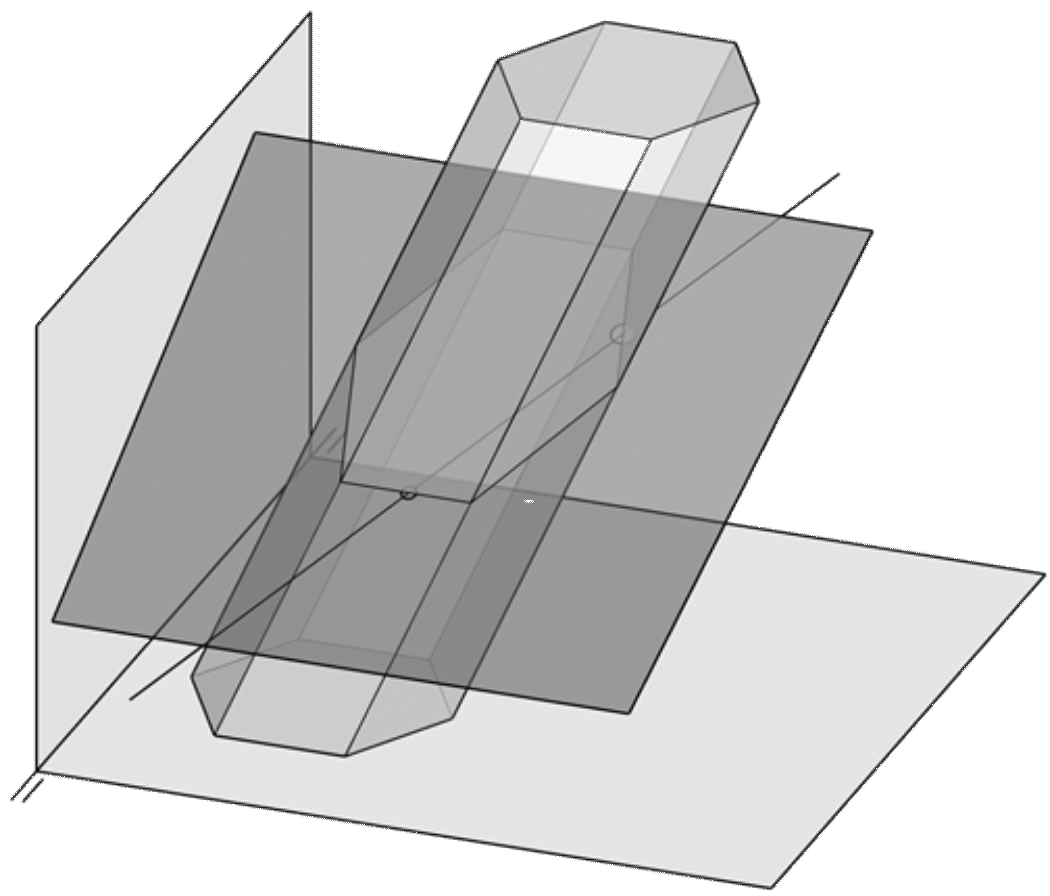
Plano rasante

Es un plano que contiene a una de las aristas laterales.

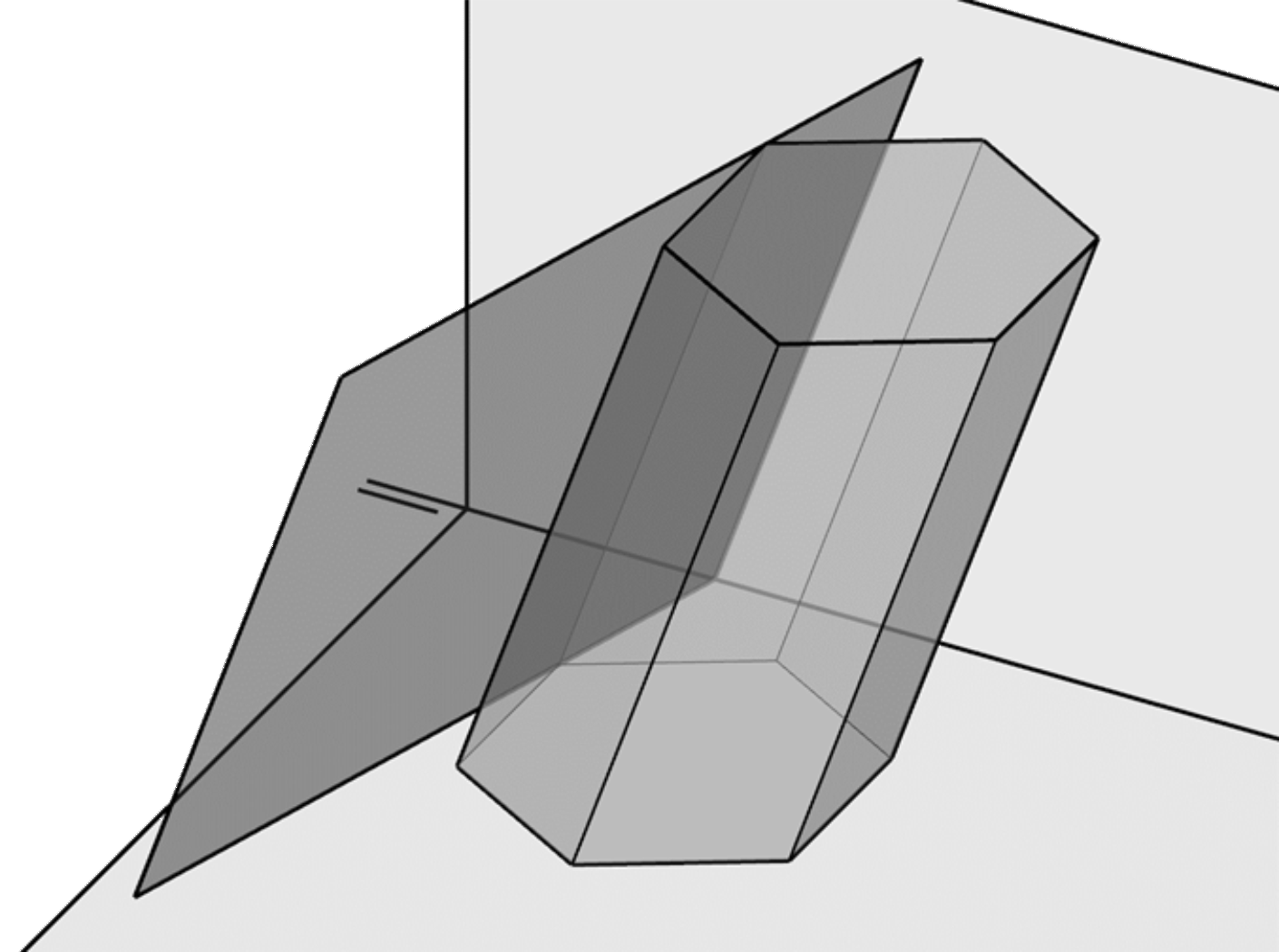
Sección plana

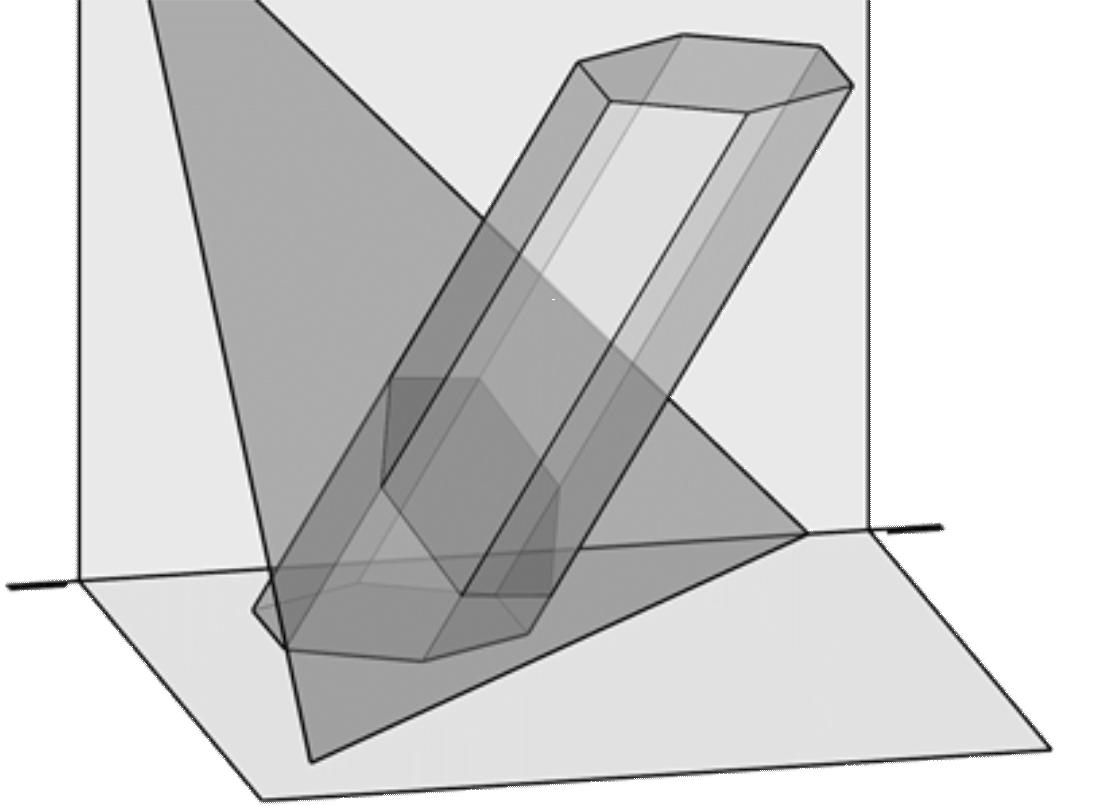
Al cortar un prisma por un plano se obtiene un polígono de igual número de lados que caras laterales tiene. Existe una relación de afinidad espacial entre una sección plana y la base de un prisma. En esta afinidad, la dirección es la de las aristas laterales, y el eje es la traza horizontal del plano de corte. Esta afinidad puede ayudar a encontrar el polígono de la sección.

Si el plano es oblicuo, puede hacerse un giro o cambio de plano para convertirlo en proyectante, encontrar la sección en el nuevo sistema y hacer un cambio de plano (o giro) inverso para encontrarla en las proyecciones originales.

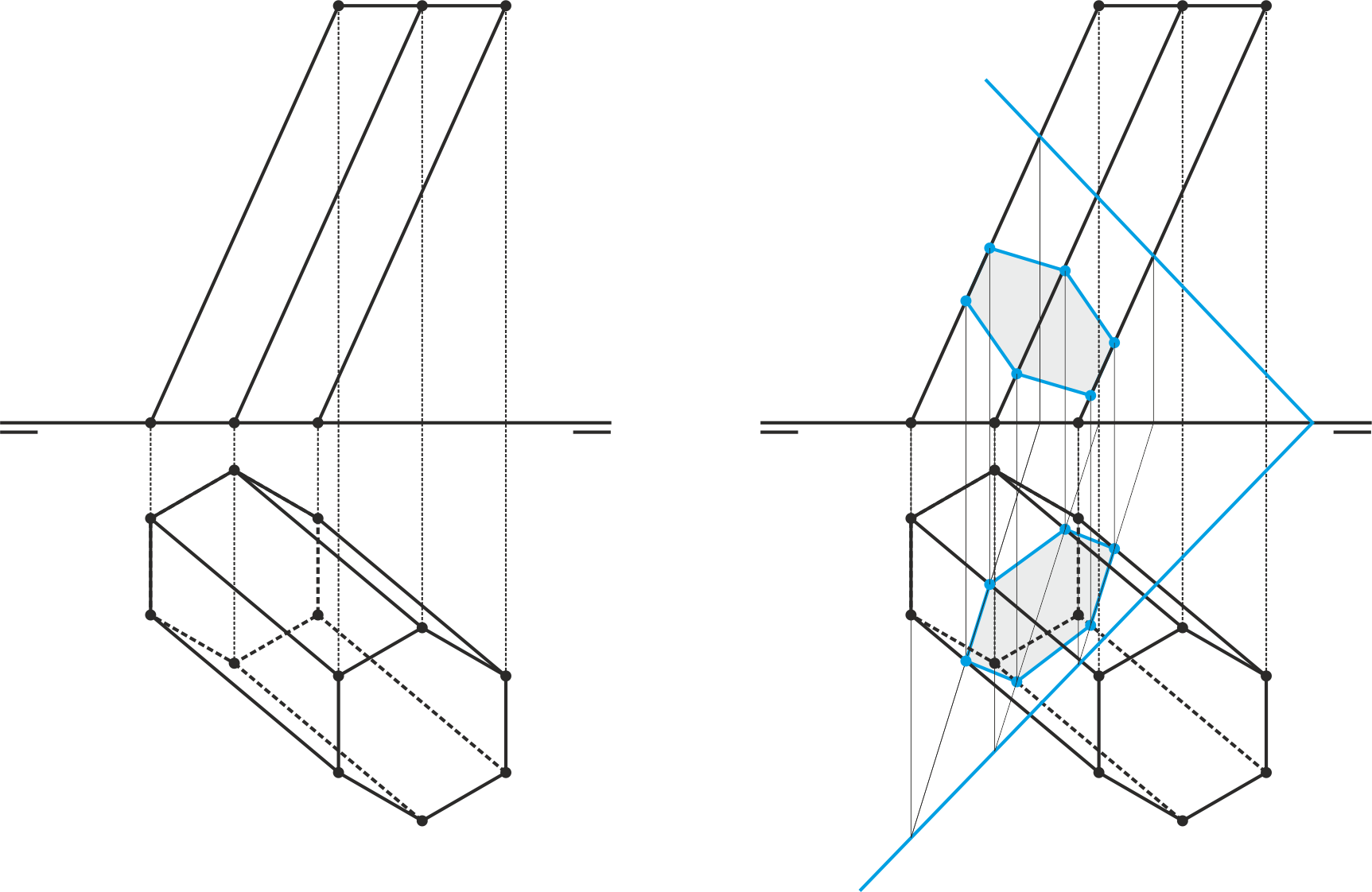
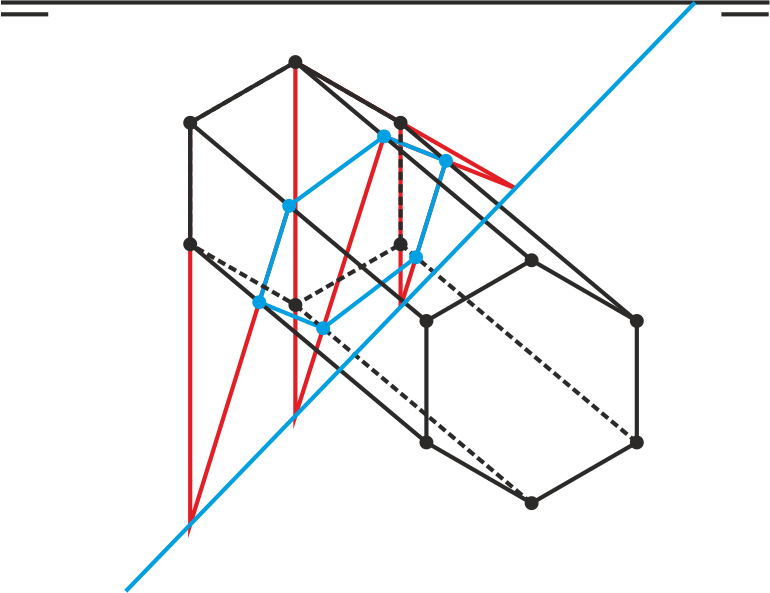
Corte con una recta

Para cortar un prisma con una recta se busca un plano auxiliar que contenga a la recta y sea paralelo a las aristas laterales. Este plano se cortará con el prisma en un paralelogramo, coplanario con la recta, que se cortará con ella en dos puntos (entrada y salida).

También, igual que en los cuerpos estudiados en capítulos anteriores, podemos contener la recta en un plano auxiliar proyectante, que definirá una sección poligonal. La intersección de esa sección con la recta proporciona los puntos buscados.

Desarrollo, Transformada y Geodésica

El desarrollo de un prisma se realiza de forma similar al de la pirámide, adosando las caras laterales por las aristas laterales, y dibujando las bases adosadas a alguna de las caras laterales.

Lo explicado en el caso de la pirámide en lo que respecta a transformada y geodésica es de igual aplicación en el caso de los prismas.