Rectas paralelas

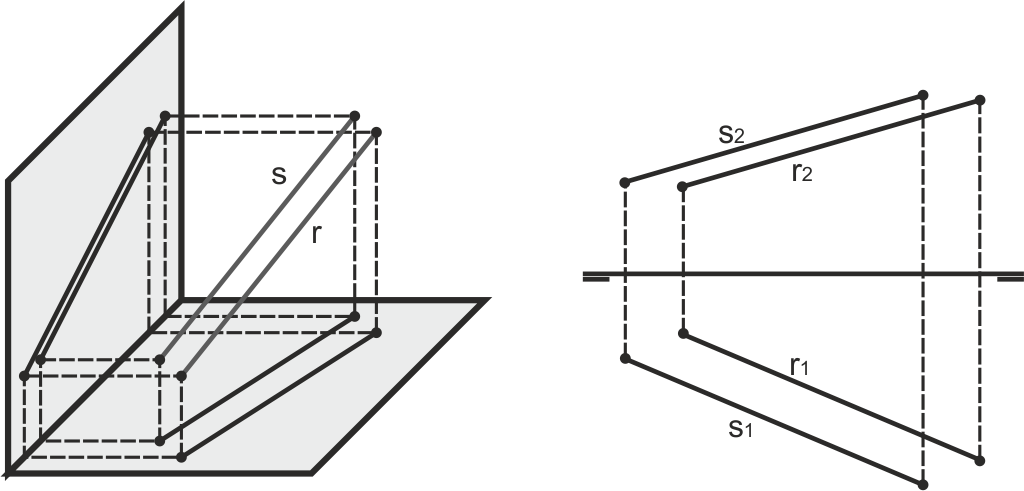
En el capítulo dedicado a la recta ya vimos que cuando dos rectas son paralelas sus proyecciones son paralelas dos a dos. Para trazar una recta paralela a otra por un punto exterior, basta con dibujar las proyecciones paralelas a las de la primera por ese punto.

Planos paralelos

En el capítulo dedicado al plano también pudimos ver que las trazas de dos planos paralelos también lo son dos a dos.

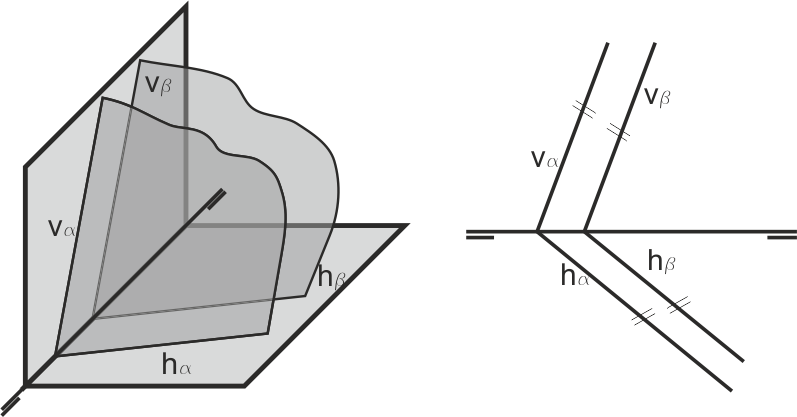
Para encontrar un plano paralelo a otro por un punto exterior, basta con trazar una horizontal del nuevo plano (sabiendo la dirección que va a tener su traza horizontal), cuya traza determinará por donde va a pasar la traza vertical del nuevo plano.

Recta paralela a un plano

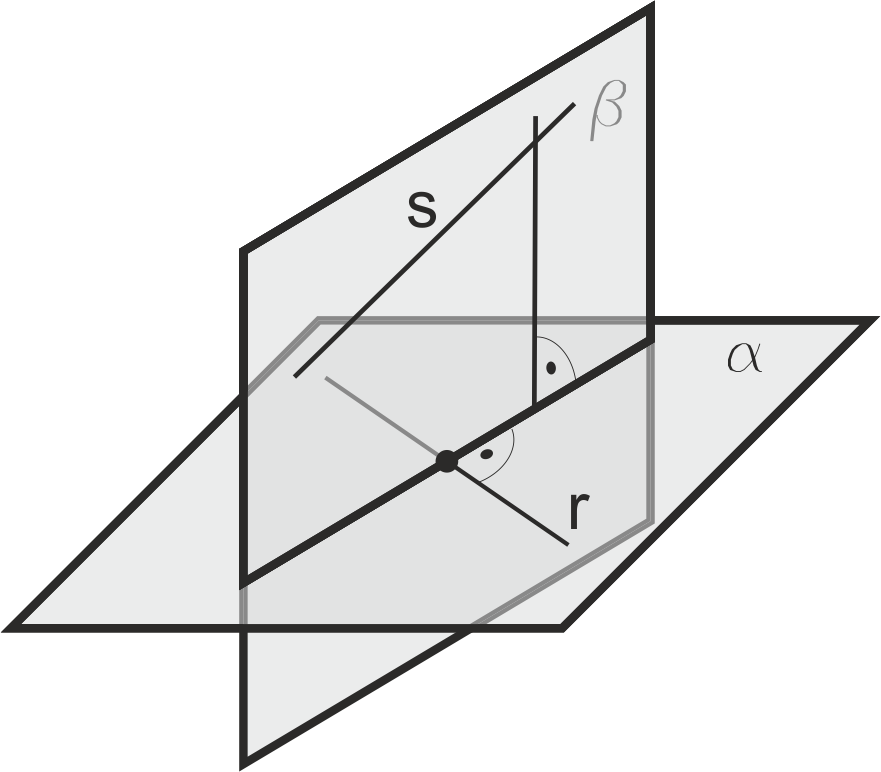
Según uno de los axiomas fundamentales, una recta paralela a un plano lo es también a una recta contenida en dicho plano. De hecho, lo es a un conjunto infinito de ellas, así que debe haber una condición adicional que defina de forma inequívoca a la recta. En este ejemplo, la recta r es paralela al plano porque también lo es a la recta s que está contenida en él.

En esta otra figura, dado el plano α por sus trazas, y el punto exterior A, supongamos que nos piden que encontremos una recta r que pasando por A sea paralela a α, y que además sea horizontal. Para encontrar-la, hemos tomado un punto cualquiera B del plano α, a partir de la horizontal del plano s. La paralela a s por A es la r buscada, ya que al ser paralela a s también es horizontal, y como s está contenida en α, r también es paralela al plano α.

Rectas perpendiculares entre sí

Dos rectas que se cortan pueden ser perpendiculares, pero esta condición de perpendicularidad no se manifiesta en ninguna de las proyecciones (salvo que el plano que las contiene sea horizontal o frontal). Para resolver problemas de perpendicularidad entre dos rectas es necesario realizar una transformación en el plano que las contiene (giro, abatimiento, cambio de plano…) para conseguir una vista auxiliar que muestre en ver-dadera proporción el ángulo que forman. Esto se verá también más adelante.

En esta figura podemos ver que las proyecciones de dos rectas perpendiculares (r y s) forman ángulos aleatorios dependiendo de la orientación del plano que las contiene.

Recta perpendicular a un plano

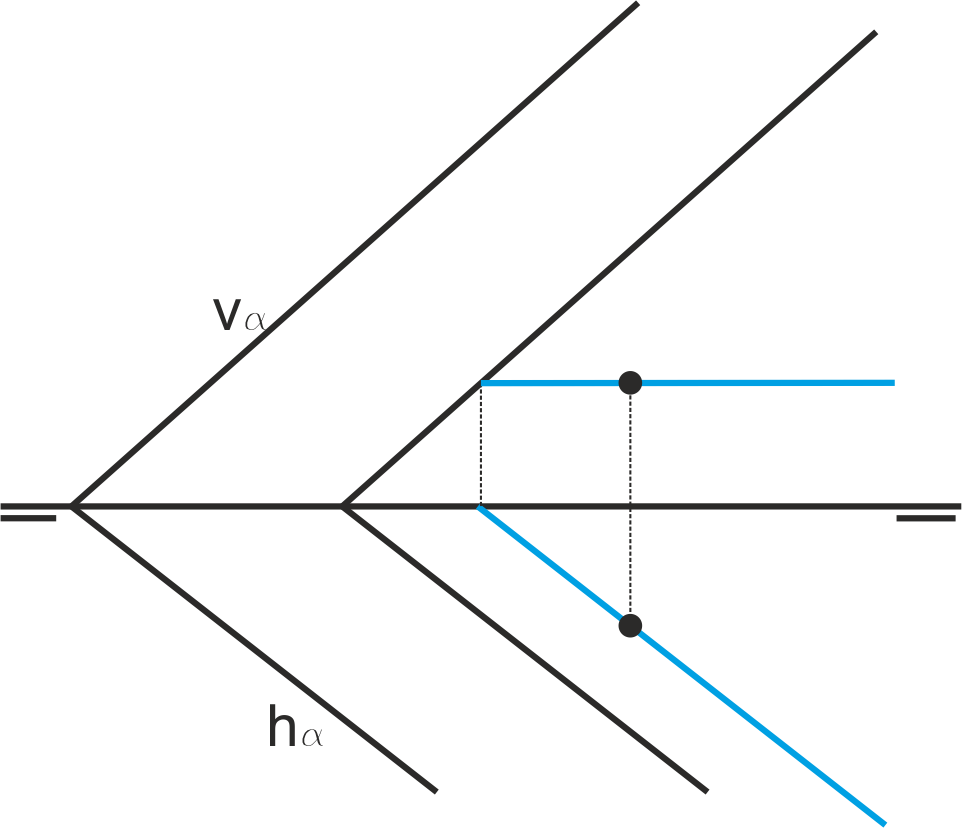
Un axioma fundamental de la geometría dice que si una recta (r, en la figura) es perpendicular a un plano, también lo es a todas las rectas del plano que pasan por el punto de corte de recta y plano (s y t en la figura).

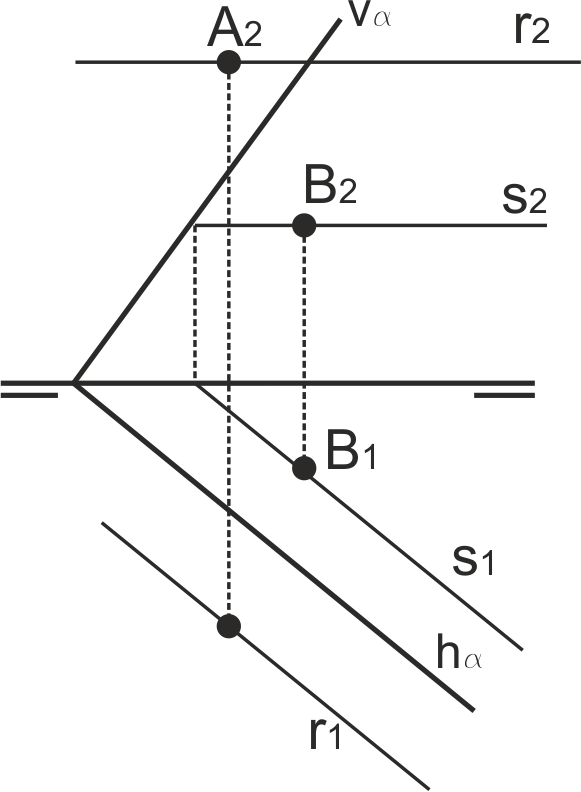
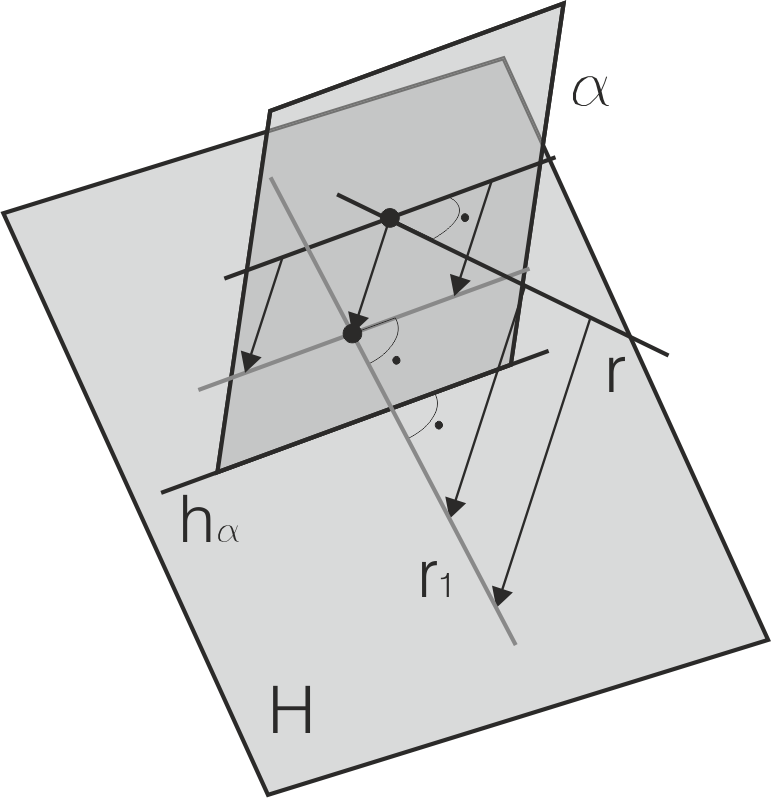
El Teorema de las tres perpendiculares extiende este axioma diciendo que si dos rectas perpendiculares (r, s) se proyectan sobre un plano paralelo a una de ellas (s), las proyecciones son perpendiculares.

Si se particulariza este Teorema considerando el plano de proyección al plano H, y el plano α perpendicular a r y que contiene a s, su traza hα también será paralela a s, por lo que la proyección de la recta r1 sobre H también será perpendicular a hα.

Como conclusión, en el sistema diédrico, las proyecciones de una recta perpendicular a un plano son a su vez perpendiculares a las trazas del plano (la proyección horizontal es perpendicular a la traza horizontal y la proyección vertical lo es a la traza vertical). En esta figura, r es perpendicular a α:

Recta perpendicular a otra por un punto exterior

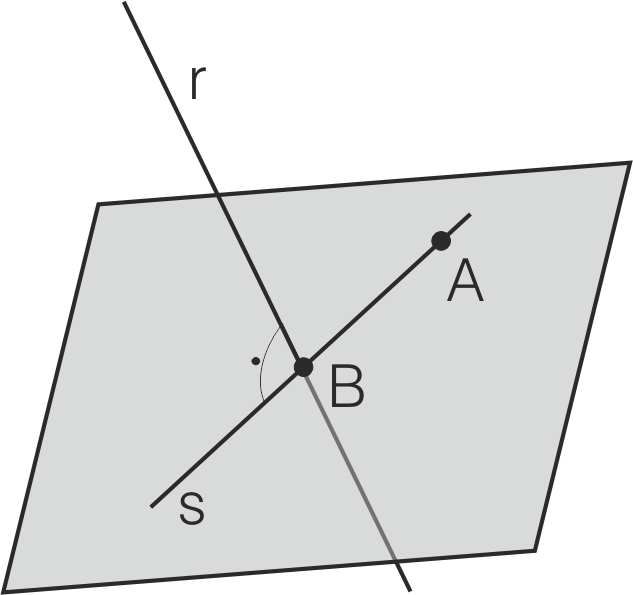
Para encontrar una recta perpendicular s a otra r por un punto exterior A, seguimos estos pasos:

• Encontramos un plano perpendicular a r que contenga al punto A (ver apartado anterior).
• Encontramos el punto B intersección de la recta r con el plano a (la intersección entre recta y plano se explica en el siguiente capítulo).
• La recta AB es la s, perpendicular a r, buscada.

Planos perpendiculares entre sí

Dos planos α y β son perpendiculares entre sí cuando uno de ellos (α en la figura) contiene al menos una recta (r) perpendicular al otro.

Para encontrar un plano β perpendicular a otro α tal que pase por una recta s, basta con trazas una perpendicular a α por cualquier punto de la recta s. Esa perpendicular y la propia recta s definen al plano β.