Introducción

Igual que ocurre con las distancias, los ángulos que forman dos entidades en el espacio no se reflejan en verdadera magnitud en las proyecciones diédricas, a no ser que el plano que contiene el ángulo sea horizontal o frontal.

Como regla general, para deducir el ángulo que forman dos entidades (rectas, planos) en el espacio, se debe mover el plano en el que está situado el ángulo buscado hasta colocarlo en posición horizontal o frontal, para así poder medir este ángulo en verdadera magnitud. Este movimiento puede realizarse mediante un abatimiento, un giro o un cambio de plano.

Ángulo de dos rectas que se cortan

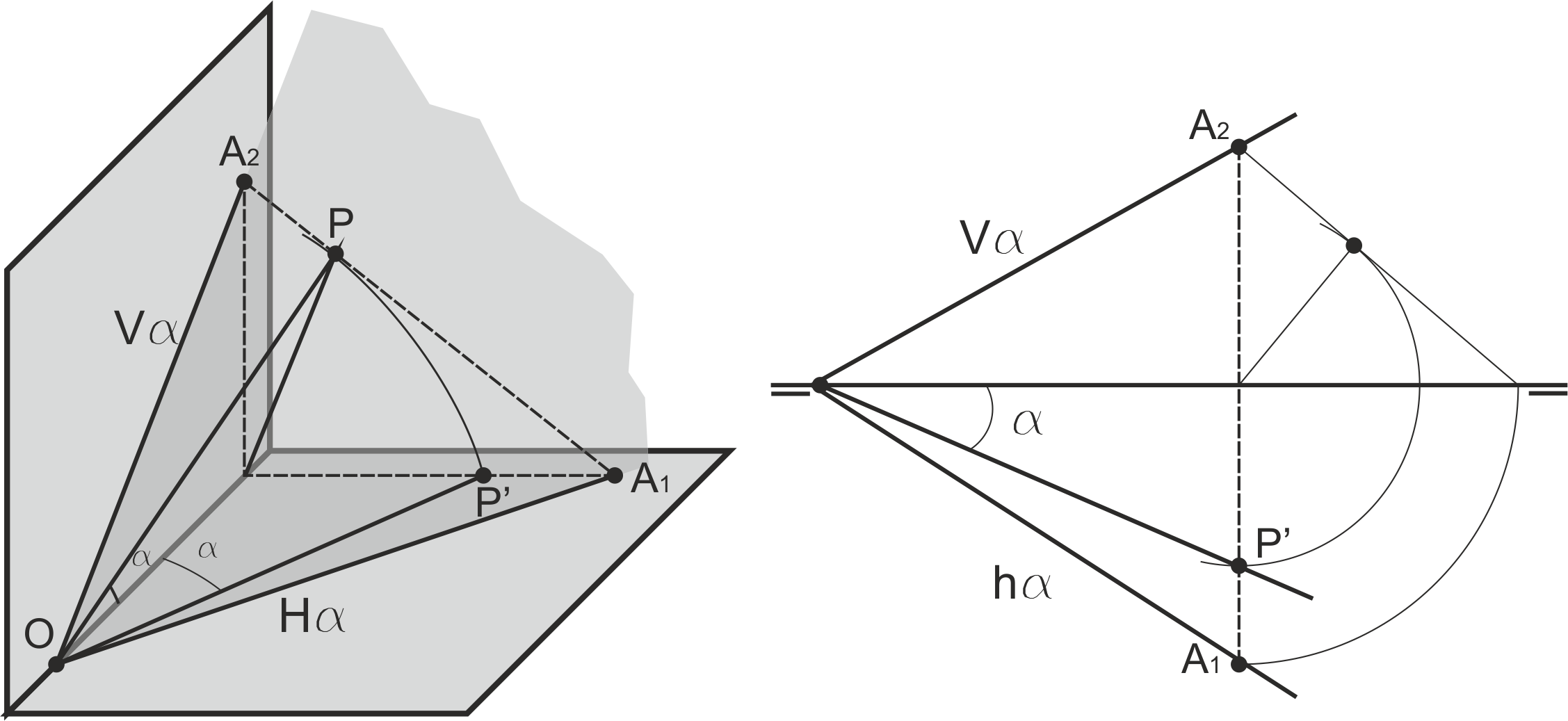
En el caso del ángulo que forman dos rectas que se cortan, se abate el plano que las contiene, el punto de corte y después se abaten las propias rectas. En este caso es muy cómodo aplicar la relación de afinidad que cumplen la proyección horizontal y la figura abatida para el trazado.

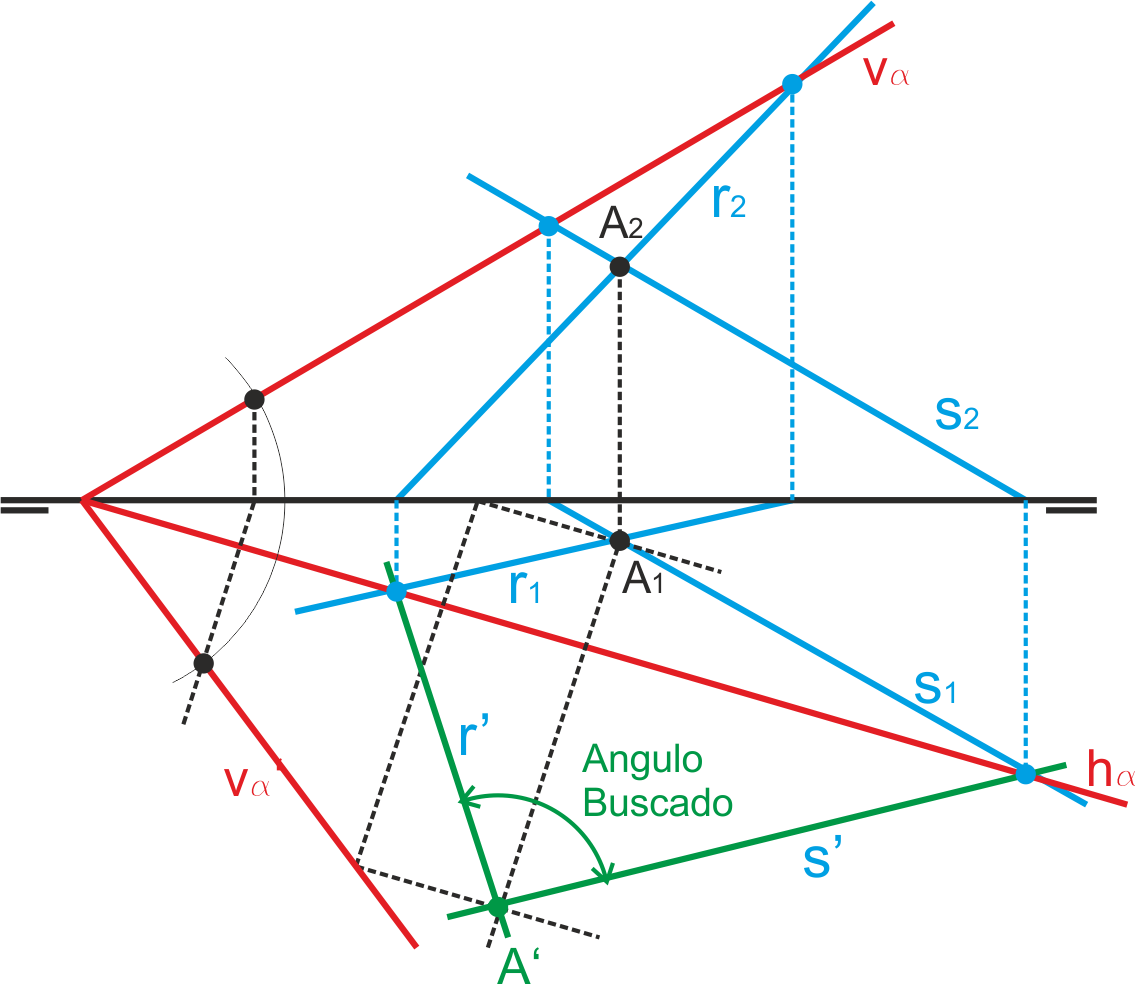
Ángulo de dos rectas que se cruzan

Resolver el ángulo entre dos rectas que se cruzan en el espacio consiste en trazar una paralela a una ellas que corte a la otra. El ángulo de estas dos rectas que se cortan es el buscado.

En general, todos los problemas de resolución de ángulos deben reducirse al cálculo del ángulo que forman dos rectas, así que habrá que dar los pasos previos necesarios para conseguir ese ángulo entre dos rectas.

Ángulo entre recta y plano

El ángulo que forman un plano α y una recta r que lo corta en el punto M es el que forman esa recta y su proyección ortogonal sobre el plano.

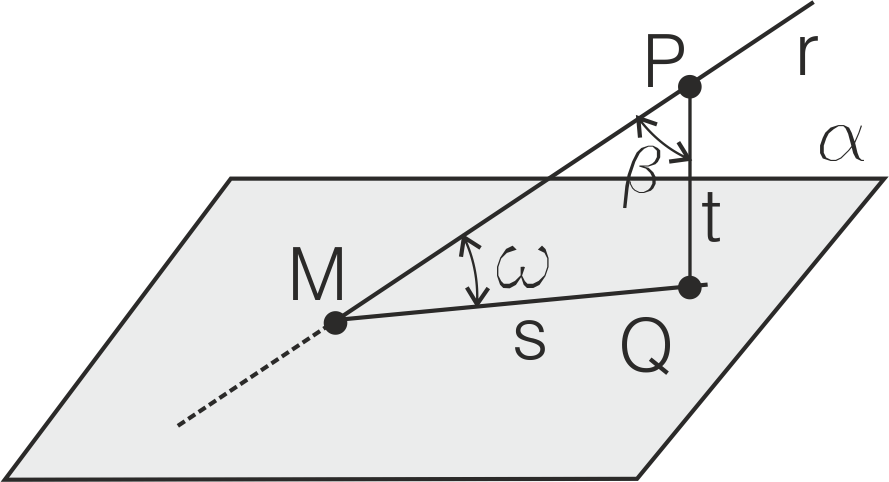
Para determinarlo, seguimos este procedimiento:

Se traza desde un punto P elegido de la recta una perpendicular t al plano α, de forma que el ángulo entre r y t cumple que es complementario del buscado (suman 90º), así que hemos reducido el problema a un ángulo entre dos rectas (r y t). Este método no proporciona el ángulo directamente, sino su complementario (β).

Si además se encuentra el punto M (corte de r con α) y el punto Q (corte de t con α), podemos obtener la recta s. Las rectas s y r determinan el ángulo buscado.

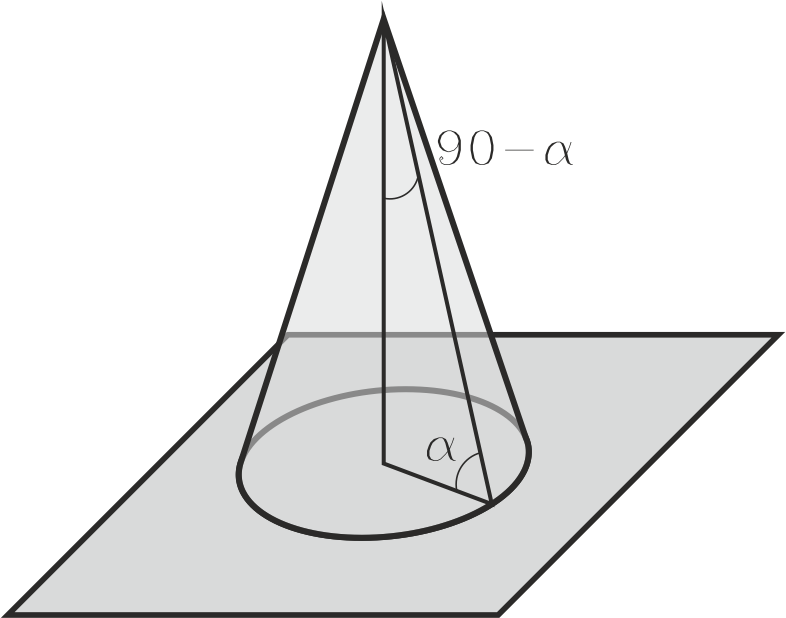
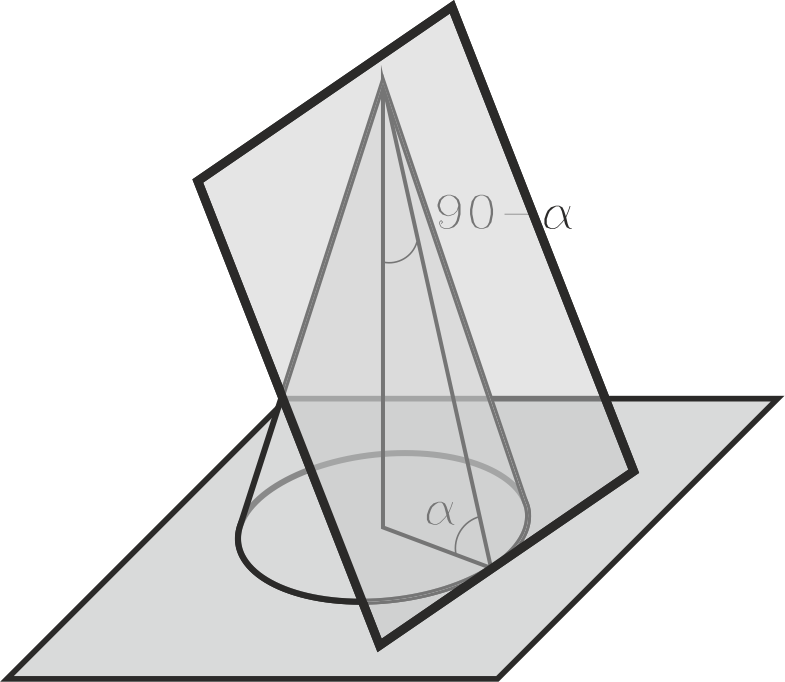
El conjunto de las rectas que forman un ángulo α determinado con un plano y pasan por un punto exterior a él es un cono de revolución apoyado en dicho plano cuyo semi ángulo cónico es el complementario de éste (90- α).

Ángulo que forman dos planos

Para determinar el ángulo que forman dos planos α y β procedemos de esta forma (ver figura):

Trazamos la línea u, intersección de ambos planos. Por un punto de ella se dibuja un plano perpendicular γ que será a su vez perpendicular a los dos planos α y β. El corte de γ con α es la recta r y el corte de γ con β es la recta s. El ángulo entre r y s es el buscado.

Hay una segunda forma: podemos es trazar dos líneas m y n, la primera perpendicular a α y la segunda, que debe cortarse con la primera, a β. El ángulo que forman m y n es el suplementario del buscado (180º menos el buscado).

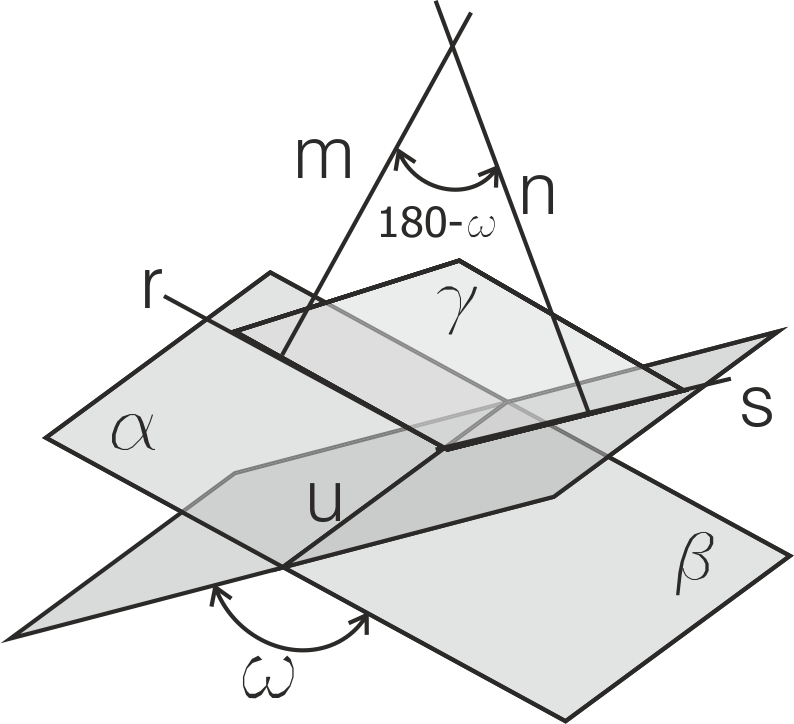
Los planos que forman un ángulo α con otro son todos tangentes a un cono de revolución apoyado en dicho plano cuyo semi ángulo cónico es el complementario (90- α) del ángulo anterior.

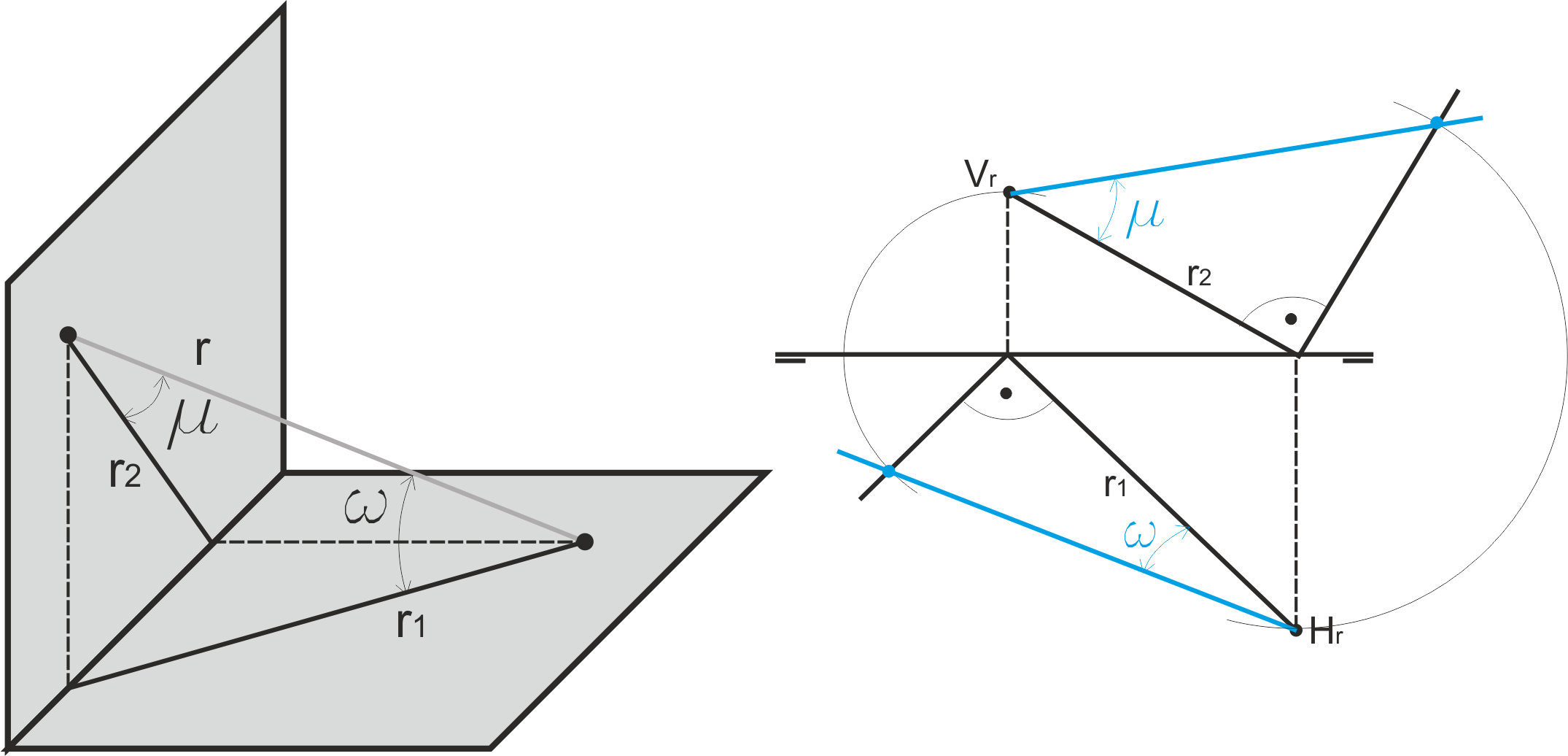
Ángulos de una recta con los planos de proyección

Para determinar los ángulos que forma una recta con los planos de proyección, se hace la construcción siguiente, basada en abatir la recta tal y como se hacía para determinar la longitud de un segmento.

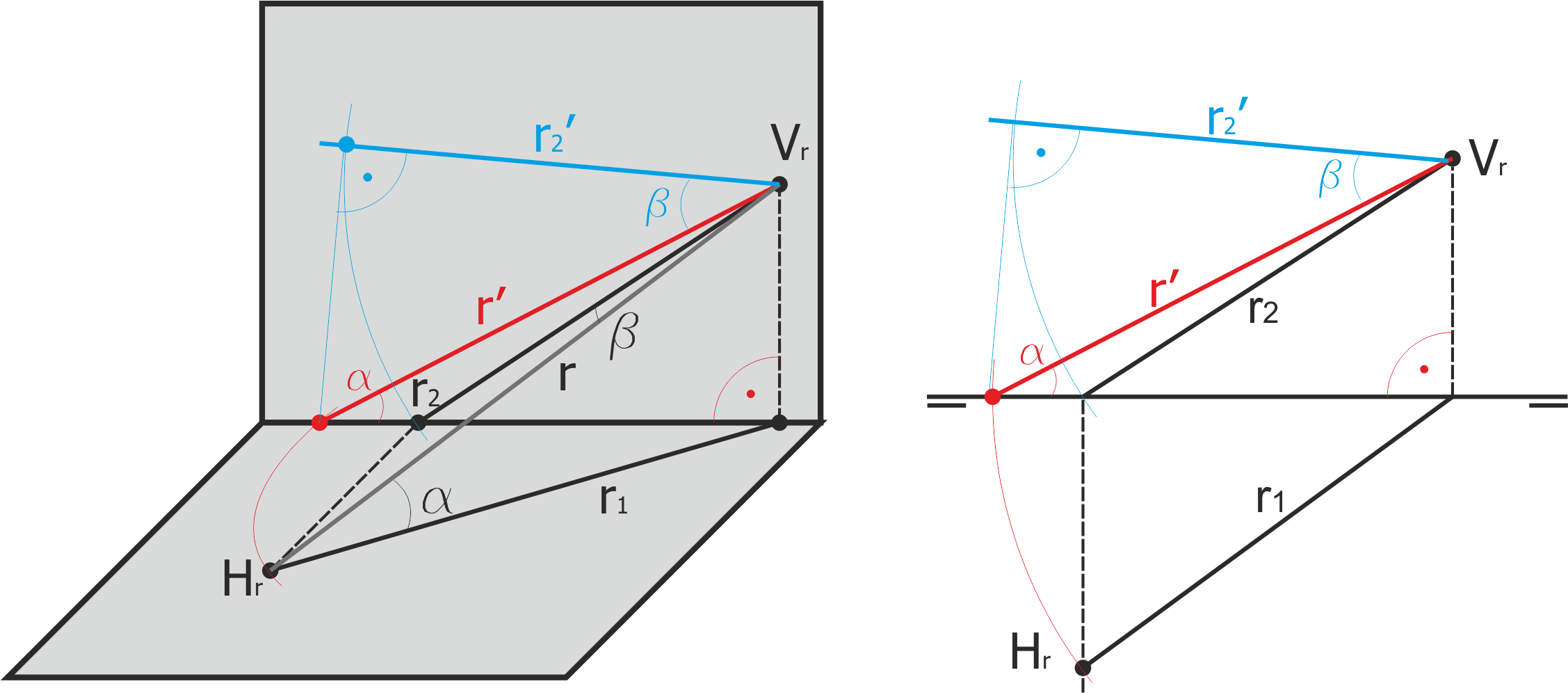
Determinación de la recta dados los ángulos que forma con H y V

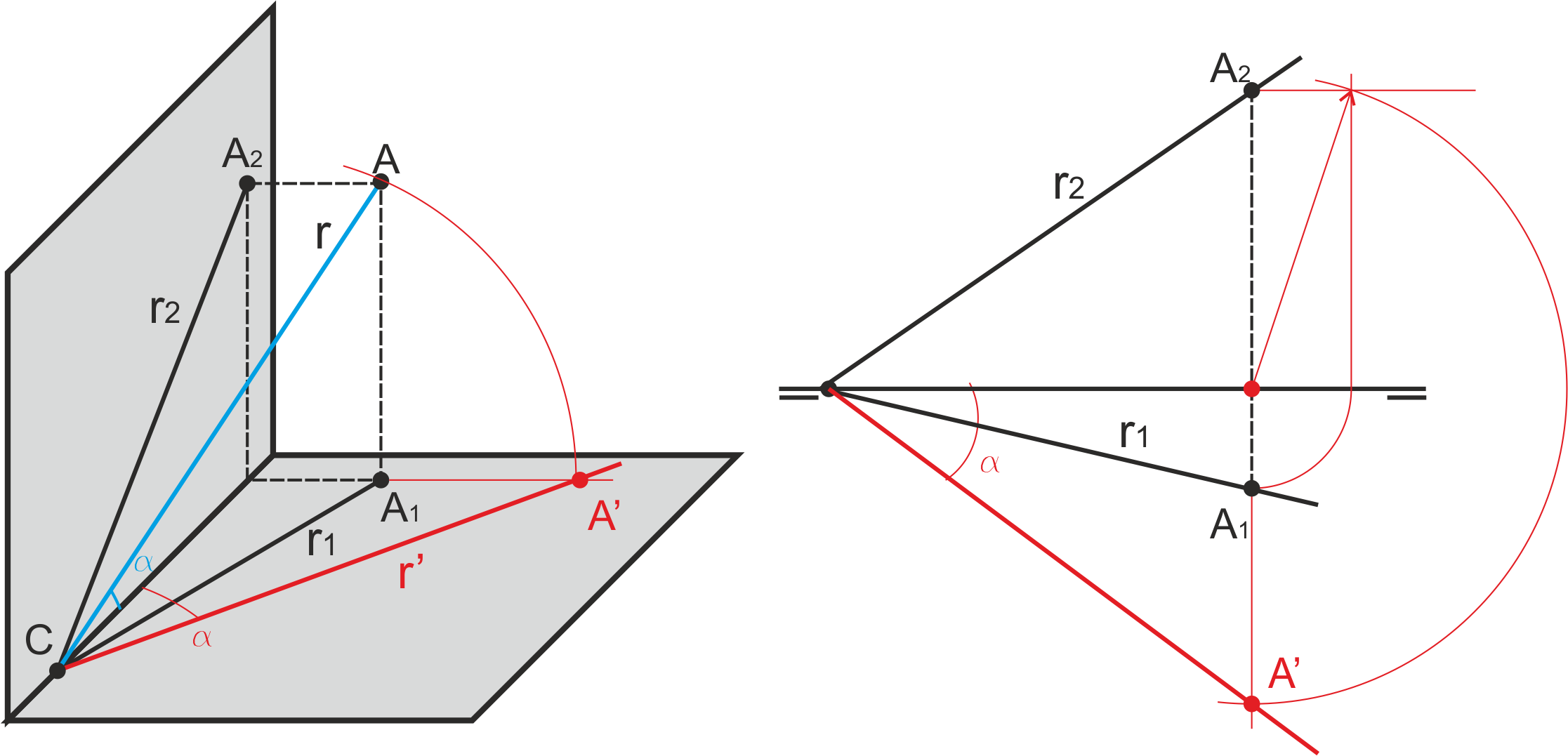
Para trazar una recta que forme ángulos α y β dados con H y V, elegimos un punto al azar como traza vertical y construimos dos triángulos rectángulos abatidos; el primero de ellos contiene el ángulo alfa y determina la longitud del segmento r. El otro, sobre el primero, contiene el ángulo beta.

Desabatiendo este último se obtiene el pie de la traza horizontal, y desabatiendo el primero se obtiene la traza horizontal (ver figura de la derecha). Para que la construcción sea correcta, α + β debe ser <= 90º. Lo contrario es geométricamente imposible.

También existe un método mucho más simple, basado en la construcción siguiente:

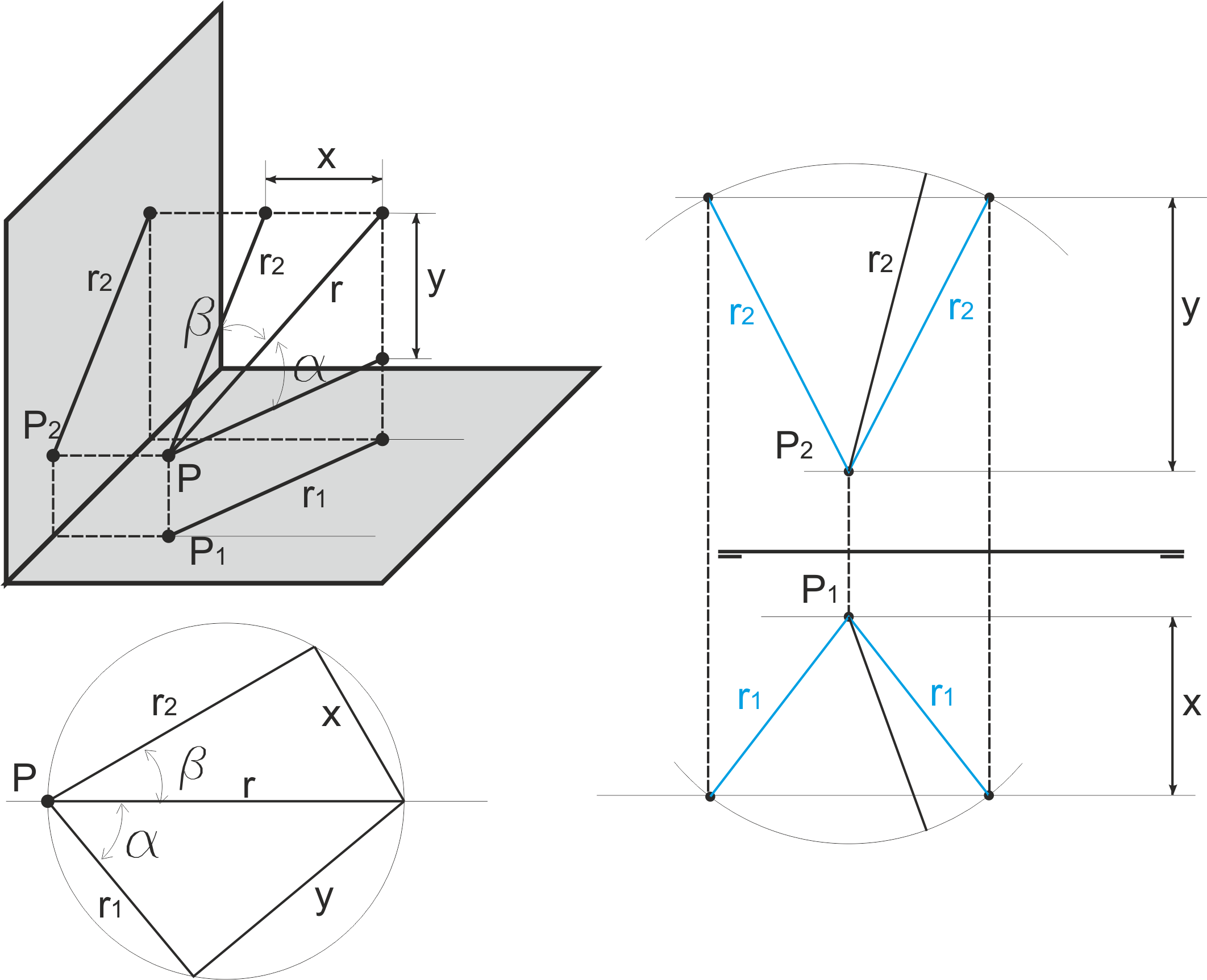
Suponemos un punto P y otro punto hipotético cualquiera trazada la recta r desde el punto P. Según la composición de la izquierda, para los ángulos de r dados α y β ese punto tendrá una diferencia de cota “y” y una diferencia de alejamiento “x”.

Eligiendo una longitud de r al azar construimos la circunferencia de abajo, que contiene dos triángulos rectángulos que nos dan las longitudes de las proyecciones r₁, r₂ y las diferencias de cota y alejamiento x e y. No tenemos más que aplicar estos datos sobre el punto P (figura de la derecha) para obtener las posibles soluciones. Cualquier combinación de r₁ y r₂ es válida, hay que elegir la que se ajuste a los condicionantes del problema.

Ángulos que forma un plano con los planos de proyección

El ángulo que forma un plano con H es el que forma una lmp (línea de máxima pendiente) del dicho plano con H, así que dibujando una lmp cualquiera del plano reducimos el problema al de un ángulo entre una recta y el plano H. Análogamente, el ángulo que forma un plano con el plano V es el que forma una lmi (línea de máxima inclinación) del plano con V, así que dibujando una lmi cualquiera reducimos el problema al de un ángulo entre una recta y el plano V.

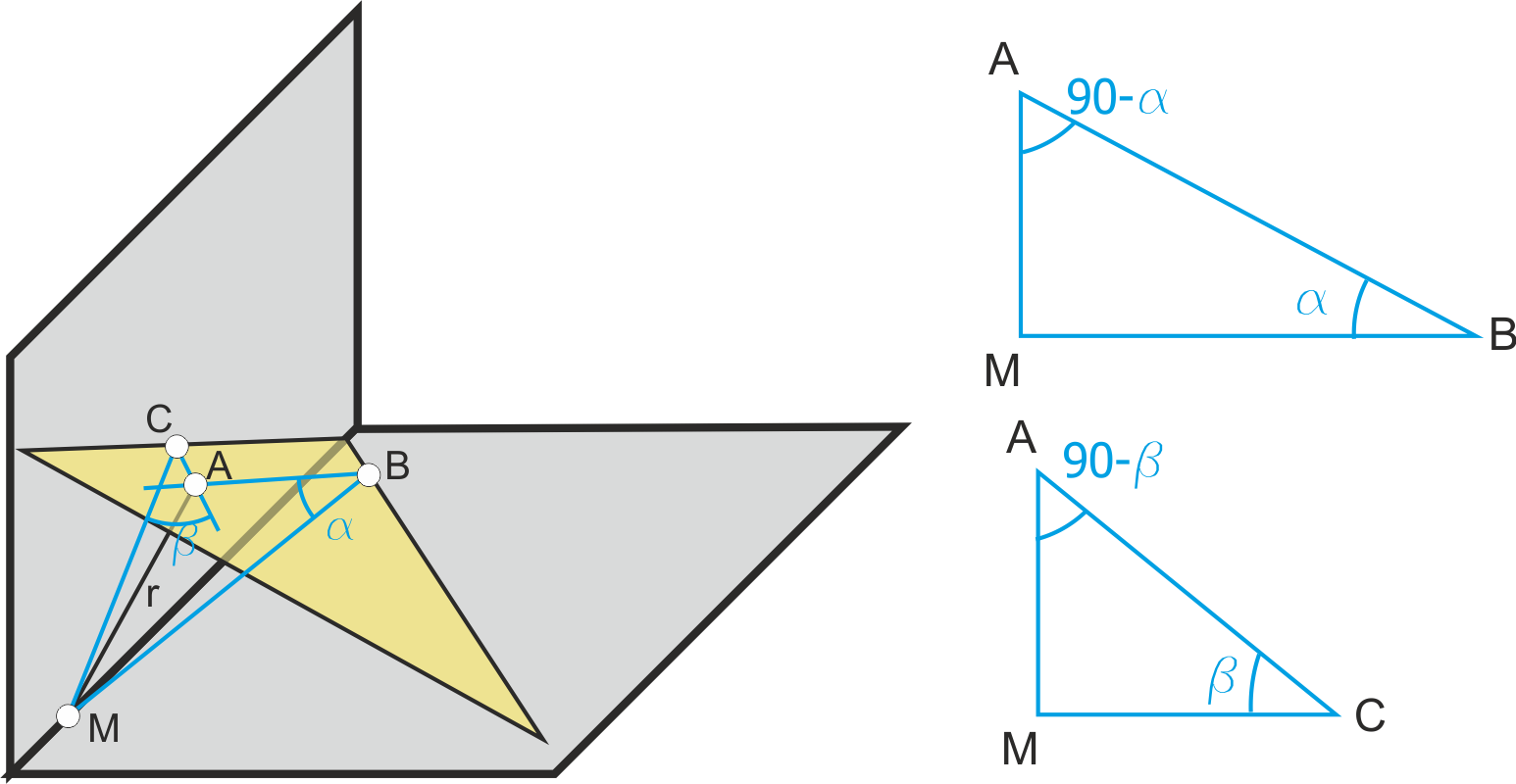
De esta forma, para dibujar un plano que forma un ángulo α con el plano H y un ángulo β con el plano V nos basamos en la construcción siguiente:

Elegimos un punto M de la línea de tierra y trazamos una recta r que forme un ángulo 90-α con H y 90-β con V. Esta recta será perpendicular al plano buscado.

En la figura, se observa que la recta r es perpendicular a una lmp y a una lmi del plano que se cortan en el mismo punto de corte de r con el plano.

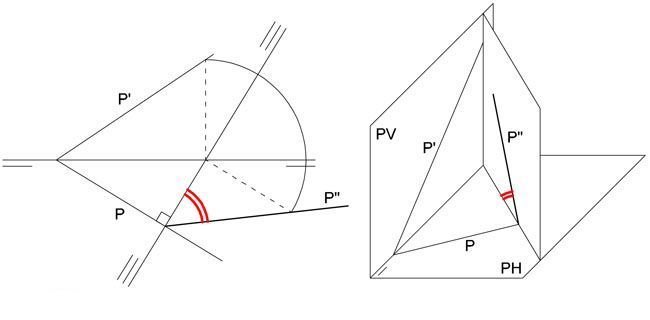
Para determinar el ángulo que forma un plano con el plano horizontal de proyección, podemos hacer un cambio de plano vertical y convertirlo en proyectante vertical, con lo cual veremos dicho ángulo en verdadera magnitud.

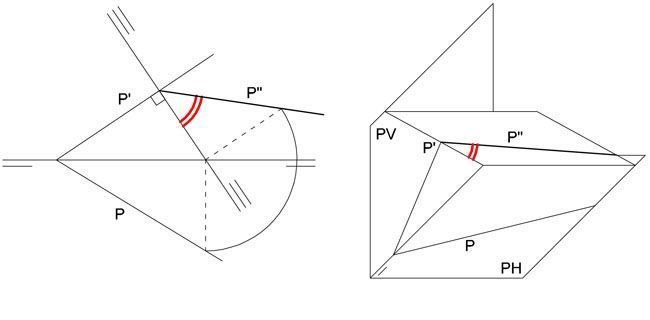
Análogamente, podemos determinar el ángulo que forma un plano con el plano vertical de proyección haciendo un cambio de plano horizontal para convertirlo en proyectante horizontal, con lo cual veremos también dicho ángulo.

Por último, debemos saber que:

• El ángulo que forma un plano con el plano horizontal de proyección es el mismo ángulo que forma cualquier recta de máxima pendiente del plano con el plano horizontal de proyección.
• El ángulo que forma un plano con el plano vertical de proyección es el mismo ángulo que forma cualquier recta de máxima inclinación del plano con el plano vertical de proyección.

Determinación del plano dados los ángulos que forma con los planos de proyección

Podemos usar el método de la recta sabiendo que los ángulos que forma un plano con los planos de proyección son los complementarios (90-a) de los que forma una recta perpendicular al plano con dichos planos de proyección. Así, podemos calcular una recta perpendicular (por el método método anterior) y a partir de ella el plano.

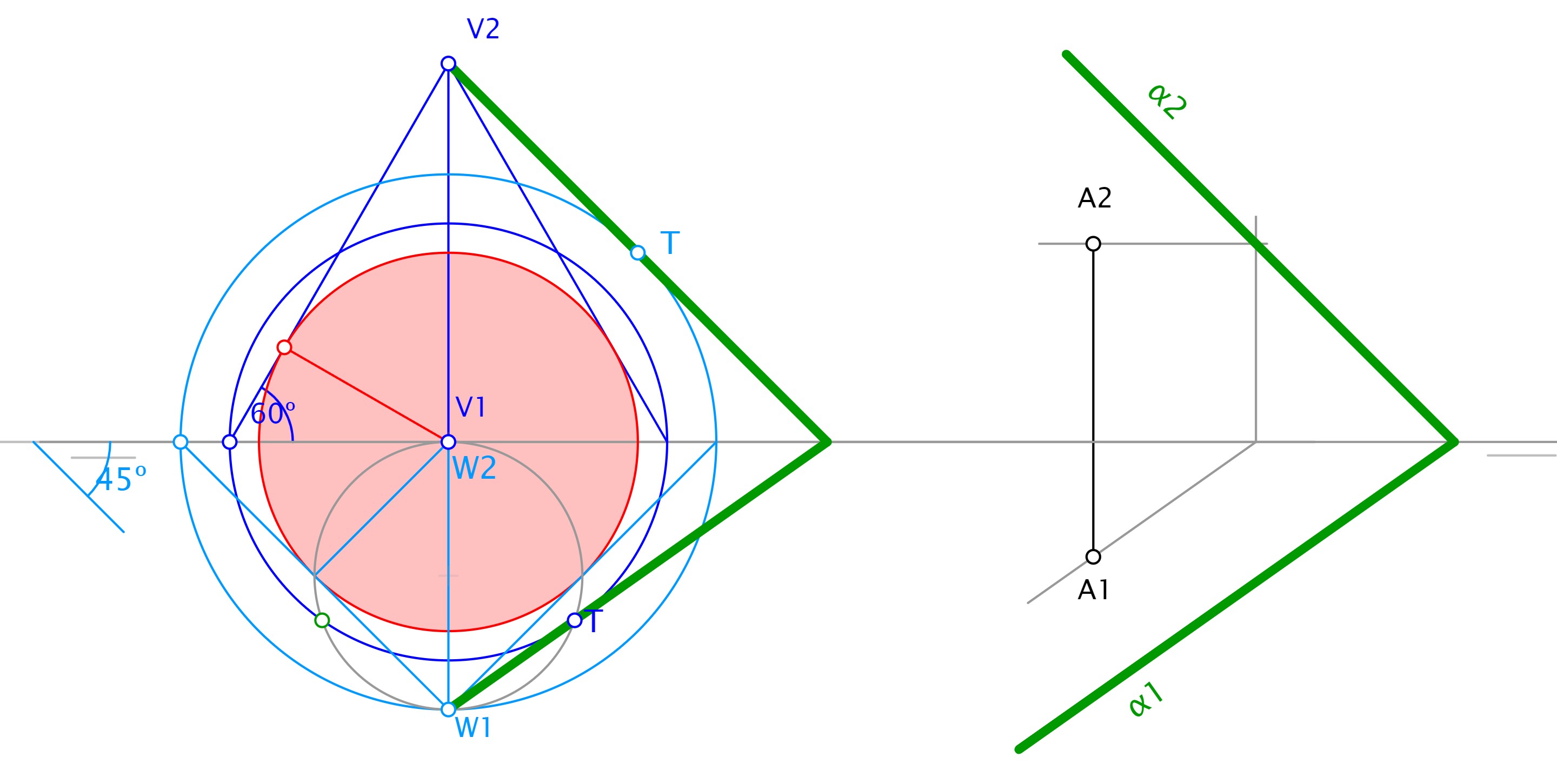
Existe un método alternativo para conseguir los mismos resultados, consistente en trazar unos conos con los ángulos cónicos dados. Si el ángulo del plano con el PHP es 60º, trazamos desde un punto V cualquiera en el PVP un cono de eje vertical cuyo ángulo sea 60º (el plano será tangente a ese cono, asi que su traza horizontal será tangente a su base), y dibujamos una esfera tangente a él con centro en V1. luego hacemos un segundo cono de eje de punta y vértice W con el otro ángulo (45º en la figura) que también sea tangente a la esfera. Como el plano también será tangente a él, la traza vertical del mismo será tangente a la base del cono. Como sabemos que las trazas del plano pasan por W1 y V2, basta lanzar esas tangentes, lo que nos dará las direcciones de las trazas del plano. Hay 4 soluciones posibles (solo se ha representado una).

Plano que contiene a una recta y forma un ángulo determinado con el plano horizontal o vertical de proyección

Dada la recta r, si queremos que esté contenida en un plano que forma un ángulo determinado con el plano horizontal de proyección, dibujamos por un punto A de ella un cono de eje vertical cuyo ángulo cónico sea el dado. Sabemos que el plano debe ser tangente a ese cono para que forme el mismo ángulo con el PHP, así que su traza horizontal será tangente a la base del cono (en una recta m de máxima pendiente del plano). Como además sabemos que al contener a la recta su traza horizontal pasará por la traza horizontal de la misma, ya tenemos la solución (habrá dos soluciones posibles, ya que hay dos tangentes posibles).

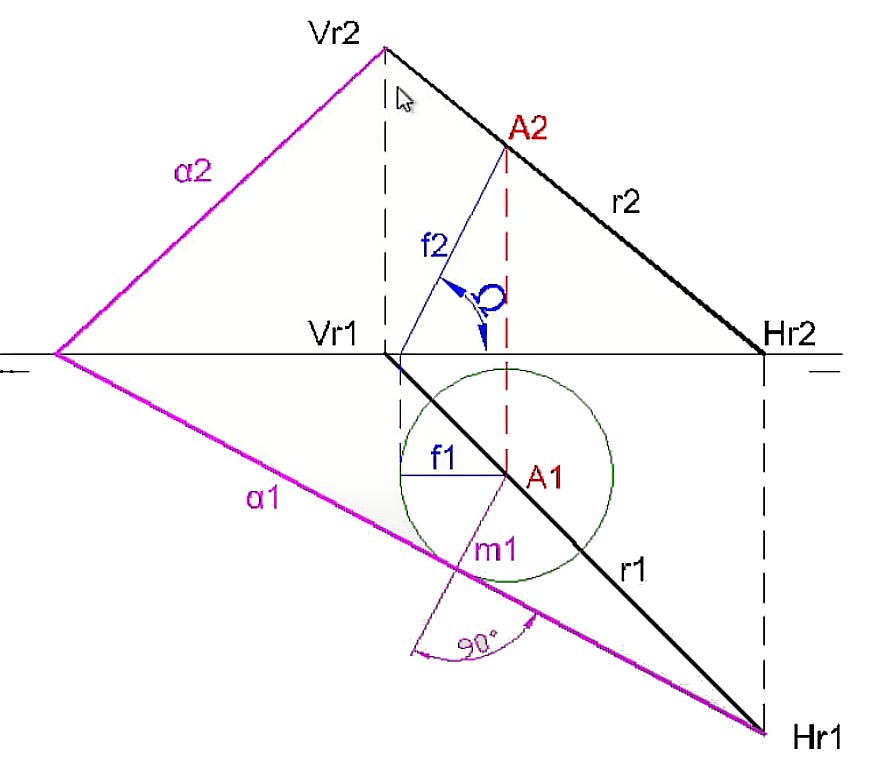
Análogamente podemos buscar el plano que conteniendo a la recta forme un ángulo dado con el PVP, usando un cono de eje de punta y base en el PVP.

Ángulos de una recta con la línea de tierra

El ángulo que forma una recta con la línea de tierra puede determinarse abatiendo la recta alrededor de ella hasta uno de los planos de proyección (el H en la figura).

Ángulo de un plano con la línea de tierra

Para determinar el ángulo que forma un plano con la LT se elige un punto M de la LT y se traza por él la perpendicular al plano. El punto de corte resultante, unido con el vértice del plano, determina una recta (AB en la figura de la derecha) que forma con la LT el ángulo buscado, con lo que el problema se reduce al caso que acaba de presentarse.

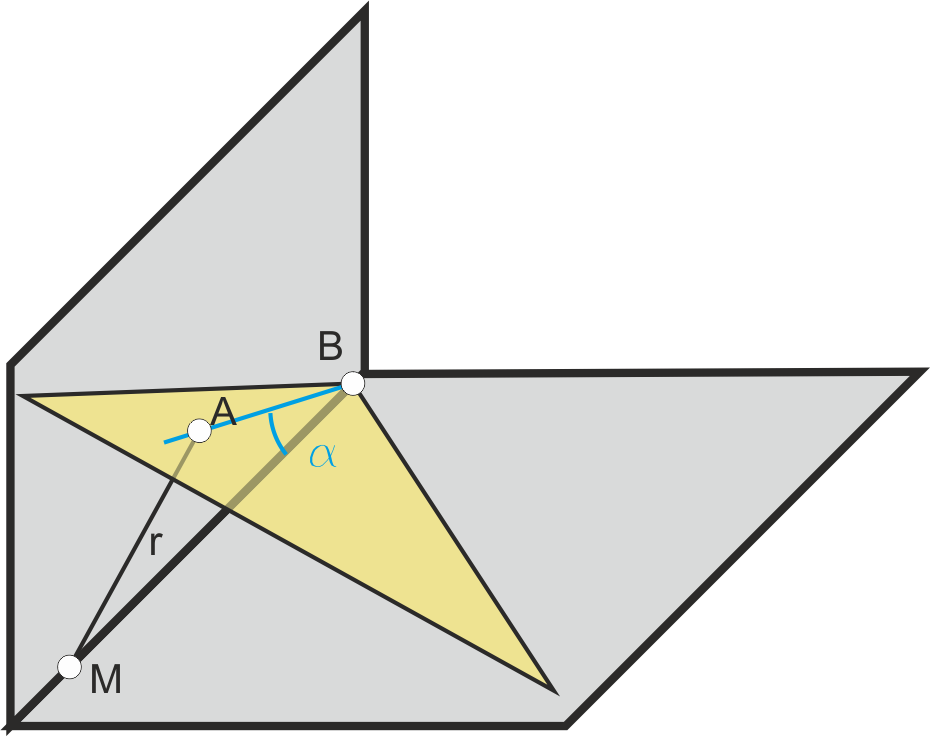
Existe otra construcción, más simple, que consiste en tomar una recta de perfil del plano, y en ella elegir el punto más cercano a la LT (P en la figura). Abatiendo la recta que va desde el vértice del plano hasta ese punto tenemos el ángulo buscado.