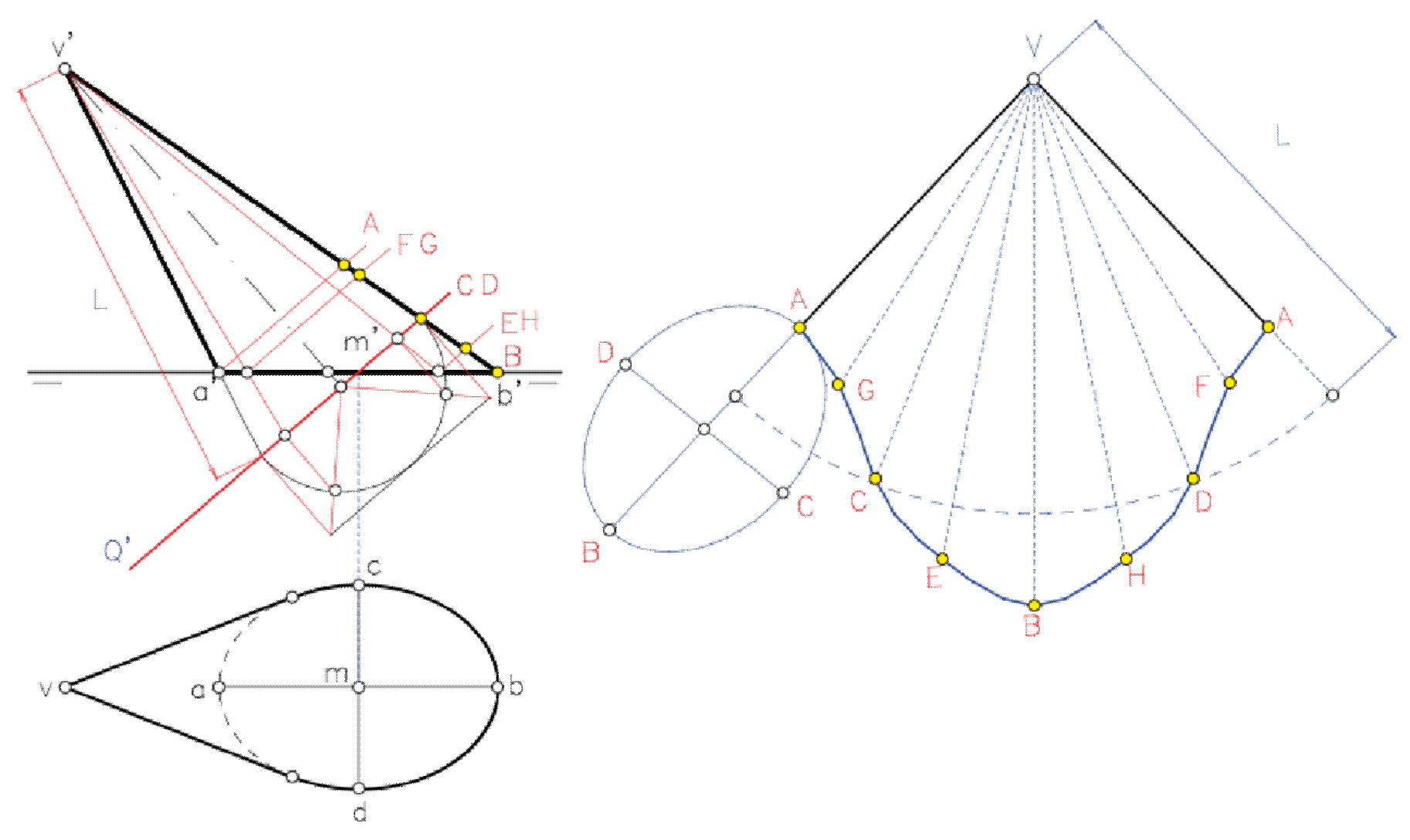
Descripción y elementos

Una superficie cónica es la engendrada por una recta que se mueve alrededor de otra con la que se corta. Esta última, la fija, se denomina eje, y la que se mueve – y sus diferentes posiciones – se denominan generatrices (g). El vértice del cono (V) es el punto de corte del eje con las generatrices.

Si el movimiento de la generatriz es circular (giro), entonces el cono es de revolución.

Cuando se corta una superficie cónica de revolución por un plano (sección plana), la intersección obtenida es una curva cónica. Dependiendo de la posición relativa del plano con respecto al eje de la superficie cónica (el ángulo que forma con el eje), se obtendrá una de estas curvas planas: Elipse, Parábola, Hipérbola (ver el capítulo dedicado a las cónicas).

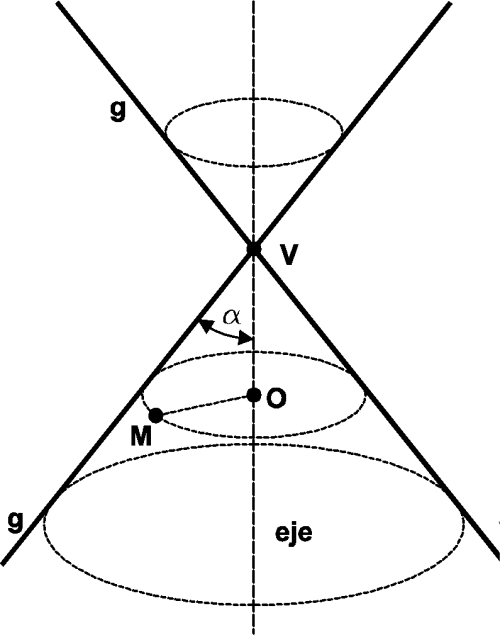
Las curvas cónicas son curvas de segundo grado. Esto quiere decir que cualquier recta que las corte lo hace en un máximo de dos puntos.

En Geometría Descriptiva, nos solemos referir a un cono como la superficie cónica delimitada por el vértice (esto es, una sola rama) y una sección plana que le produce un plano que lo corta. Esta intersección es la llamada base del cono.

La altura de un cono se define como la distancia, medida sobre una perpendicular, entre el vértice y la base.

Si el cono es de revolución, y el plano de la base es perpendicular a su eje, el cono se denomina recto, y la base es un círculo. Si el plano de la base no es perpendicular, la base es una curva cónica (si es un cono de superficie finita, será una elipse).

Se denomina cono truncado a aquel que está delimitado por dos planos (paralelos o no).

Generatrices de contorno

En los conos, como en cualquier figura con superficies curvas, no proyectamos toda la superficie, sino únicamente su contorno. De forma particular, el contorno de un cono estará formado por las proyecciones de su base (que se regirán por los métodos vistos hasta ahora, basados en la proyección de ejes o diámetros conjugados), y por las proyecciones de las dos generatrices más exteriores, esto es, las llamadas generatrices aparentes, de borde o de contorno.

Hay que tener en cuenta que en las dos proyecciones diédricas las generatrices aparentes no se corresponden, esto es, las proyecciones de las rectas que representan las generatrices aparentes en una proyección no se corresponden con las de la otra proyección, y viceversa.

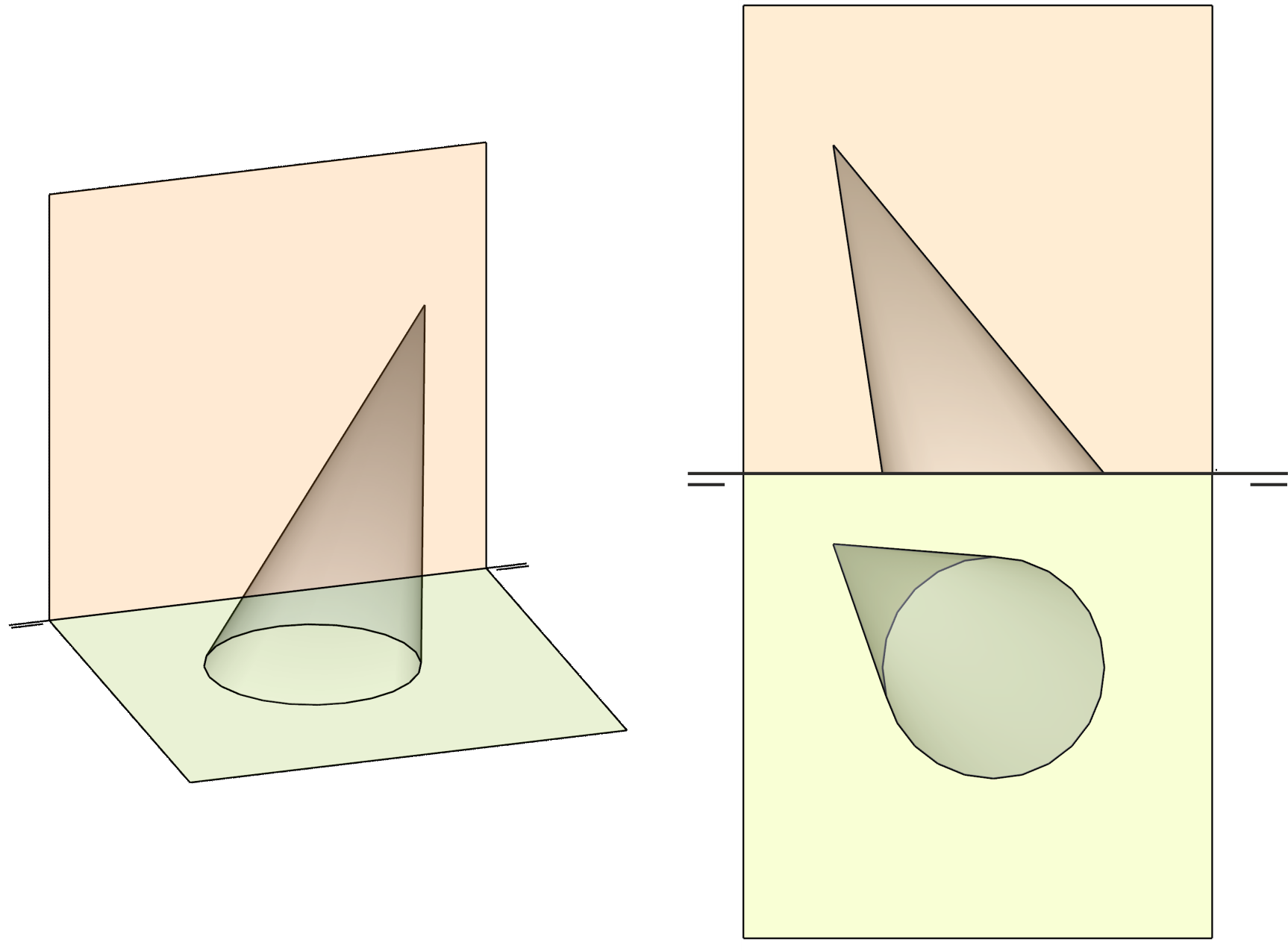
Pertenencia de un punto a un cono

Para determinar si un punto pertenece a un cono, debemos comprobar que pertenece a una de sus generatrices. Para trazarla, debemos buscar el punto de la base del cono desde la cual parte.

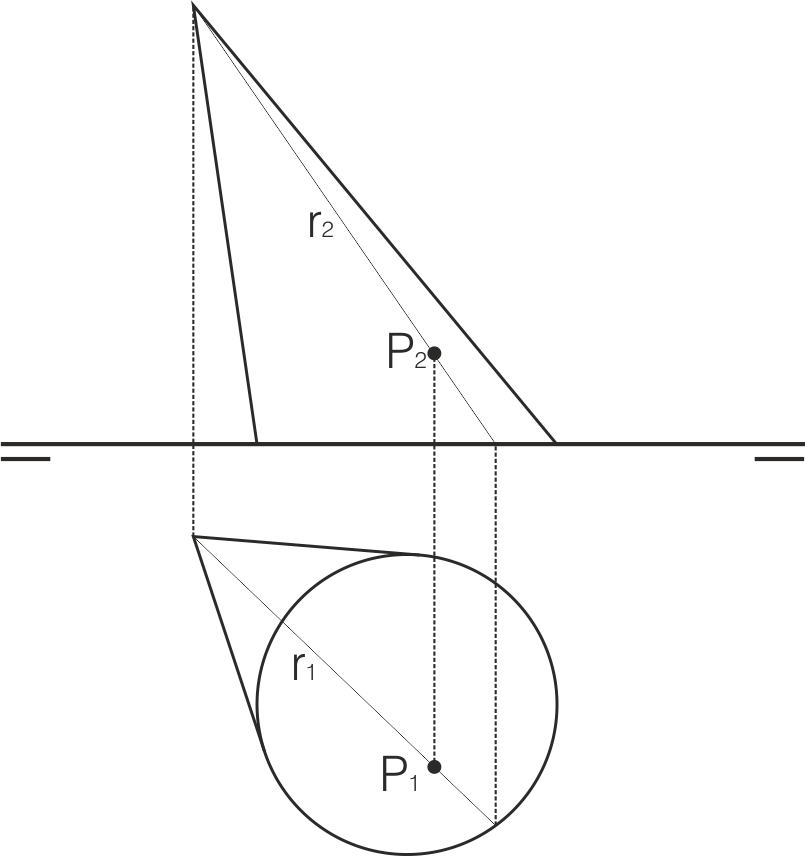
Determinación de la sección plana y/o base de un cono

La sección recta de un cono de revolución es, naturalmente, una circunferencia.

En el espacio, para determinar los elementos de la sección oblicua de un cono de revolución (aplicable también en el caso de la base de un cono oblicuo), puede usarse el Teorema de Dandelin (ver capítulo correspondiente a las cónicas).

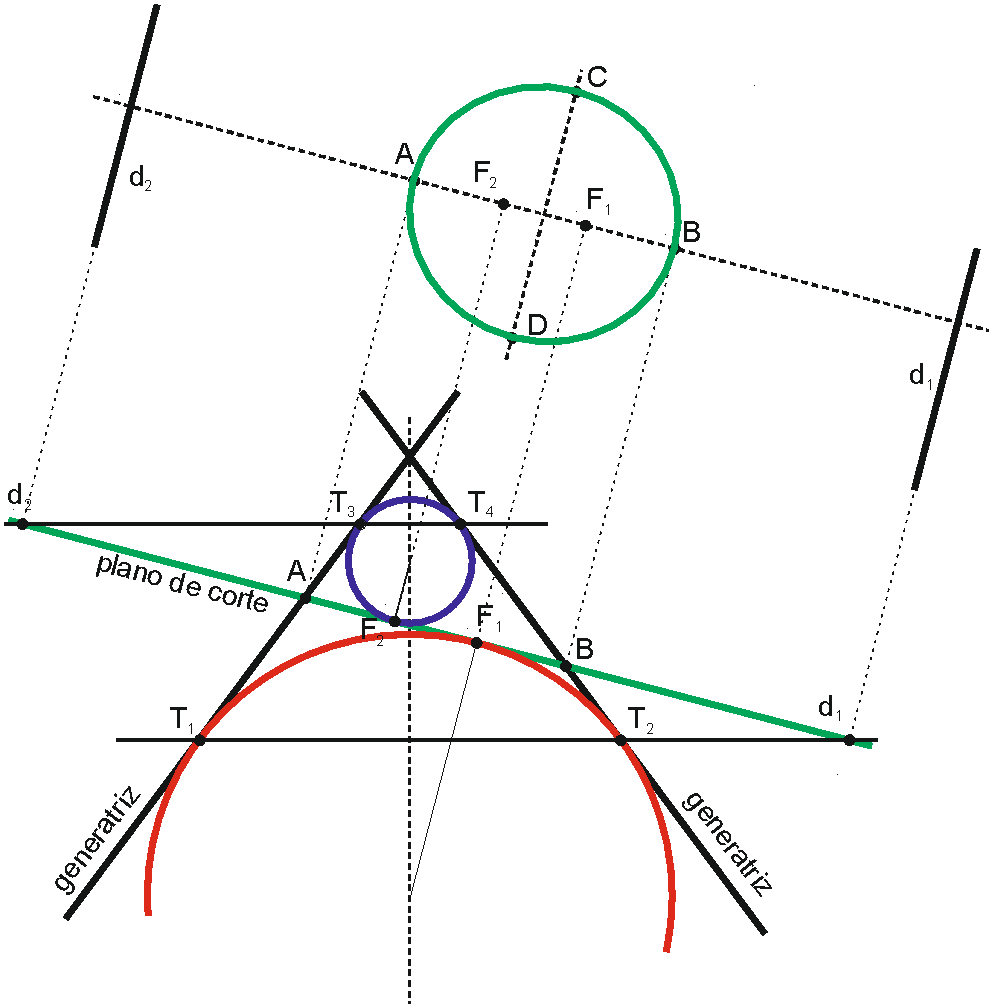
En el caso de que el cono tenga superficie finita y la sección plana (o base) sea una elipse, y su eje sea vertical o frontal, hay un método simplificado que permite obtener sus ejes.

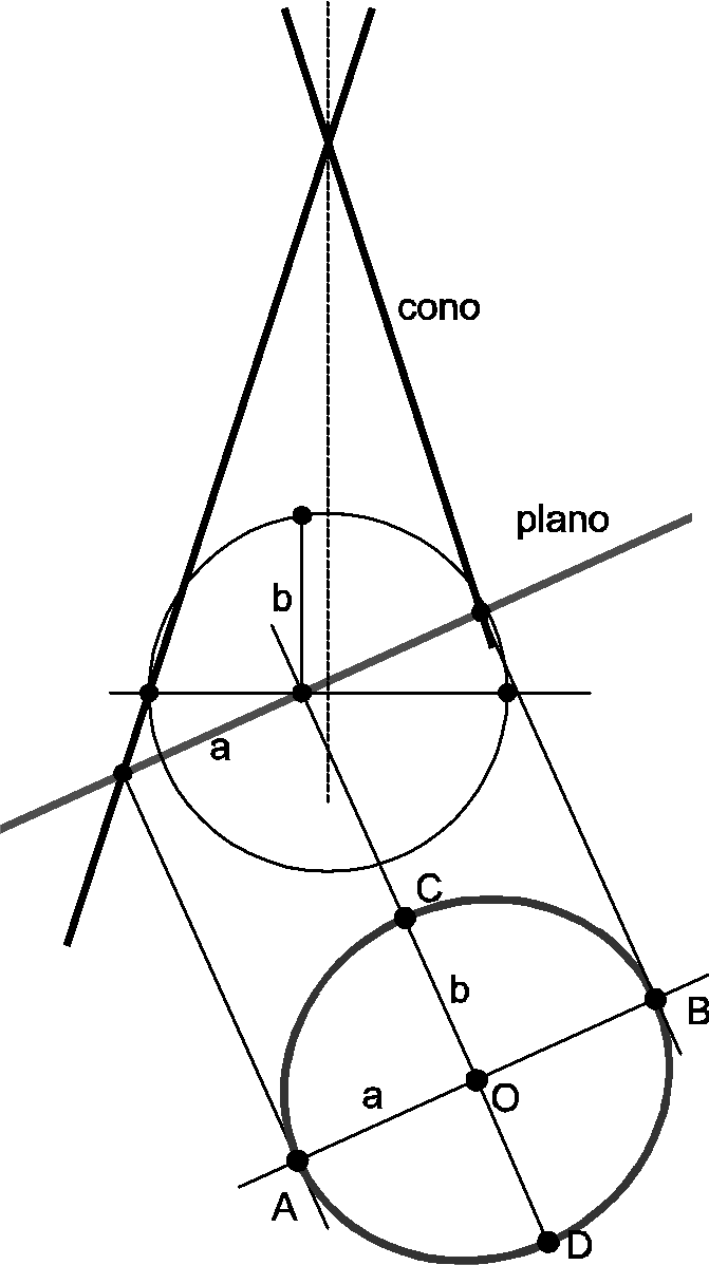
Una vez encontrada la base, las generatrices aparentes en las proyecciones que correspondan son las tangentes exteriores a la elipse, y para trazarlas habría que usar el método geométrico correspondiente (ver capítulo dedicado a la elipse).

Como caso genérico, podemos encontrar la intersección del cono con cualquier plano (el resultado es una curva cónica) cortando el plano con algunas generatrices del cono elegidas convenientemente.

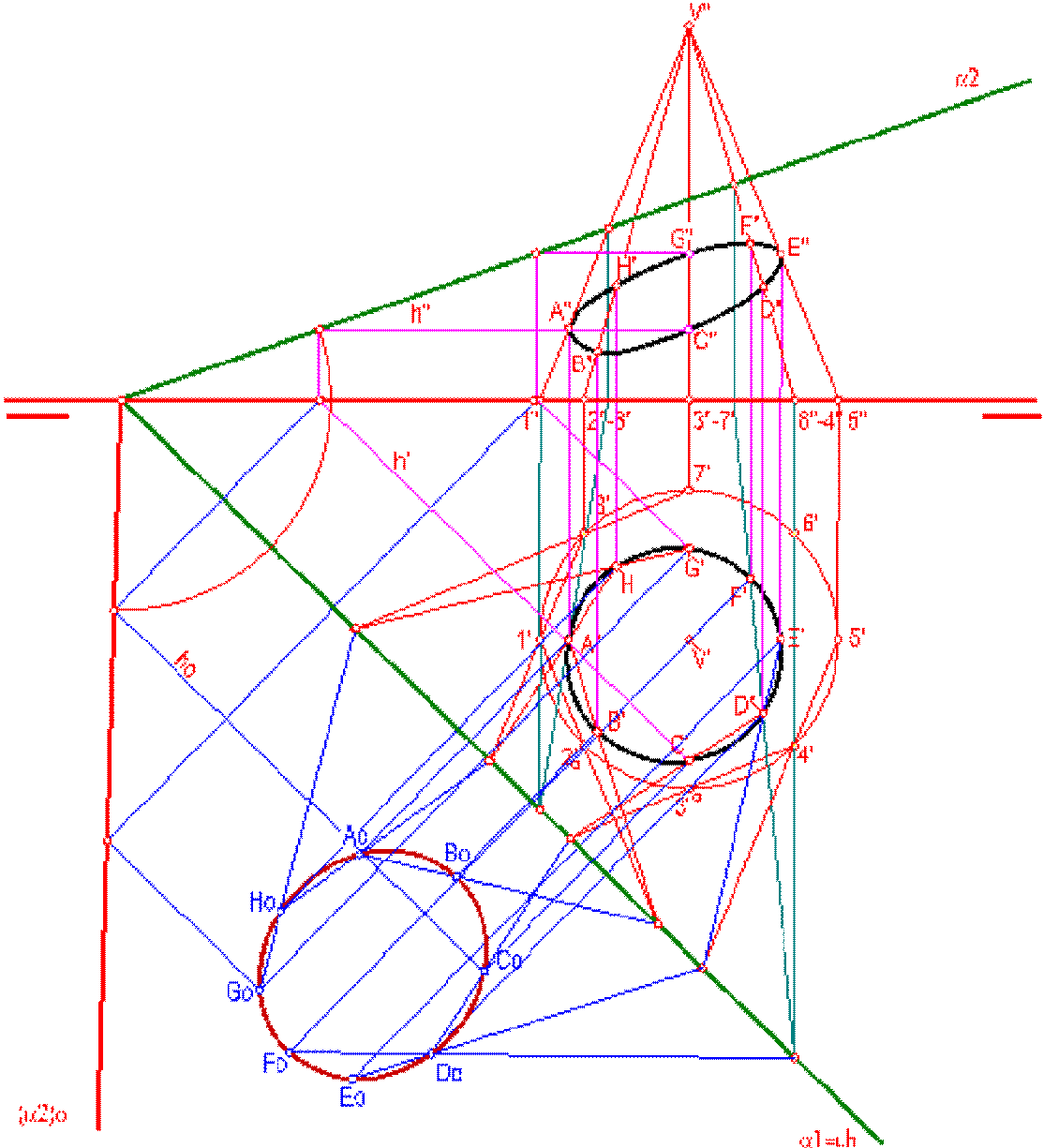
Puede comprobarse que, al igual que ocurría en la pirámide, existe una relación de homología entre la proyección horizontal de la base y la sección, en la cual el centro es la proyección horizontal del vértice, y el eje es la traza horizontal del plano de corte.

También, como en todas las figuras planas abatidas, existe una afinidad que relaciona la proyección horizontal de la sección con la sección abatida, en la cual el eje es la traza horizontal del plano y la direccion la perpendicular a ella.

Si la pirámide es recta y de revolución también podemos usar como elementos auxiliares para calcular el corte círculos horizontales del contorno del cono, e irlos cortando con el plano (mediante planos auxiliares horizontales).

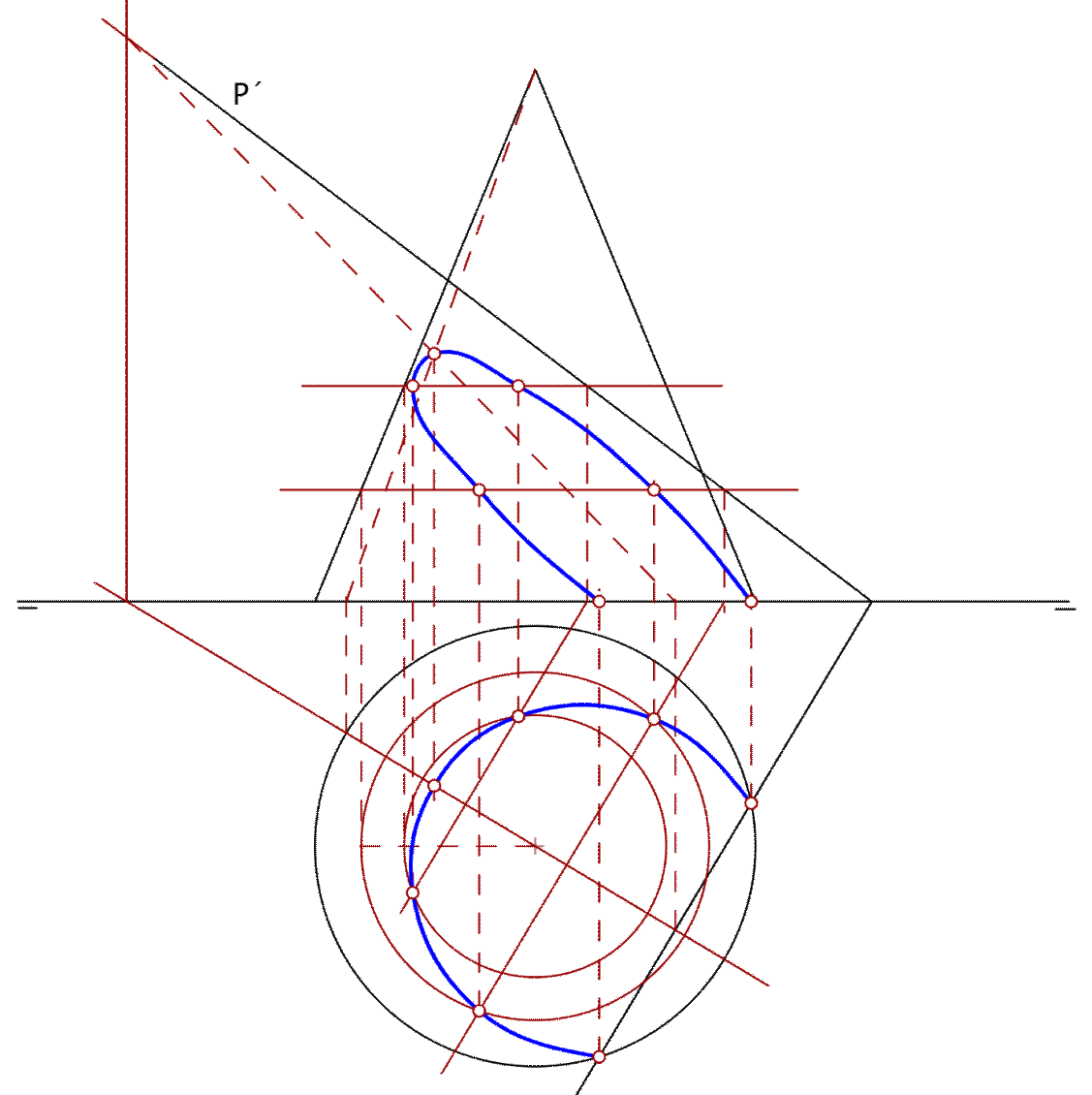
Si el plano secante no es proyectante, lo más interesante es realizar un cambio de plano para colocarlo en posición conveniente (proyectante), y reducir el problema del corte al caso anterior. El cambio de plano debe hacerse colocando la nueva línea de tierra perpendicular a la traza invariante del plano (en este caso la horizontal) pero de forma que la nueva proyección (vertical) quede en una zona libre del dibujo.

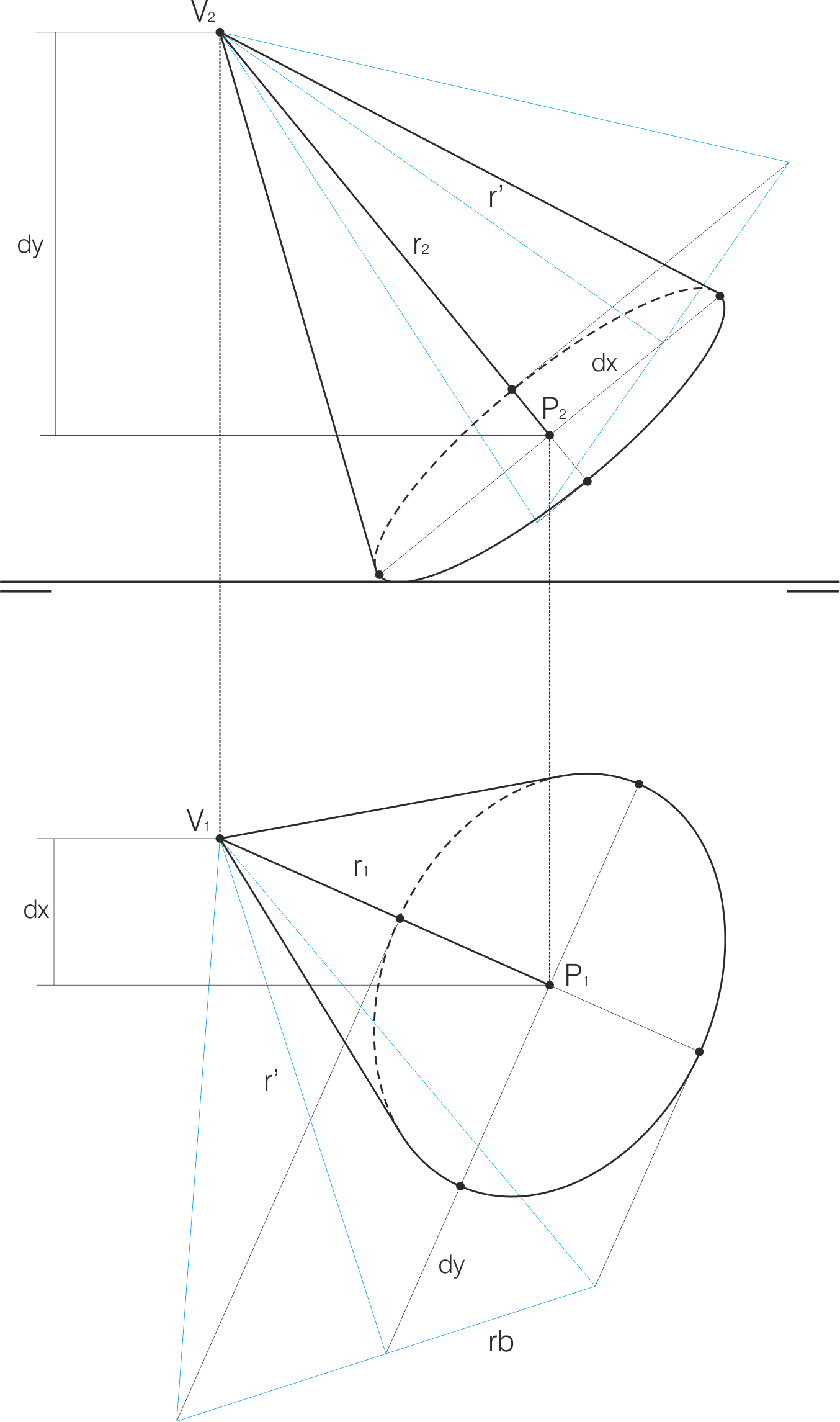
Si el eje del cono no se encuentra en una recta frontal u horizontal podemos abatir el plano que contiene a la base, encontrar su figura en verdadera magnitud y desabatirla. Pero si el cono es recto y de revolución podemos encontrar las proyecciones de la base mediante una construcción auxiliar, que por comodidad puede ser un abatimiento del eje (aunque ser un también un giro o un cambio de plano, como en el caso anterior).

Habitualmente se abate el eje (r) del cono para colocarlo frontal y horizontal (en ambas proyecciones), y sobre el eje girado se encuentran fácilmente los ejes de la elipse base, sabiendo que vemos el radio de la base (rb) en una perpendicular, en verdadera longitud.

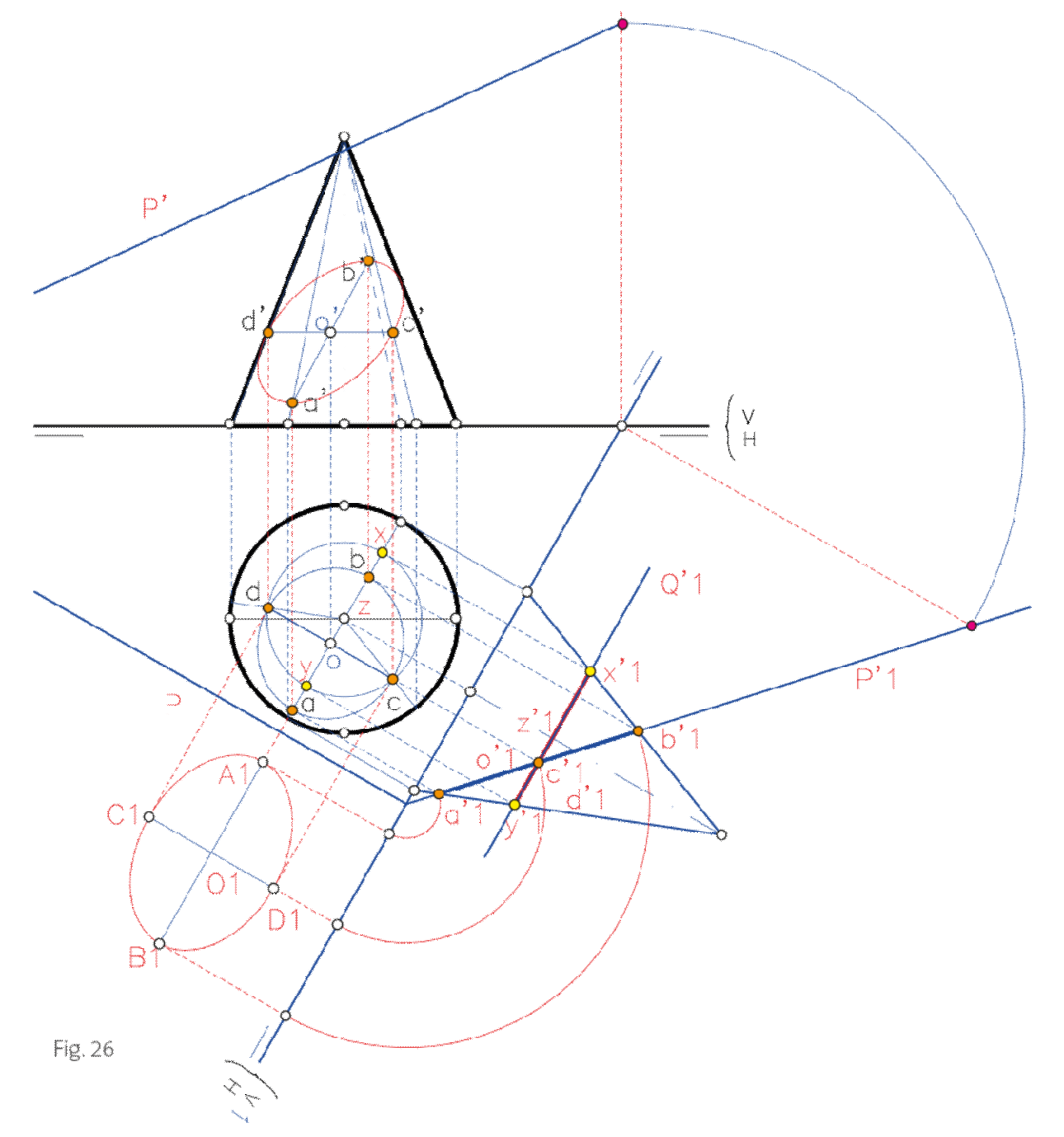
Intersección de recta y cono

Para resolver la intersección de una recta y un cono, podemos seguir dos métodos, de igual forma que se hacía en el caso de las pirámides:

Contener la recta en un plano auxiliar proyectante, cortar éste con el cono (obtenemos una cónica) y cortando la recta con esta figura. Este método no es preciso, ya que no dispondremos del trazado exacto de la curva intersección.

Contener la recta en un plano auxiliar que además pase por el vértice. La traza horizontal de este plano cortará a la base en dos puntos, que definen dos generatrices. Las dos generatrices y el segmento definido en la base por la intersección de ésta con la traza del plano definen el triángulo intersección, que a su vez se corta con la recta en los puntos buscados (los cortes de las dos generatrices con la recta son esos puntos).

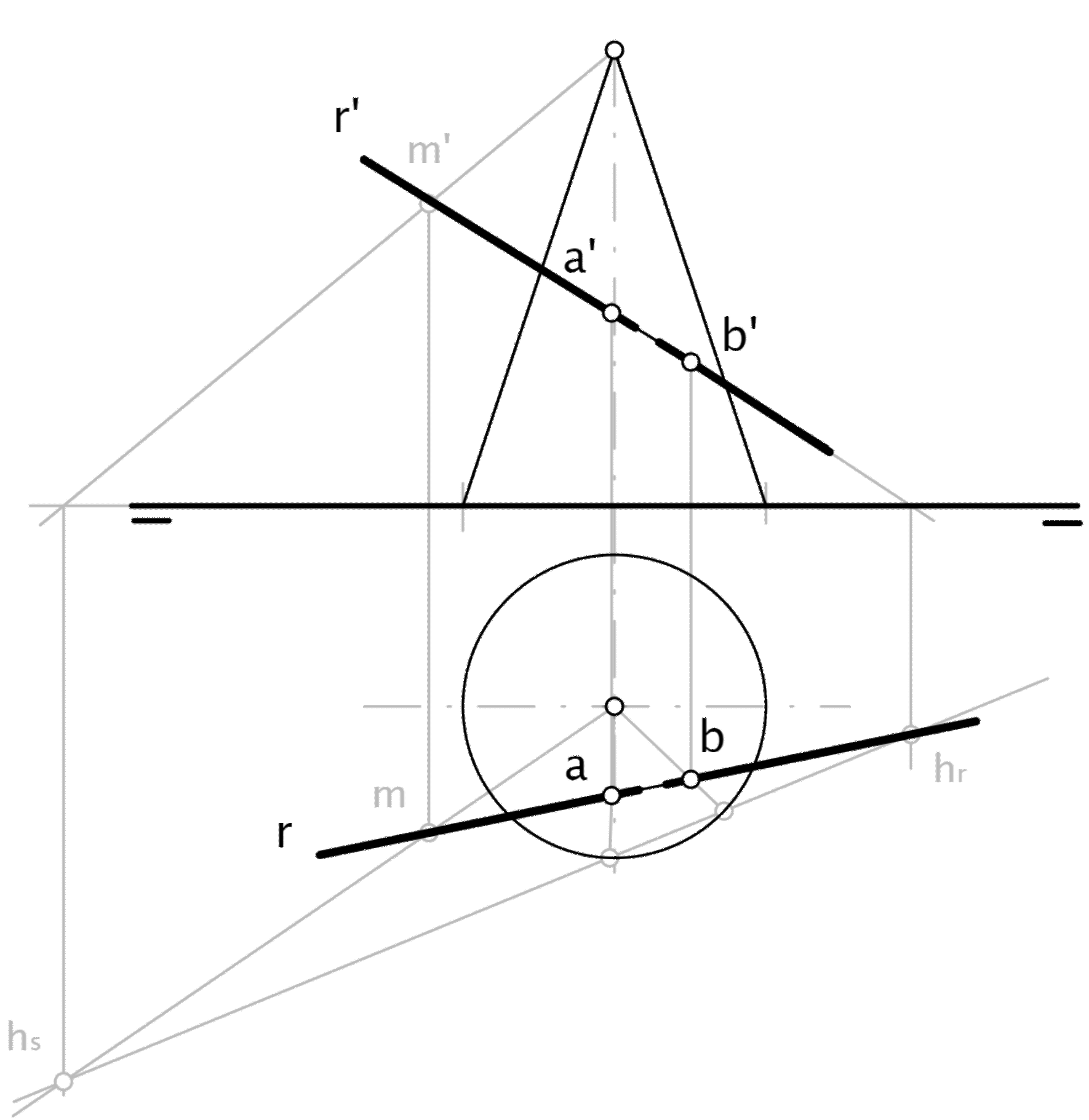
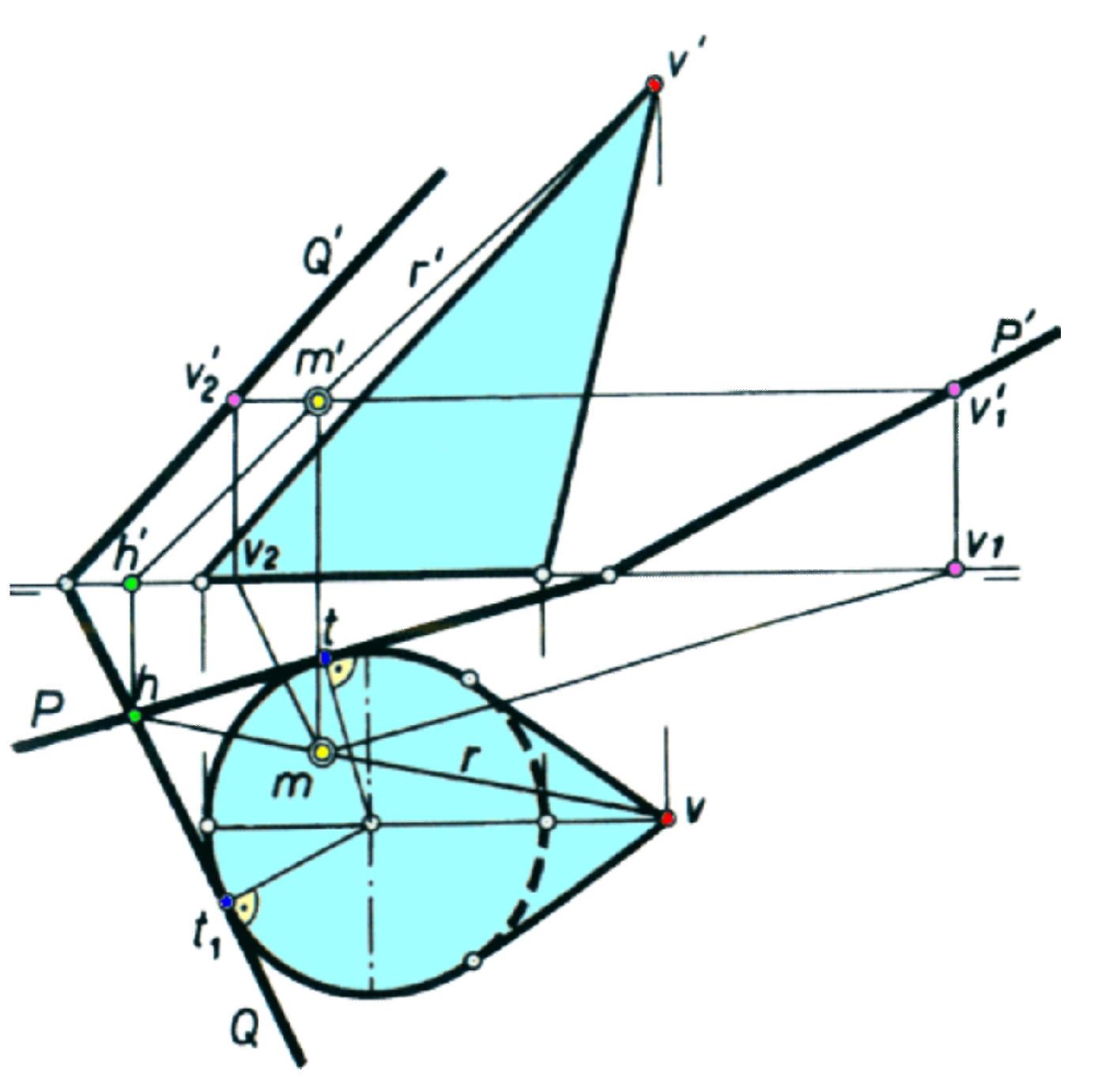
Plano tangente a un cono

Si un plano es tangente a un cono, contiene a una de sus generatrices (y, naturalmente, pasa por el vértice). Si además la base del cono está en H, la traza horizontal del plano será tangente a la proyección horizontal de la base en el pie de dicha generatriz.

Para encontrar un plano tangente a un cono por un punto de su superficie, basta con trazar la generatriz que contiene al punto, que proporcionará el punto de tangencia en la base (si la base es una elipse, para trazar la tangente a ella existe un método gráfico que podemos ver en el capítulo dedicado a la elipse).

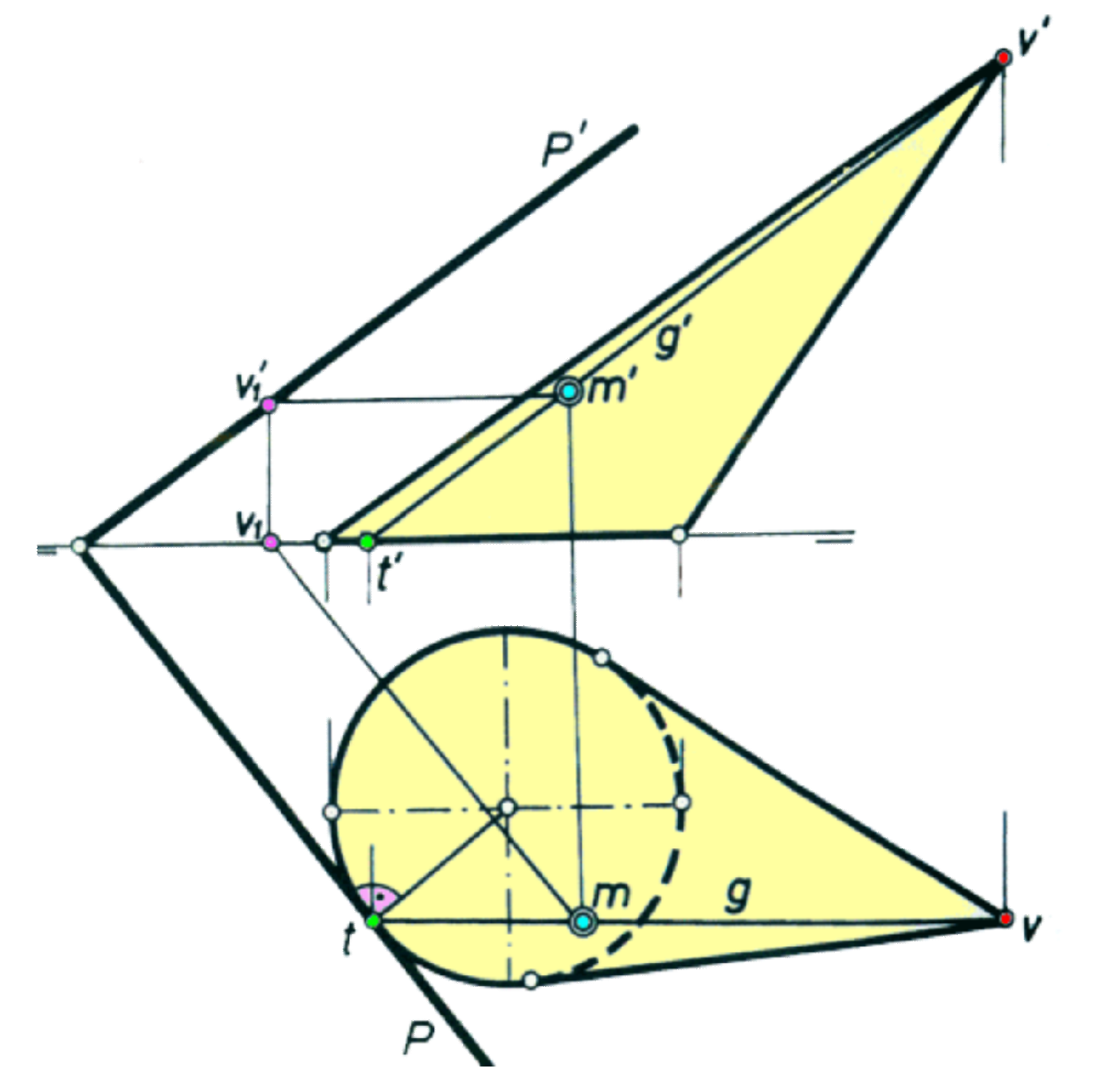
Para encontrar los planos paralelos a una dirección dada, trazamos por V una recta con esta dirección, operando de igual forma.

Desarrollo del cono y Transformada de la sección

El desarrollo de la superficie curva de un cono de revolución es un sector circular, de radio igual a la longitud de la generatriz. Para encontrar su ángulo de apertura, primero calculamos la longitud de la base (si no podemos hacerlo algebraicamente, lo hacemos mediante una rectificación). Sabiendo el radio del sector y la longitud del arco podemos obtener su ángulo de apertura.

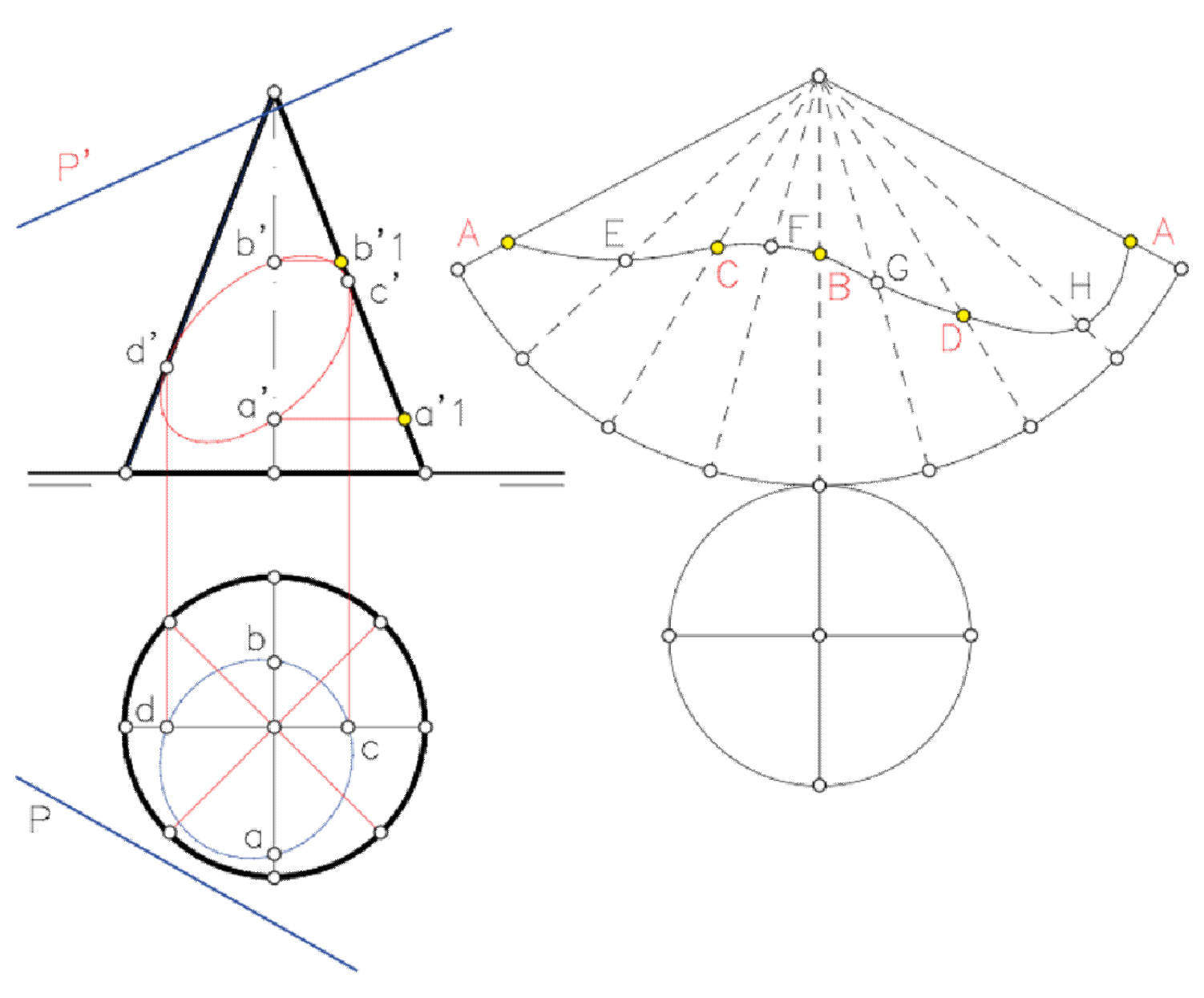
Si el cono es oblicuo, para desarrollarlo debemos dividir la base en trozos de igual longitud (longitud que deberemos rectificar) y trazar por los puntos de división las generatrices. Con las longitudes de estas generatrices y la de los trozos construimos triángulos, que serán una aproximación del desarrollo. Cuantas más divisiones hagamos, mejor será la aproximación.