Intersección de dos rectas

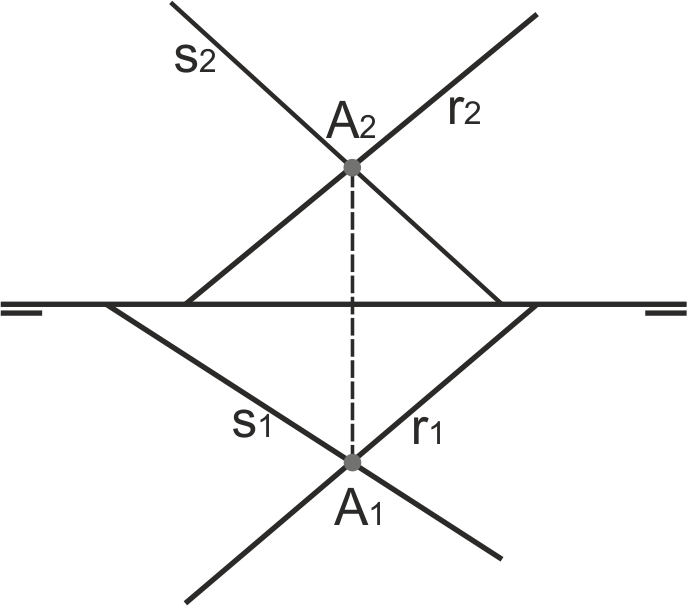
En capítulos anteriores ya hemos visto que la intersección de dos rectas que se cortan en el espacio es un punto, cuyas proyecciones son a su vez las intersecciones de las trazas de las rectas.

Intersección de dos planos

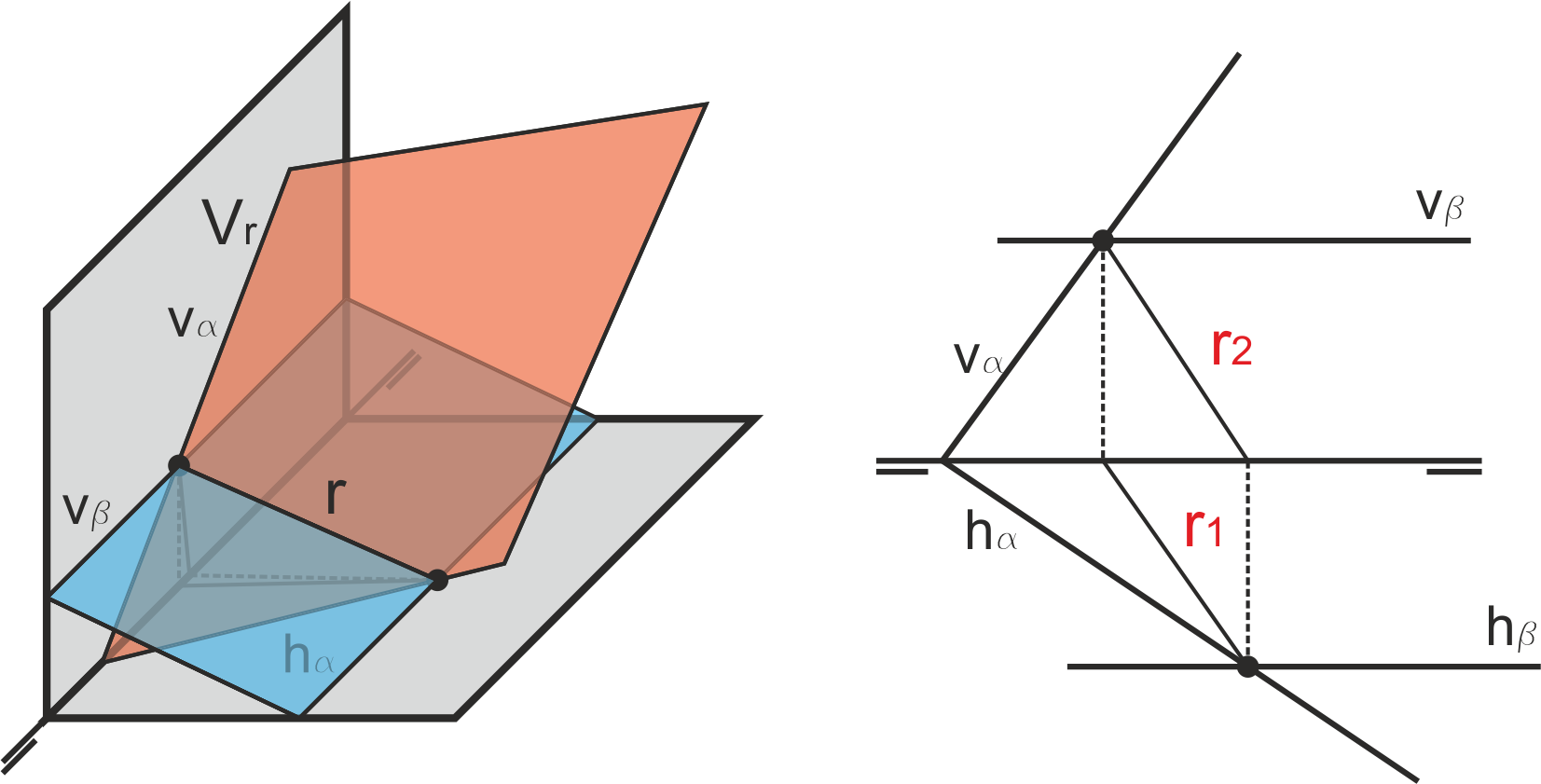
La intersección de dos planos no paralelos es una recta. Como las trazas de una recta están sobre las del plano, si la recta pertenece a ambos planos, sus trazas estarán simultáneamente sobre las de los dos planos. O lo que es lo mismo, las trazas de la recta intersección son las intersecciones de las trazas de los planos dos a dos.

Si uno de los planos es horizontal, la recta resultante es una horizontal del otro plano. Análogamente, si uno de los planos es frontal (figura de la derecha), la recta resultante es una frontal del otro plano.

Si uno de los planos es paralelo a la LT, la construcción es la misma.

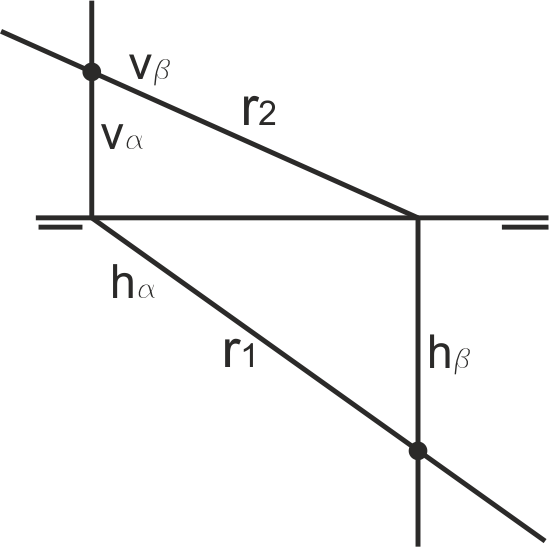
Si uno de los planos es proyectante vertical y el otro es proyectante horizontal, las proyecciones de la recta intersección coinciden con las trazas de los planos (figura de la derecha).

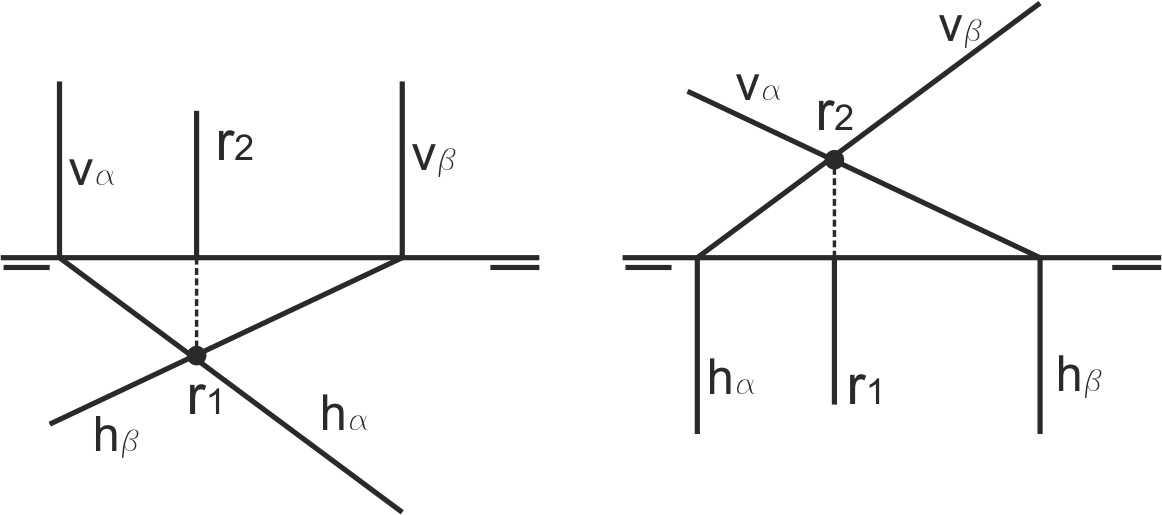
Si ambos planos son proyectantes horizontales, la intersección es una recta vertical, y si ambos planos son proyectantes verticales, la intersección es una recta de punta.

Si ambos planos son paralelos a la LT, la recta intersección debe encontrarse mediante una vista auxiliar de perfil.

Si uno de los dos planos es de perfil, también es necesaria una vista de perfil, ya que la solución será una recta de perfil (de la que tendremos que dar sus trazas o dos puntos que la definan).

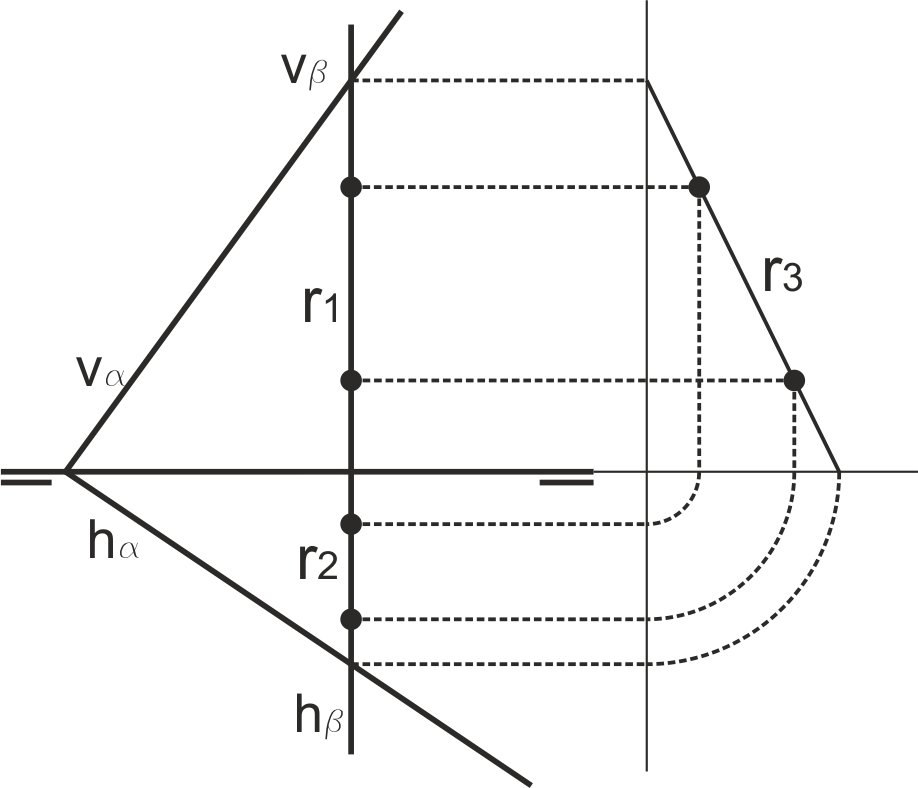
Si existen trazas paralelas (solo una de ellas, ya que de ser las dos paralelas los planos no se cortarán – serían paralelos), la intersección es una recta horizontal o frontal, con una de las proyecciones paralela a las trazas paralelas. En la figura de abajo se muestran ambos casos.

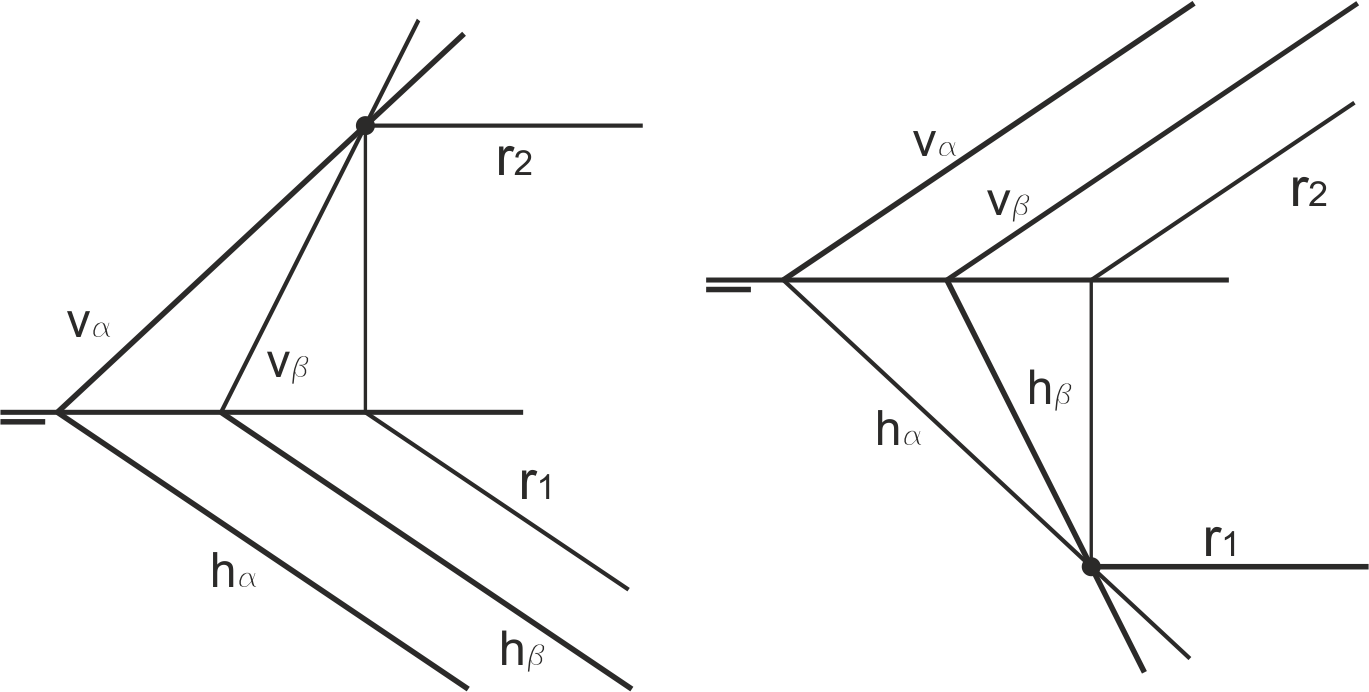
La recta de corte de un plano con el primer bisector tiene un punto en el vértice del plano. Para encontrar un segundo punto, basta con tomar una horizontal (o frontal) del plano y, en ella, encontrar un punto del primer bisector. Para cortar un plano con el segundo bisector realizamos la misma operación, pero encontrando un punto del segundo bisector. En ambos casos puede comprobarse que la recta solución cumple la pertenencia a BI o a BII.

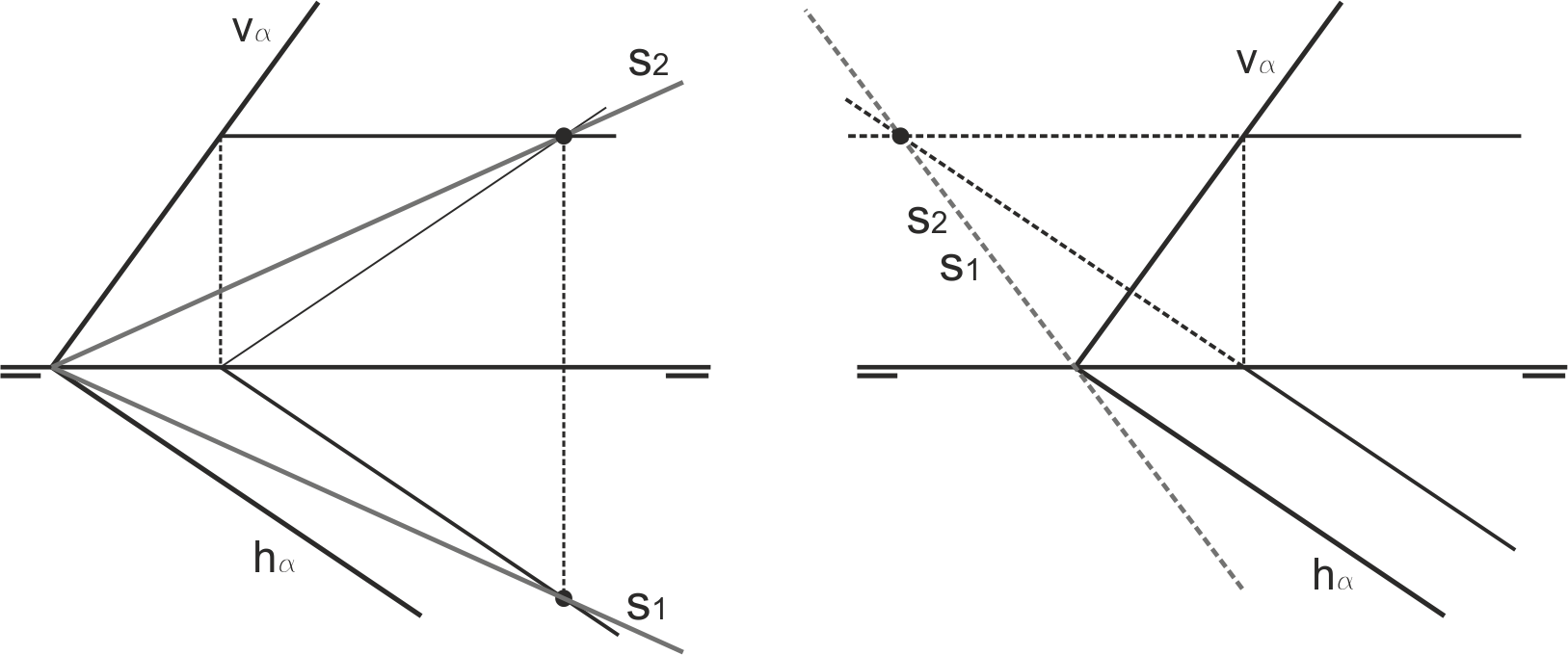
Si uno de los planos pasa por la LT, el vértice del plano es un punto de la recta buscada. En el ejemplo, el plano β que pasa por la LT viene definido por el punto A. Para encontrar un el segundo de la recta solución, tomamos una horizontal cualquiera s del plano α, y la cortamos con el plano β, obteniendo el punto B.

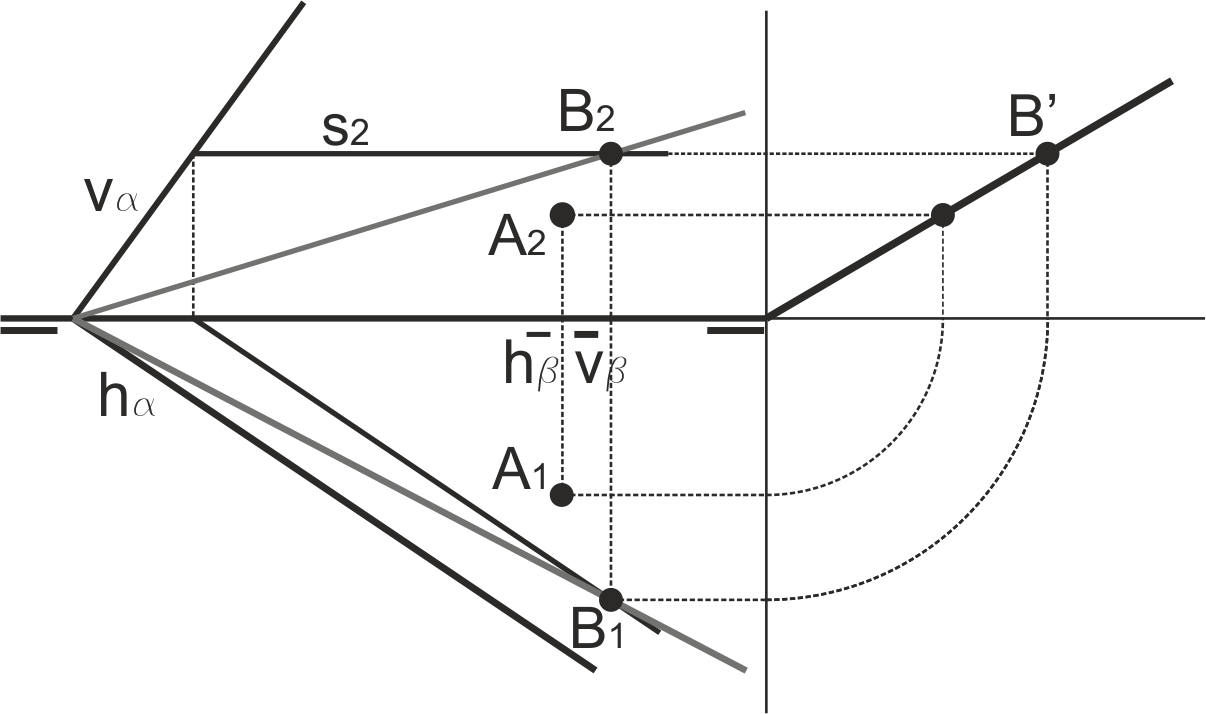
Si un par de trazas de los planos se cortan fuera de la zona de dibujo, solo disponemos de un punto de la solución (el corte de las trazas que sí se cortan en el papel). En este caso hay que tomar un tercer plano auxiliar horizontal o frontal que corte a las trazas que no se tocan (ϕ en la figura), con el que cortaremos ambos planos, obteniendo dos rectas (s y t en la figura). El corte de estas dos rectas nos dará el segundo punto de la solución buscada.

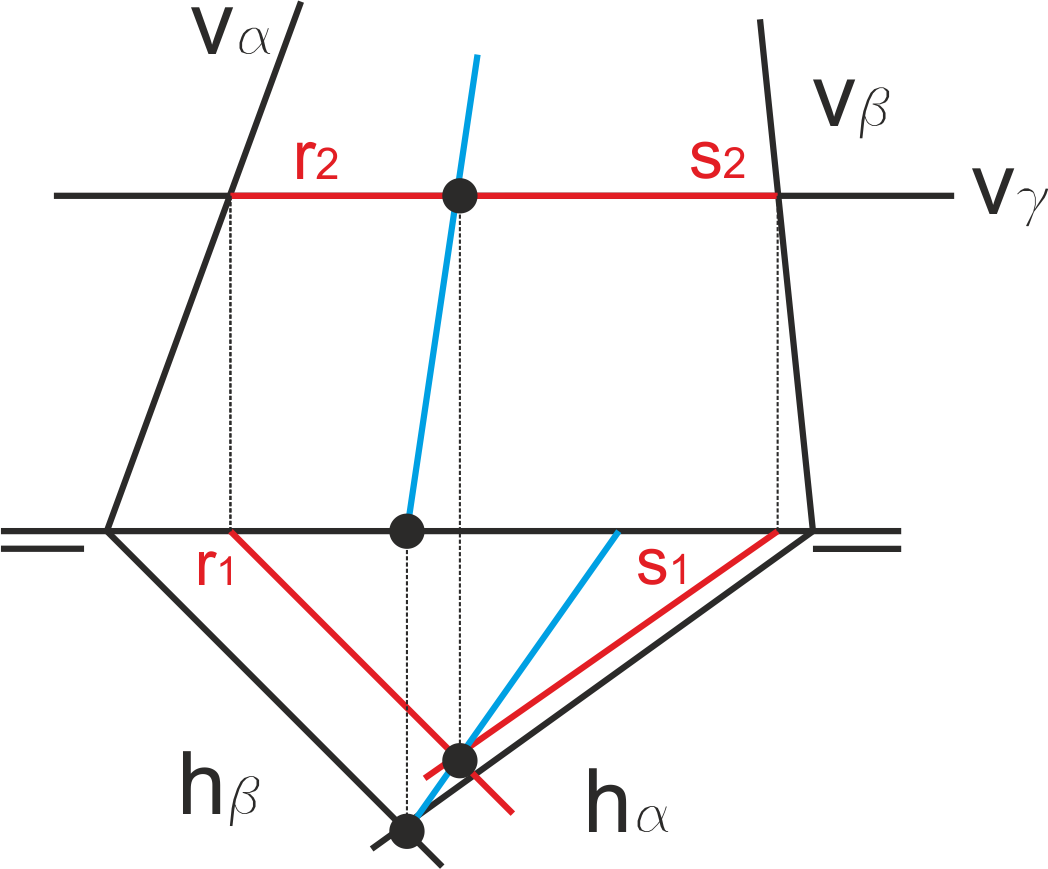
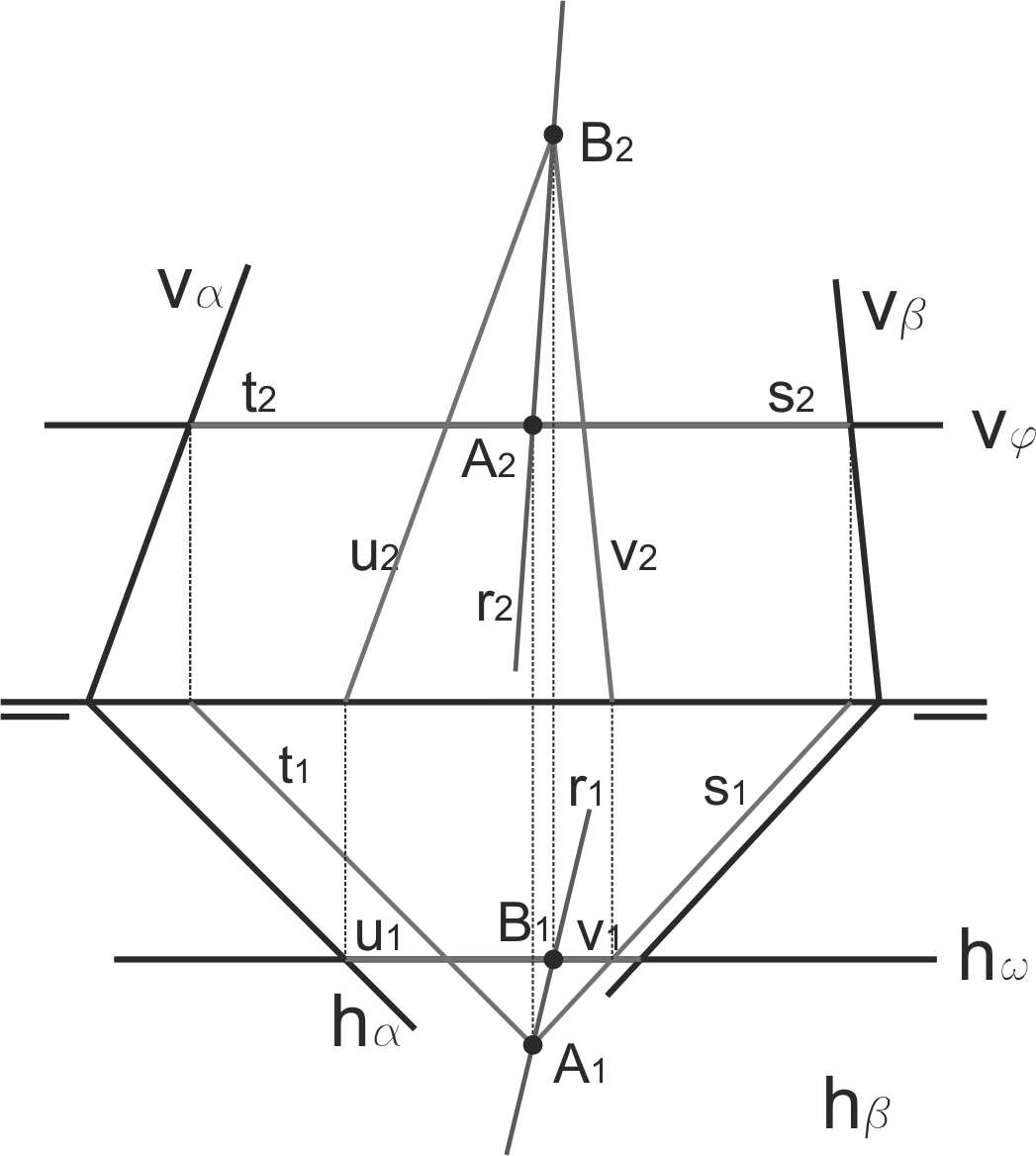
Si ninguno de los pares de trazas se corta en el papel, hay que tomar dos planos auxiliares, uno horizontal y otro frontal. Cada uno de ellos, al cortarse con los planos, proporciona un punto.

En el ejemplo de la izquierda, hemos tomado el plano ϕ horizontal que corta a los planos α y β en las rectas s y t, que a su vez se cortan en el punto A. El plano ω frontal corta a los planos α y β en las rectas u y v, que a su vez se cortan en el punto B. La solución r buscada es la que pasa por A y B.

Intersección de recta y plano

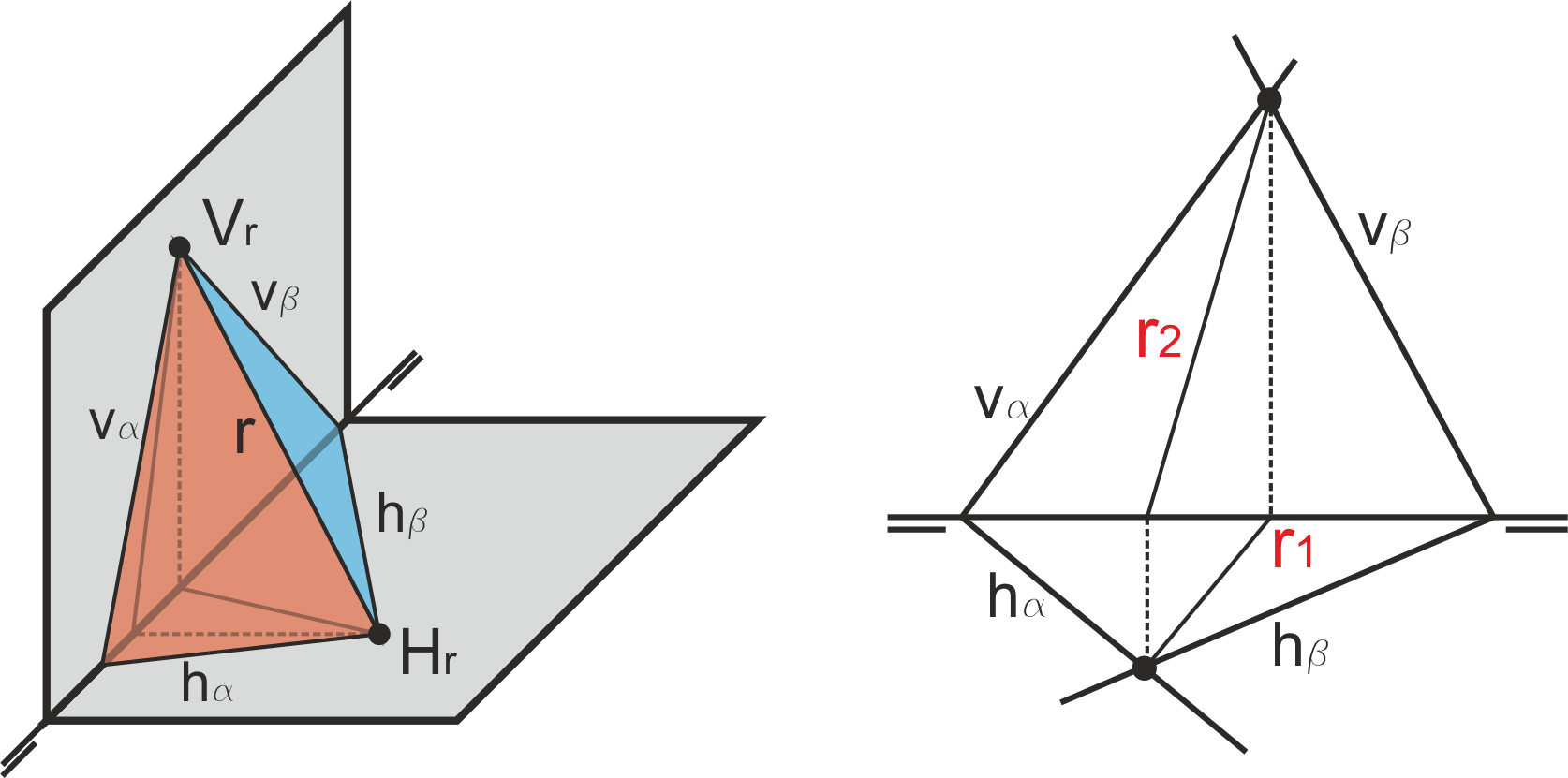
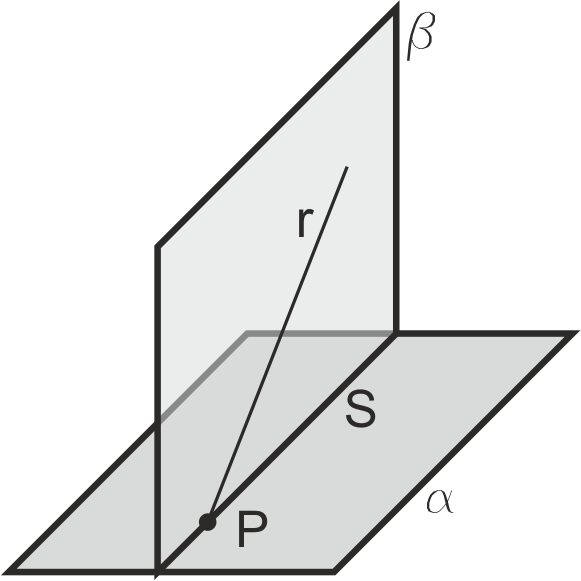
No existe ninguna construcción directa en diédrico para obtener la intersección (P) entre un plano (α) y una recta (r). Para realizarla, necesitamos tomar un plano auxiliar (β en la figura) que contenga a la recta r, al que cortaremos con el otro plano. La recta s intersección de ambos se cortará con r en P, el punto buscado.

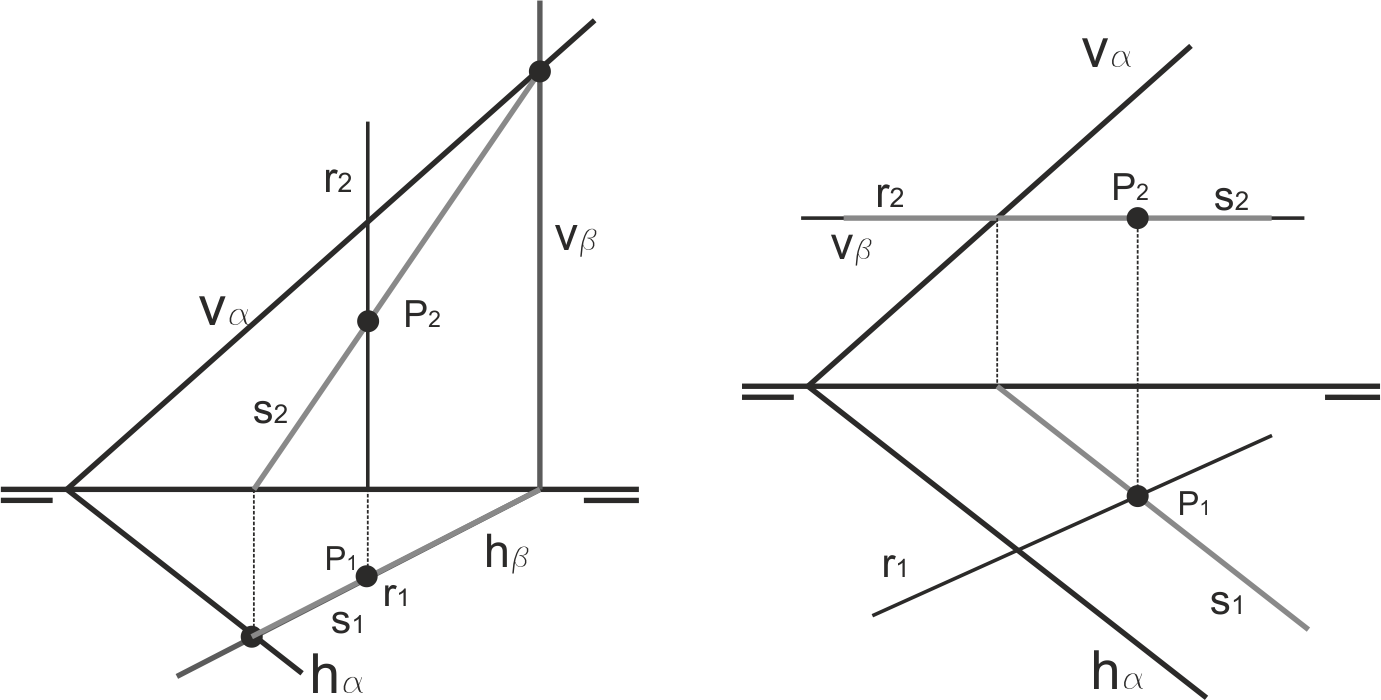
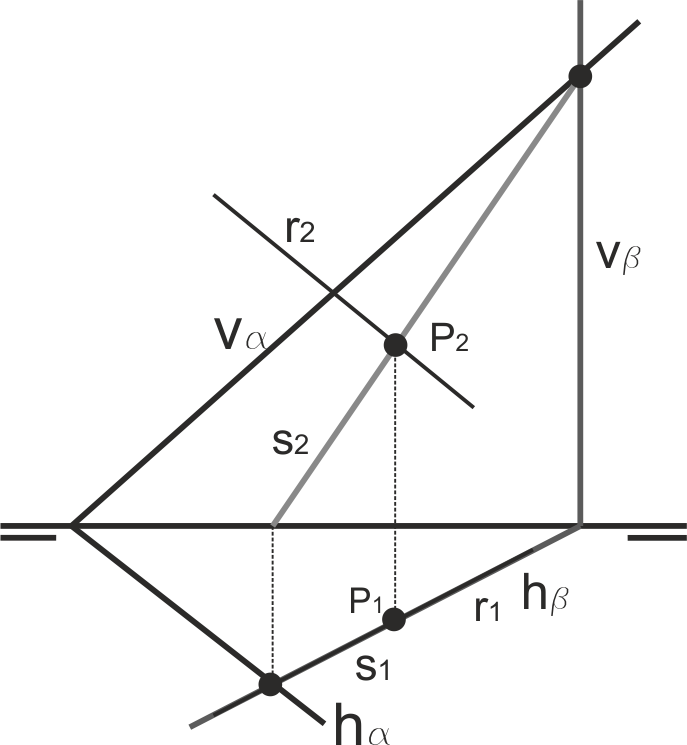
Por comodidad, este plano auxiliar se suele tomar como proyectante horizontal o proyectante vertical. En la figura, hemos tomado un plano β proyectante vertical que contiene a r. La proyección s2 se corta con r2 en P2, proyección vertical del punto P buscado.

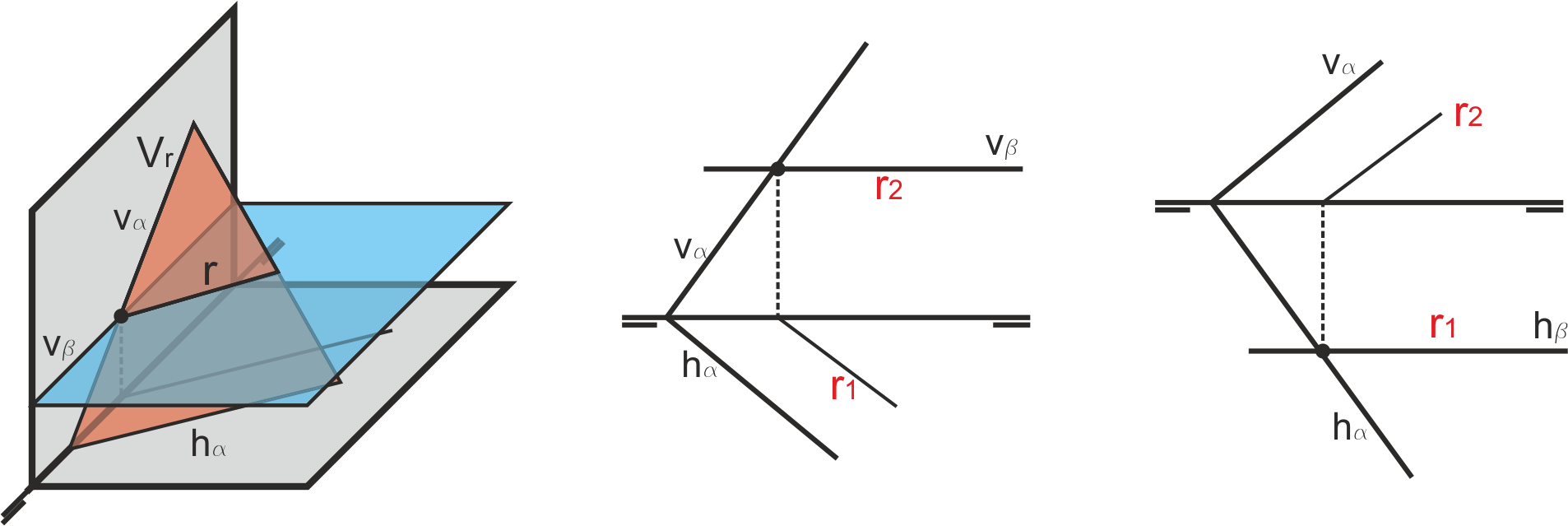
En la figura de la izquierda siguiente, la recta a cortar con el plano es vertical, pero el procedimiento es idéntico. El plano auxiliar elegido en este caso también es proyectante vertical. En la figura de la derecha la recta r es horizontal, y el plano proyectante vertical que la contiene es un plano horizontal (aunque podría haberse resuelto igualmente tomando un plano proyectante horizontal).